
- •3.4 Компоновка оптической системы……………………………….…. 25
- •Введение.
- •2. Теория телескопической системы.
- •2.1 Общие положения теории телескопических систем.
- •2.2 Особенности телескопа (зрительной трубы) Кеплера.
- •2.3 Основные компоненты телескопической системы.
- •2.3.1 Окуляры.
- •2.3.2 Объективы.
- •2.3.3 Отражательные призмы.
- •2. Призмы с двумя отражающими гранями всегда дают прямое изображение.
- •2.3.4 Линзовые оборачивающие системы.
- •2.4. Допустимые значения аберраций в телескопических системах.
- •Габаритный расчет оптической системы:
- •3.1. Выбор и расчет окуляра.
- •3.2. Выбор и расчет объектива.
- •3.3 Выбор и расчет призменной оборачивающей системы.
- •3.4 Компоновка оптической системы
- •4. Аберрационный расчет всей системы.
- •5. Расчет коэффициента пропускания зрительной трубы
- •6. Расчет изменений параметров при изменении температуры окружающей среды.
- •7. Расчет подвижки объектива при работе на 20 метров.
- •8. Заключение.
- •9. Список используемой литературы:
Содержание:
Введение………………………………………………………………………….. 4
Теория телескопической системы……………………………………...……… 4
2.1 Общие положения теории телескопических систем……………….….. 4
2.2 Особенности телескопа (зрительной трубы) Кеплера………………… 6
2.3 Основные компоненты телескопической системы……………………. 10
2.3.1 Окуляры……………………………………………………………….. 10
2.3.2 Объективы…………………………………………………………….. 15
2.3.3 Отражательные призмы…………………………………………….. 17
2.3.4 Линзовые оборачивающие системы……………………………….. 19
2.3.5 Допустимые значения аберраций в телескопических системах.. 19
Габаритный расчет оптической системы:……………………………………. 21
3.1 Выбор и расчет окуляра…………...………………………………… 22
3.2 Выбор и расчет объектива.………………………………………….. 23
3.3 Выбор и расчет призменной оборачивающей системы ……..….. 25
3.4 Компоновка оптической системы……………………………….…. 25
4. Аберрационный расчет всей системы…………………………………………. 26
5. Расчет коэффициента пропускания зрительной трубы …………………….. 26
6. Расчет изменений параметров при изменении температуры окружающей среды.………………………………………………………………………………. 27
7. Расчет подвижки объектива…………………………………………………….. 30
8. Заключение. 31
9. Список используемой литературы……………………………………………... 32
10. Приложение №1………………………………………………………………….. 33
Введение.
Курсовая работа выполняется с целью изучения простой телескопической системы и ее основных оптических характеристик; получения навыков проведения габаритного расчета, компьютерного проектирования и оценки качества изображения оптических систем указанного типа. В процессе выполнения курсовой работы необходимо решить следующие задачи:
1) провести габаритный расчет телескопической системы, построенной по схеме Кеплера в соответствии с исходными данными;
2) осуществить выбор компонентов системы из архивов оптических систем и компоновку схемы;
3) провести проверочные расчеты телескопических систем по программам автоматизированного расчета оптики и проанализировать параксиальные и аберрационные характеристики полученных систем;
4) провести расчет изменений параметров и аберраций зрительной трубы при изменении температуры окружающей среды на ±40 С
5) определить коэффициент пропускания оптической системы и произвести другие расчеты, представленные в данном курсовом проекте.
2. Теория телескопической системы.
2.1 Общие положения теории телескопических систем.
Телескопические системы (зрительные трубы) - наиболее распространенная группа оптических систем. Телескопические системы являются основной частью многих оптических приборов: геодезических, астрономических, наблюдательных, угломерных, дальномеров, прицелов.
Телескопическая система предназначена для наблюдения далеких предметов. Диаметр входного зрачка телескопической системы всегда мал по сравнению с расстоянием до наблюдаемого предмета, т.е. мал ее передний апертурный угол. В большинстве случаев можно считать, что передний апертурный угол телескопической системы равен нулю и во входной зрачок системы входят параллельные пучки лучей.
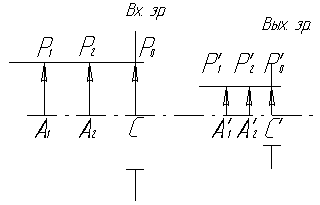
Рис. 2.1.1
Телескопическая система - визуальный прибор. Если глаз наблюдателя эмметропический и его дальняя точка лежит на бесконечности, то для устранения утомления глаза напряжением аккомодации необходимо, чтобы создаваемое телескопической системой и рассматриваемое глазом изображение предмета находилось на бесконечности. Поэтому задний апертурный угол телескопической системы также близок к нулю, и можно считать, что ее выходкой зрачок покидают параллельные пучки лучей.
На рис. 2.1.1 показаны входной и выходной зрачки телескопической системы, центры которых лежат в точках С и С´. Пусть в пространстве предметов имеется луч Р1Р0, идущий от осевой точки бесконечно удаленного предмета, а в пространстве изображений - сопряженный с ним луч Р´1Р´0, направляющийся к осевой точке бесконечно удаленного изображения. Оба луча параллельны оптической оси системы.
Рассмотрим предмет А1Р1=у, нижний конец которого лежит на оптической оси, а верхний - на луче Р1Р0. В пространстве изображений должно существовать изображение А´1Р´1= у´ этого предмета, при этом его концы А´1 и Р´1 должны лежать, соответственно, на оптической оси и па луче Р´1Р´0 . Линейное увеличение для этого положения предмета:
![]() . (2.1.1)
. (2.1.1)
Передвинем предмет у в новое положение А2Р2 таким образом, чтобы его концы оставались соответственно на оптической оси и на луче Р1Р0. При этом изображение у´ переместится в некоторое положение А´2Р´2- причем точка А´2 будет лежать на оптической оси, а точка Р´2 - на луче Р´1Р´0. Вследствие этого и величина у´ изображения также останется неизменной, а потому не изменится и линейное увеличение V. Таким образом, линейное увеличение телескопической системы не зависит от положения предмета. Мы можем поместить предмет CР0 = у во входном зрачке системы. Тогда его изображение предмет C´Р´0 = у´ будет находиться в выходном зрачке, но величины у и у´ будут теми же самыми. Вследствие этого линейное увеличение Vc в зрачках телескопической системы будет равно его постоянному линейному увеличению V:
![]() .
(2.1.2)
.
(2.1.2)
Угловое увеличение W любой оптической системы связано с линейным увеличением V формулой:
![]() . (2.1.3)
. (2.1.3)
Как и линейное увеличение, угловое увеличение телескопической системы не зависит от положения предмета:
![]() . (2.1.4)
. (2.1.4)
Продольное увеличение Q и продольное увеличение в точке q:
![]() . (2.1.5)
. (2.1.5)
Таким образом, и продольное увеличение телескопической системы не зависит от положения предмета.
Видимое увеличение Г любой оптической системы определяется формулой:
![]() . (2.1.6)
. (2.1.6)
Поскольку мы сейчас рассматриваем системы дальнего действия, можем стать величины p и k равными. Равными можно считать и отрезки р´ и к´, так как зрачок глаза совпадает с выходным зрачком телескопической системы или удален от него на расстояние, малое по сравнение с самими отрезками р´ и к´. Поэтому
![]() . (2.1.7)
. (2.1.7)
Таким образом, линейное, угловое, продольное и видимое увеличения телескопической системы постоянны, независимо от положения предмета. Выразим через видимое увеличение телескопической системы все остальные ее увеличения:
![]() (2.1.8)
(2.1.8)
Если пространства предметов и изображений находятся воздухе (n´=n=1) получим:
![]() (2.1.9)
(2.1.9)
Вследствие того, что линейное и продольное увеличения не равны между собой, происходит искажение видимого через телескопическую систему пространственного оптического изображения. Если, как это обычно бывает, Г >1, то Q< V, и пространственное изображение будет представляться сплюснутым вдоль оптической оси прибора. При большом увеличении телескопической системы эта сплюснутость легко обнаруживается.
И
Рис. 2.1.2
Рис. 2.1.2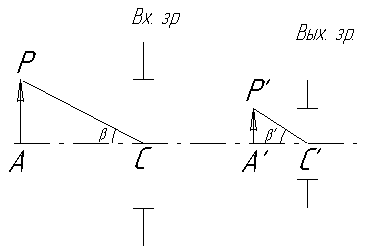 елескопической
системы (рис. 2.1.2). Наблюдатель, зрачок
глаза которого находится у выходного
зрачка трубы, видит изображение А´Р´
на расстоянии А´C´
от выходного зрачка.
Отрезок А´Р´ в
Г раз меньше
АР. Но, в то
же время, отрезок А´С´ в
Г² раз меньше
отрезка АС.
Поэтому тангенс угла β,
под которым вооруженный телескопом
глаз видит изображение, в Г
раз больше тангенса угла β,
под которым невооруженный глаз видит
предмет, что и
елескопической
системы (рис. 2.1.2). Наблюдатель, зрачок
глаза которого находится у выходного
зрачка трубы, видит изображение А´Р´
на расстоянии А´C´
от выходного зрачка.
Отрезок А´Р´ в
Г раз меньше
АР. Но, в то
же время, отрезок А´С´ в
Г² раз меньше
отрезка АС.
Поэтому тангенс угла β,
под которым вооруженный телескопом
глаз видит изображение, в Г
раз больше тангенса угла β,
под которым невооруженный глаз видит
предмет, что и
