1. Дан закон распределения дискретной случайной величины X:

Н

X	–2	–1	1	2
P	0,4	0,1		0,3

айти: 1) значение вероятности , соответ-

ствующее значению ;

2) , , ;

3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.

2. Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .

3. Производится серия независимых испытаний, в каждом из которых событие A появляется с вероятностью . Рассматривается случайная величина X – число появлений события A в серии из испытаний. Составить закон распределения вероятностей, многоугольник и функцию распределения вероятностей случайной величины X. Найти математическое ожидание и дисперсию .

4. Дискретная случайная величина распределена по закону Пуассона вероятностей массовых (n – велико) и редких (p – мало) событий , . Найти математическое ожидание и дисперсию этой случайной величины.

5. Производится ряд выстрелов из орудия с вероятностью попадания . Стрельба ведется до первого попадания, но не свыше выстрелов. Найти функцию распределения случайной величины X – числа выстрелов, производимых орудием до первого попадания. Найти вероятность того, что будет сделано не менее одного, но меньше 3-х выстрелов. Определить среднее значение числа произведенных выстрелов и примерный расход снарядов на 100 подобных стрельб.

6. Непрерывная случайная величина X задана плотностью вероятности

Н

айти: 1) функцию распределения ;

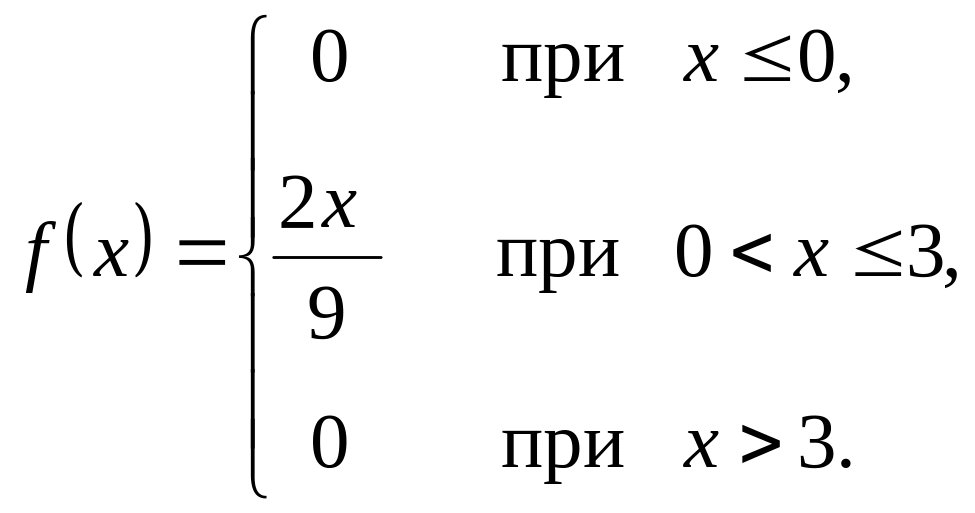
2) , , ;

3) вероятность того, что в результате

опыта случайная величина X примет

значение, принадлежащее интервалу . Построить графики функций и .

7. Автобусы некоторого маршрута идут строго по расписанию с интервалом движения 8 мин. Найти вероятность того, что пассажир, пришедший к остановке, будет ожидать очередной автобус менее 3-х мин.

8. Непрерывная случайная величина X распределена по показательному закону 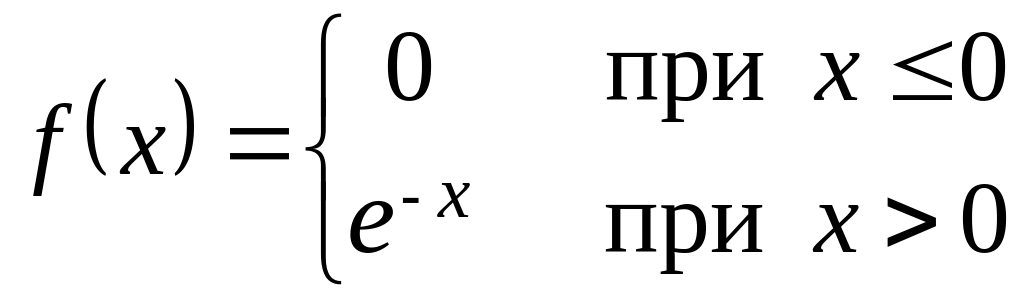. Найти математическое ожидание и дисперсию случайной величины X. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале .

9. Непрерывная случайная величина X распределена по нормальному закону . Найти , . Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале .

10. Случайная величина X распределена нормально с математическим ожиданием и средним квадратическим отклонением . Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 попадет величина X в результате испытания.

11. Сколько следует проверить деталей, чтобы с вероятностью, не меньшей 0,95, можно было утверждать, что абсолютная величина отклонения частоты годных деталей от вероятности детали быть годной, равной 0,9, не превысит 0,01?

12. Сколько измерений надо сделать, чтобы среднее арифметическое дало измеряемую с точностью до 0,05 и надежностью 90%, если дисперсии случайных величин (результатов измерений) равны 0,2.

13. Система двух случайных величин подчиняется нормальному закону с плотностью вероятности . Определить вероятность совместного выполнения двух неравенств: , .

В а р и а н т 16