
- •Варианты контрольных работ по теме «Случайные величины»
- •. Непрерывная случайная величина X распределена по нормальному закону . Найти , . Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Непрерывная случайная величина X распределена по нормальному закону . Найти , . Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Непрерывная случайная величина X распределена по нормальному закону . Найти , . Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Непрерывная случайная величина X распределена по нормальному закону . Найти , . Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
- •Дан закон распределения дискретной случайной величины X:
- •3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
- •Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
Дан закон распределения дискретной случайной величины X:
Н
X
1
2
3
4
P
0,1
0,4
0,3
ствующее значению ;
2) , , ;
3) Функцию распределения ; построить ее график. Построить многоугольник распределения случайной величины X.
Случайные величины X и y независимы. Найти математическое ожидание и дисперсию случайной величины , если , , , .
Производится серия независимых испытаний, в каждом из которых событие A появляется с вероятностью
 .
Рассматривается случайная величина
X
– число появлений события A
в серии из
.
Рассматривается случайная величина
X
– число появлений события A
в серии из
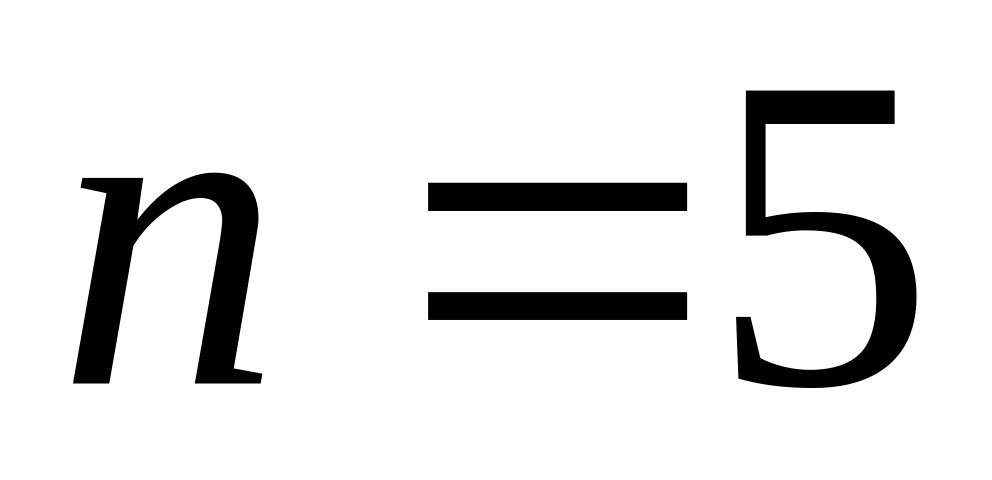 испытаний. Составить закон распределения
вероятностей, многоугольник и функцию
распределения вероятностей
случайной величины X.
Найти математическое ожидание
и дисперсию
.
испытаний. Составить закон распределения
вероятностей, многоугольник и функцию
распределения вероятностей
случайной величины X.
Найти математическое ожидание
и дисперсию
.Дискретная случайная величина распределена по закону Пуассона вероятностей массовых (n – велико) и редких (p – мало) событий
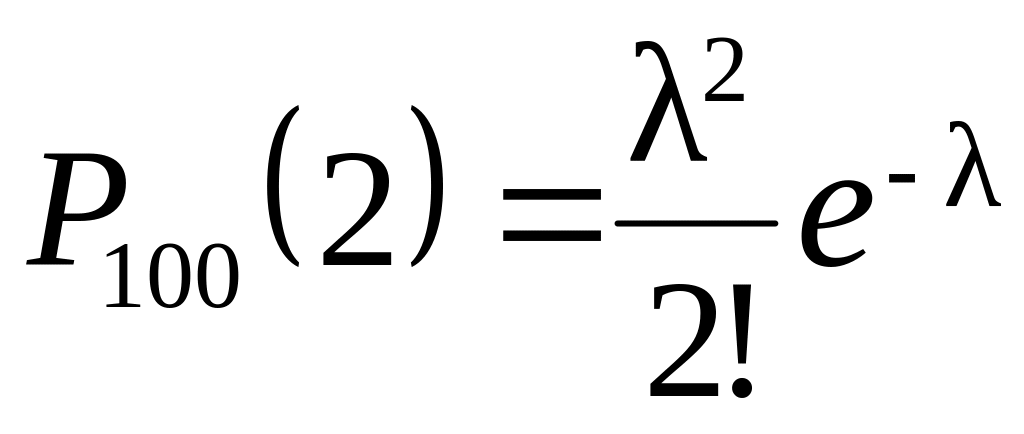 ,
,
 .
Найти математическое ожидание и
дисперсию этой случайной величины.
.
Найти математическое ожидание и
дисперсию этой случайной величины.Производится ряд выстрелов из орудия с вероятностью попадания . Стрельба ведется до первого попадания, но не свыше выстрелов. Найти функцию распределения случайной величины X – числа выстрелов, производимых орудием до первого попадания. Найти вероятность того, что будет сделано не менее одного, но меньше 5-ти выстрелов. Определить среднее значение числа произведенных выстрелов и примерный расход снарядов на 100 подобных стрельб.
Непрерывная случайная величина X задана плотностью вероятности
Н
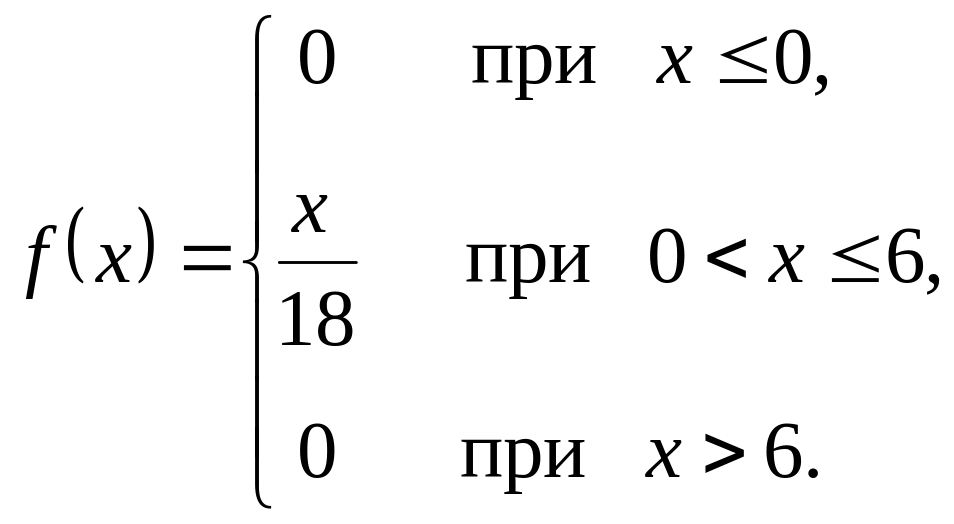
2) , , ;
3) вероятность того, что в результате
опыта случайная величина X примет
значение, принадлежащее интервалу . Построить графики функций и .
Цена деления шкалы амперметра равна 0,1 A. Показания округляются до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 A.
Непрерывная случайная величина X распределена по показательному закону с функцией плотности
 Найти математическое ожидание и
дисперсию случайной величины X.
Найти вероятность того, что в результате
испытания X
попадет в интервал
Найти математическое ожидание и
дисперсию случайной величины X.
Найти вероятность того, что в результате
испытания X
попадет в интервал
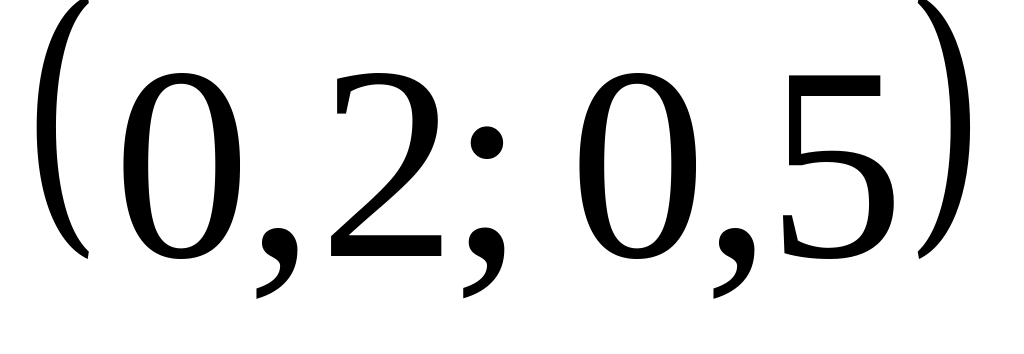 .
.Непрерывная случайная величина X распределена по нормальному закону . Найти , . Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале .
Случайная величина X распределена нормально с математическим ожиданием
 .
Вероятность попадания X
в интервал
.
Вероятность попадания X
в интервал
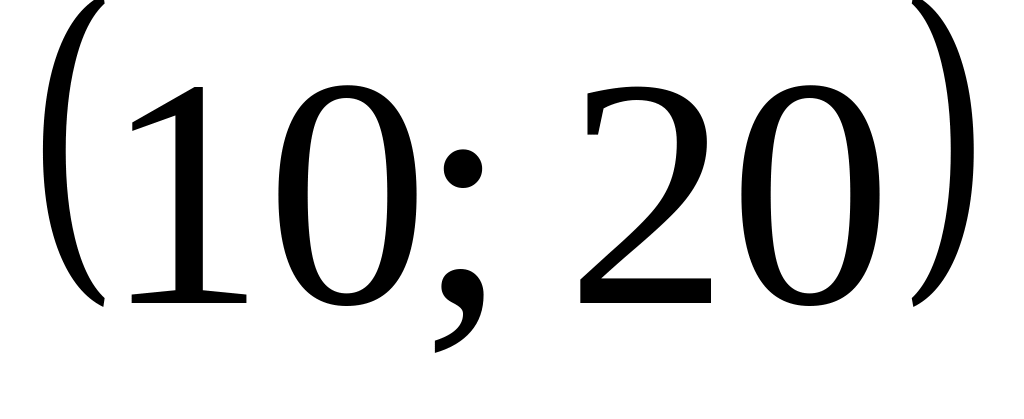 равна 0,3. Чему равна вероятность
попадания X
в интервал
?
равна 0,3. Чему равна вероятность
попадания X
в интервал
?Суточная потребность в электроэнергии в населенном пункте является случайной величиной, математическое ожидание которой равно 2000 квт/ч, а дисперсия составляет 20 000. Оценить вероятность того, что в ближайший день расход электроэнергии в этом населенном пункте будет от 1500 до 2500 кВт/ч.
Вероятность события A при каждом испытании равна 0,7. Сколько раз достаточно повторить испытания, чтобы с вероятностью 0,9 можно было ожидать, что частота появления события A будет отклоняться от вероятности не больше чем на 0,05?
Найти вероятность попадания случайной точки в прямоугольник, ограниченный прямыми
 ,
,
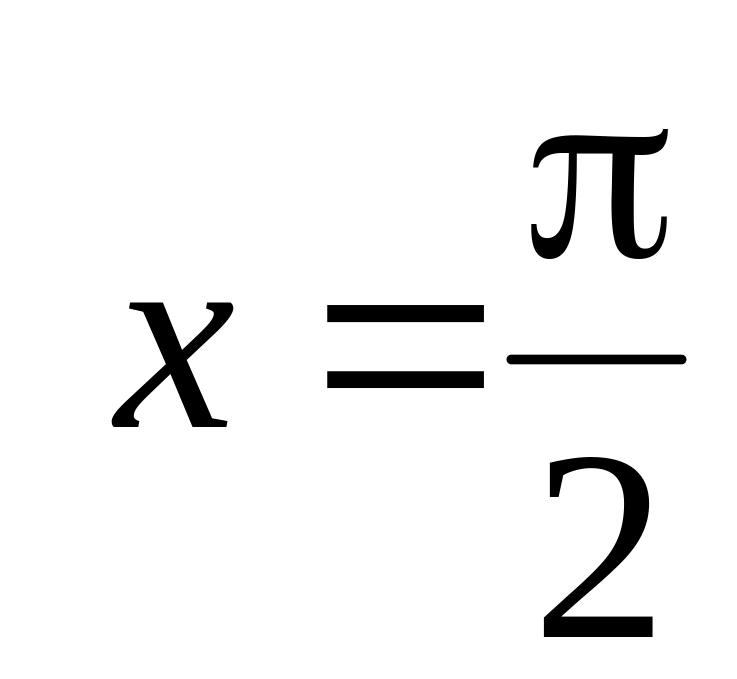 ,
,
 ,
,
 ,
если известна функция распределения
,
если известна функция распределения
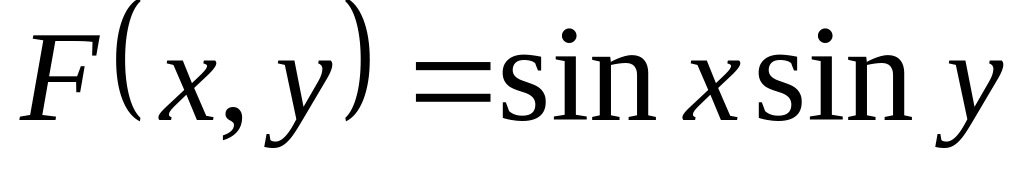
 .
.
В а р и а н т 12
