
- •Змістовий модуль 7 дослідження функцій з допомогою похідних
- •7.1 Дослідження функції за допомогою похідних
- •7.1.1. Деякі теореми про функції, що диференціюються
- •7.1.2. Правила Лопіталя
- •Розкриття невизначеностей різних видів
- •7.1.3. Зростання і спдання функцій
- •7.1.4. Максимум і мінімум функцій
- •7.1.5. Найбільше і найменше значення функції на відрізку
- •7.1.6. Опуклість графіка функції. Точки перегину
- •7.1.7. Асимптоти графіка функції.
- •7.1.8. Загальна схема дослідження функції і побудови графіка
- •7.2. Формула тейлора
- •7.2.1. Формула Тейлора для многочлена
- •7.2.2. Формула Тейлора для довільної функції
- •§7.3. Означення і представлення комплексних чисел
- •7.3.1. Основні поняття
- •7.3.2 Геометричне зображення комплексних чисел
- •Ф орми запису комплексних чисел
- •7.4. Дії над комплексними числами
- •7.4.1 Додавання комплексних чисел
- •Віднімання комплексних чисел
- •Множення комплексних чисел
- •Ділення комплексних чисел
- •Добування коренів з комплексних чисел
§7.3. Означення і представлення комплексних чисел
7.3.1. Основні поняття
Комплексним
числом
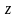 називається
вираз вигляду
називається
вираз вигляду
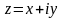 де х
і у
— дійсні числа, а і
— так звана уявна
одиниця
де х
і у
— дійсні числа, а і
— так звана уявна
одиниця
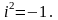
Якщо
х=0,
то число
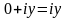 називається чисто уявним; якщо у=0,
то число
називається чисто уявним; якщо у=0,
то число
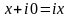 ототожнюється з дійсним числом х,
а це означає, що множина R
всіх дійсних чисел є підмножиною множини
С всіх комплексних чисел, т.е. R
ототожнюється з дійсним числом х,
а це означає, що множина R
всіх дійсних чисел є підмножиною множини
С всіх комплексних чисел, т.е. R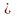 С
.
С
.
Число х називається дійсною частиною комплексного числа і позначається х=Re z, а у — уявною частиною z, y=Im z .
Два
комплексні числа
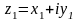 і
і
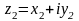 називаються рівними (z1=z2)
тоді і тільки тоді, коли рівні їх дійсні
частини і рівні їх уявні частини: x1=x2,
y1=y2
. Зокрема, комплексне число
рівно нулю тоді і тільки тоді, коли
x=y=0
. Поняття «більше» і «менше» для
комплексних чисел не вводяться.
називаються рівними (z1=z2)
тоді і тільки тоді, коли рівні їх дійсні
частини і рівні їх уявні частини: x1=x2,
y1=y2
. Зокрема, комплексне число
рівно нулю тоді і тільки тоді, коли
x=y=0
. Поняття «більше» і «менше» для
комплексних чисел не вводяться.
Два
комплексні числа
і
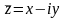 ,
відмінні лише знаком уявної частини,
називаються спряженими.
,
відмінні лише знаком уявної частини,
називаються спряженими.
7.3.2 Геометричне зображення комплексних чисел
В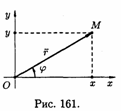 сяке
комплексне число
можна
зобразити точкою
сяке
комплексне число
можна
зобразити точкою
 площини Оху
такої, що х=Re
z,
y=Im
z.
І, навпаки, кожну точку
координатної площини можна розглядати
як образ комплексного числа
(див. рис. 161).
площини Оху
такої, що х=Re
z,
y=Im
z.
І, навпаки, кожну точку
координатної площини можна розглядати
як образ комплексного числа
(див. рис. 161).
Площина,
на якій зображаються комплексні числа,
називається комплексною
площиною.
Вісь абсцис називається дійсною
віссю,
оскільки
на ній лежать дійсні числа
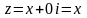 .
Вісь ординат називається уявною віссю,
на ній лежать чисто уявні комплексні
числа.
.
Вісь ординат називається уявною віссю,
на ній лежать чисто уявні комплексні
числа.
Комплексне
число
можна задавати за допомогою радіус-вектора
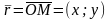 . Довжина вектора
. Довжина вектора
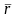 ,
що зображає комплексне число z
, називається модулем цього числа і
позначається
,
що зображає комплексне число z
, називається модулем цього числа і
позначається
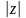 або r
. Величина кута між позитивним напрямом
дійсної осі і вектором
,
що зображає комплексне число, називається
аргументом цього комплексного числа,
позначається
Arg
z
або
або r
. Величина кута між позитивним напрямом
дійсної осі і вектором
,
що зображає комплексне число, називається
аргументом цього комплексного числа,
позначається
Arg
z
або
Аргумент
комплексного числа
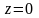 не визначений. Аргумент комплексного
числа
не визначений. Аргумент комплексного
числа
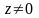 - величина багатозначна і визначається
з точністю до доданку 2πk
(k=0,
‑1, 1, -2, 2…):
Arg
z=arg
z+2
πk,
де arg
z
— головне значення аргументу, знаходиться
в проміжку (-π;
π],
тобто –
π<arg
z
≤
π
(іноді як головне значення аргументу
беруть величину, що належить проміжку
[0;2π)).
- величина багатозначна і визначається
з точністю до доданку 2πk
(k=0,
‑1, 1, -2, 2…):
Arg
z=arg
z+2
πk,
де arg
z
— головне значення аргументу, знаходиться
в проміжку (-π;
π],
тобто –
π<arg
z
≤
π
(іноді як головне значення аргументу
беруть величину, що належить проміжку
[0;2π)).
Ф орми запису комплексних чисел
Запис числа у вигляді z=x+iy називають алгебраїчною формою комплексного числа.
Модуль
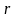 і аргумент φ
комплексного числа можна розглядати
як полярні координати вектора
і аргумент φ
комплексного числа можна розглядати
як полярні координати вектора
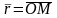 ,
що зображає комплексне число z=x+iy
(див.
рис. 162). Тоді одержуємо x=rcosφ,
y=rsinφ
. Отже, комплексне число можна записати
у вигляді z=
rcosφ+ir
sinφ
або
,
що зображає комплексне число z=x+iy
(див.
рис. 162). Тоді одержуємо x=rcosφ,
y=rsinφ
. Отже, комплексне число можна записати
у вигляді z=
rcosφ+ir
sinφ
або
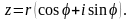
Такий запис комплексного числа називається тригонометричною формою.
Модуль
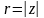 однозначно визначається по формулі
однозначно визначається по формулі

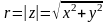
Наприклад,
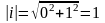 .
Аргумент φ
визначається з формул
.
Аргумент φ
визначається з формул
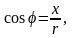
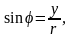

Оскільки

то
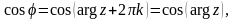
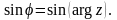
Тому
при переході від форми алгебри комплексного
числа до тригонометричної достатньо
визначити лише головне значення аргументу
комплексного числа
z,
тобто прочитати

Оскільки
π<arg
z
≤
π
, то з формули
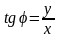
одержуємо, що
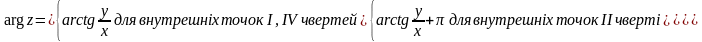
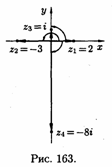
Якщо точка
лежить на дійсній або уявній осі, arg
z
то можна знайти безпосередньо (див. рис.
163). Наприклад, arg
z1=0
для z1=2
arg
z2=π
для z2=-3;
arg
z3=
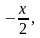 ; для і для
; для і для
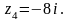
Використовуючи формулу Ейлера:
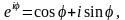
комплексне
число
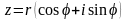 можна записати в так званій показниковій
(або експоненційній) формі z=r
можна записати в так званій показниковій
(або експоненційній) формі z=r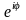 де
- модуль комплексного числа, а кут
де
- модуль комплексного числа, а кут
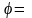 Arg
z=
arg
z+2kπ
(k=0,-1,1,-2,2…).
Arg
z=
arg
z+2kπ
(k=0,-1,1,-2,2…).
Через формулу Ейлера, функція періодична з основним періодом 2π . Для запису комплексного числа z в показовій формі, достатньо знайти головне значення аргументу комплексного числа, тобто прочитати φ=arg z .
Приклад
7.3.1
Записати
комплексні числа
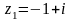 і x2=-1
в тригонометричній і показовій формах.
і x2=-1
в тригонометричній і показовій формах.
○ Для
 маємо
маємо
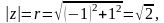
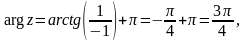 тобто
тобто

Тому
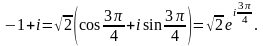
Для
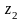 маємо
маємо
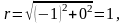
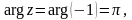
тобто Тому
Тому
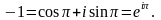 ●
●
