7.1.4. Максимум і мінімум функцій

Точка називається точкою максимуму функції, якщо існує такий окіл точки що для всіх з цієї околиці виконується нерівність .

Аналогічно визначається точка мінімуму функції: – точка мінімуму функції, якщо 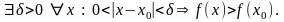На малюнку 146

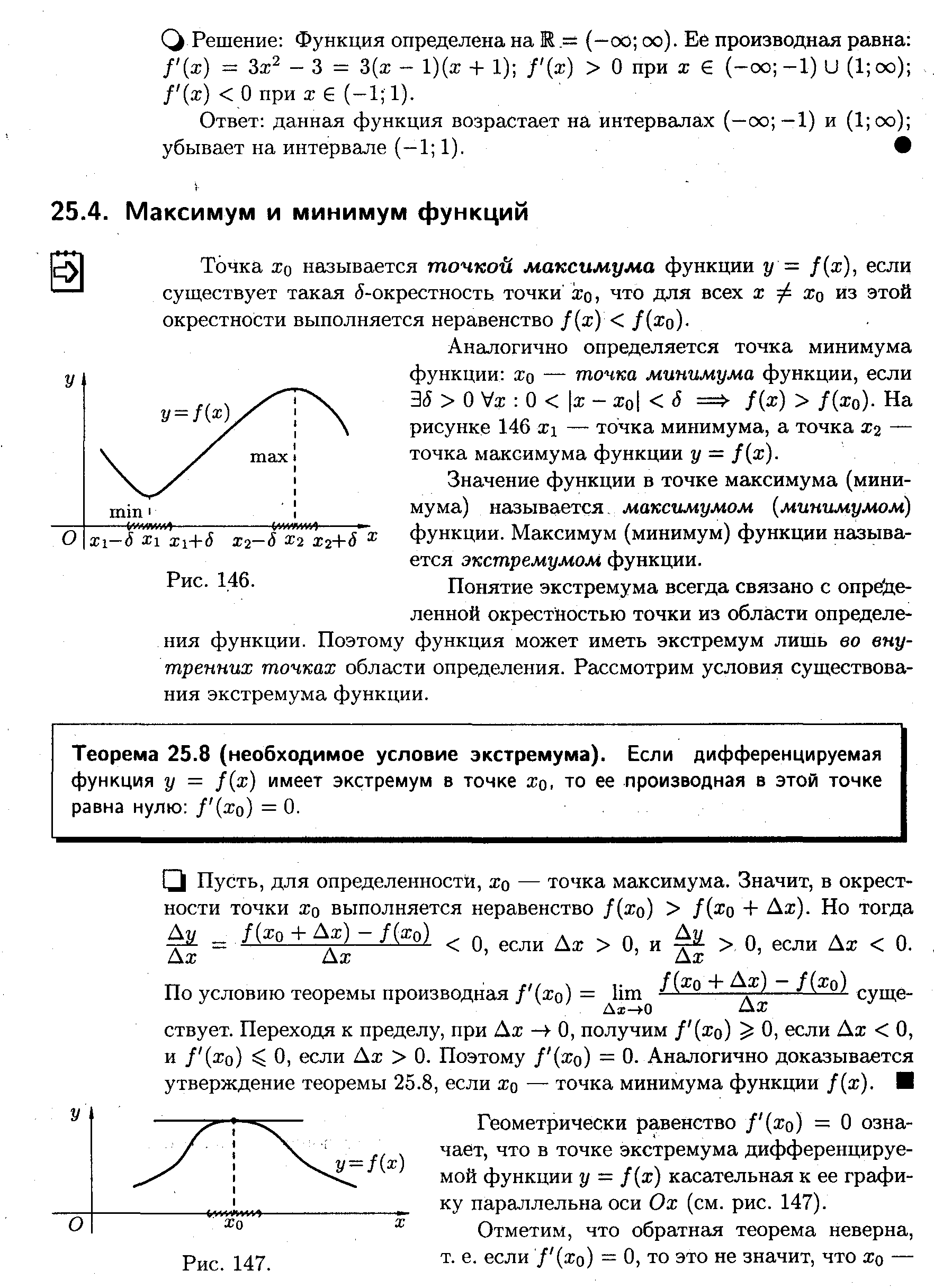х₁ – точка мінімуму, а точка х₂ – точка максимуму функції .

Значення функції в точці максимуму (мінімуму) називається максимумом (мінімумом) функції. Максимум (мінімум) називається екстремумом функції.

Рис. 146

Поняття екстремуму завжди пов'язано з певною околицею точки з області визначення функції. Тому функція може мати екстремум лише у внутрішніх точках області визначення. Розглянемо умови існування екстремуму функції.

Теорема 7.1.8 (необхідна умова екстремуму). Якщо функція , що диференціюється, має екстремум в точці , то її похідна в цій точці рівна нулю .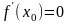

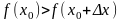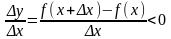□ Нехай, для визначеності, – точка максимуму. Значить, в околиці точки виконується нерівність . Але тоді , якщо, і , якщо 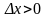. По умові теореми похідна існує. Переходячи до границі, при, отримаємо , якщо

Рис. 147.

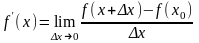
і 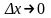, якщо . Тому . Аналогічно доводиться твердженя теореми 25.8, якщо – точка мінімуму функції .

Геометрично рівність означає, що в точці екстремуму функції , що диференціюється, дотична до її графіка

паралель до осі Ох (див. Рис. 147).

В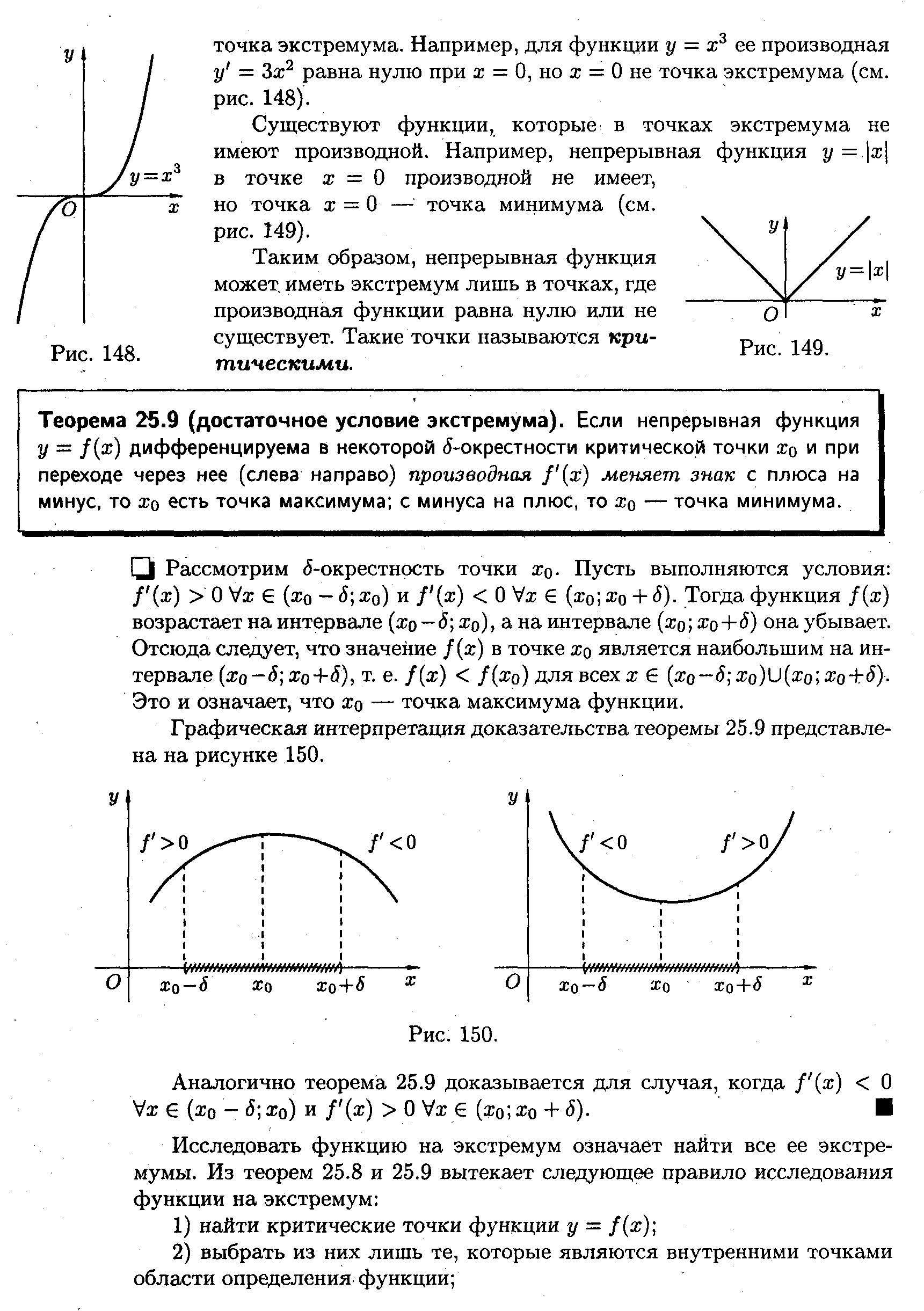 ідзначимо що зворотна теорема невірна, тобто якщо , то це не значить, що – точка екстремуму .

Наприклад, для функції її похідна рівна нулю при х, але х не точка екстремуму (див. Рис. 148).

Існують функції, які в точках екстремуму не мають похідній. Наприклад, неперервна функція 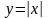в точці х

Рис. 149. похідної не має,

але точка х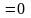 – точка мінімуму (див. Рис. 149).

Т аким чином, неперервна функція може має екстремум лише в точках, де похідна функції рівна нулю або не існує. Такі точки називаються критичними. ■

Рис. 148.

Теорема 7.1.9 (достатня умова екстремуму). Якщо неперервна функція диференціюється в деякому – околі критичної точки і під час переходу через неї (зліва направо) похідна міняє знак з плюса на мінус, то точка максимуму; з мінуса на плюс, то – точка мінімуму.

□Розглянемо – околиця точки . Нехай виконуються умови:

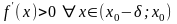і . Тоді функція зростає на інтервалі, а на інтервалі вона убуває. Звідси витікає, що значення в точці є найбільшим на інтервалі, тобто для всіх . Це означає, що – точка максимуму функції.

Графічна інтерпретація доведення теореми 7.1.9 представлена на малюнку 150.

Рис.150.

Аналогічно теоремі 25.9 доводиться для випадку, коли і .

Досліджувати функцію на екстремум означає знайти всі її екстремуми. З теорем 7.1.8, 7.1.9 витікає наступне правило дослідження функції на екстремум:

1. знайти критичні точки функції ;

вибрати з них лише ті, які є внутрішніми точками області визначення функції;

2. досліджувати знак похідної зліва і справа до кожної з вибраних критичних крапок;

3. відповідно до теореми 25.9 (достатня умова екстремуму ) виписати точки екстремуму (якщо вони є) і обчислити значення функції в них.■

Приклад 7.1.9. Знайти екстремум функції .

○ Очевидно . Знаходимо, тобто .●

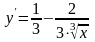Похідна не існує при і рівна нулю при. Ці точки розбивають всю область визначення даної функції на три інтервали . Відзначимо на малюнку 151 знаки похідної зліва і праворуч від кожної з критичних крапок.

Рис. 151.

Отже, – точка максимуму, і =8– точка мінімуму .

Іноді буває зручним викорислтовувати іншу достатню ознаку існування екстремуму, засновану на визначенні знака другої похідної.

Теорема 7.1.10. Якщо в точці перша похідна функції рівна нулю і (), а друга похідна в точці існує і відмінна від нуля (), то при в точці функція має максимум і мінімум– при .

□Нехай для визначеності 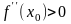. Оскільки

,

то в достатньо малій околиці точки . Якщо, то, якщо, то .

Таким чином, під час переходу через крапку першу похідну міняє знак з мінуса на плюс. Отже, по теоремі 7.1.9, є точка мінімуму.

Аналогічно доводиться, що якщо , то в точці 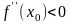функція має максимуму.■