4.4 Расчет несимметричных конфигураций

Для расчета напряжений и ком­пенсирующей способности несиммет­ричных конфигураций трубопрово­дов удобно пользоваться методом фиктивных нагрузок.

Если эпюру изгибающих момен­тов, действующих на трубопровод, принять за фиктивную нагрузку, то угол поворота любого сечения тру­бы равен перерезывающей силе фиктивной нагрузки, деленной на жесткость (EJ), а стрела прогиба равна моменту фиктивной нагрузки, деленной на жесткость.

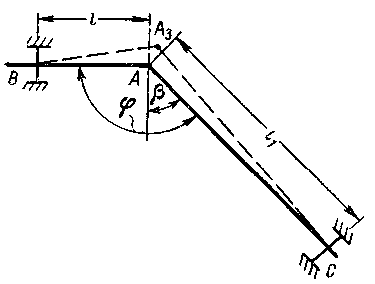
Рис. 9. Схема угловой компенсации.

Для расчета максимального из­гибающего напряжения, возникаю­щего в трубопроводе с угловой кон­фигурацией (рис. 9), используется формула:

, (20)

где Δ — удлинение короткого пле­ча, м; l — длина короткого плеча, м;

n— отношение длины длинного плеча к длине короткого (n = l₁/ l); β = φ — 90°.

При φ = 90° или β = 0

σ = 1,5 [ ΔЕd (n+l) / l²]. (21)

Максимальное напряжение воз­никает в коротком плече в месте защемления у мертвой опоры.

Расчет величины ожидаемого бокового смещения можно опреде­лить на основе тригонометрических соотношений.

Максимальное боковое смещение короткого плеча у колена

Δк = Δ (n + sin β) / cosβ. (22)

Максимальное боковое смещение длинного плеча у колена

Δд = Δ (1 + n sin β) / cos β. (23)

4.5. Пространственные трубопроводы

В пространственных трубопроводах, кроме деформаций, растяжений и изгиба, имеющих место в плоских трубопроводах, возникают деформации кручения.

На рис. 10 показана схема простран­ственного трубопровода. При нагревании трубопровода в плече АВ возникает дефор­мация кручения, вызываемая термическим удлинением плеча CD. Аналогичная дефор­мация кручения возникает и в плече CD, вызванная термическим удлинением пле­ча АВ.

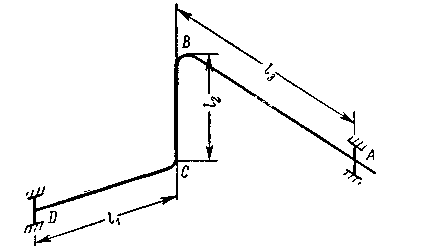
Рис. 10. Схема пространственного трубопровода.

Максимальное напряжение кручения возникает в концевых сечениях трубопроводов, на которые передаются крутящие мо­менты (сечения у отвода В и С) на наружной поверхности трубы и определяется по формуле

τ = Gί_к, (24)

где G — модуль сдвига; ί_к — относительное кручение,

ί_к = φr / l, (25)

где φ — угол поворота сечения трубопро­вода в радианах;

г — наружный радиус трубы;

l — длина плеча трубопровода.

Как видно из выражений (24) и (25), напряжение кручения не зависит от толщи­ны станки трубопровода.

Величина крутящего момента опреде­ляется по формуле

M_К = τW_К, (26)

где W_К—полярный момент сопротивления трубы, м3.