9

Тема: КОМПЕНСАЦИЯ ТЕМПЕРАТУРНЫХ ДЕФОРМАЦИЙ ТРУБОПРОВОДОВ

1. Общие положения

Компенсация температурных де­формаций стальных трубопроводов имеет исключительно важное зна­чение в технике транспорта тепла.

Если в трубопроводе отсутствует компенсация температурных дефор­маций, то при сильном нагревании в стенке трубопровода возникают большие напряжения, опасные для прочности.

Величина этих напряжений мо­жет быть определена по закону Гука

σ = Ei, (1)

где Е — модуль упругости; i — относительная деформация.

При повышении темпера­туры трубопровода длиной l удлинение должно составить:

Δl =αlΔt, (2)

где α — коэффициент линейного удлинения; Δt – изменение температуры стенки трубопровода, ⁰С.

Для углеродистой стали α = 12·10^-6 1/град. Если участок трубы защемлен и при нагревании не удлиняется, то его относительное сжатие равно:

i = Δl/l = αΔt. (3)

Из совместного решения уравнений (1) и (3) находится напряже­ние сжатия, возникающее при на­греве прямолинейного защемленно­го (без компенсаторов) участка трубопровода

σ = αEΔt. (4)

Как видно из формулы (4), напряжение сжатия, возникающее в защемленном прямолинейном участке трубопровода, не зависит от диаметра, толщины стенки и дли­ны трубопровода, а зависит толь­ко от материала (модуль упругости и коэффициент линейного удлине­ния) и перепада температур.

Усилие сжатия, возникающее при нагревании в прямолинейном трубопроводе без компенсации, определяется по формуле

P=σf = Eif, (5)

где f – площадь поперечного сечения стенки трубопровода, м².

Для уменьшения указанных напряжений применяются осевые и радиальные компенсаторы. Осевые компенсаторы служат для поглощения температурных удлинений прямолинейных участков трубопроводов.

Радиальные компенсаторы могут быть использованы при любой конфигурации трубопроводов.

2. Осевая компенсация

На практике находят примене­ние осевые компенсаторы двух ти­пов: скользящие (сальниковые и манжетные) и упругие.

На рис. 1 показан сальнико­вый компенсатор одностороннего типа сварной конструкции. В тепловых сетях могут применяться компенсаторы двустороннего типа.

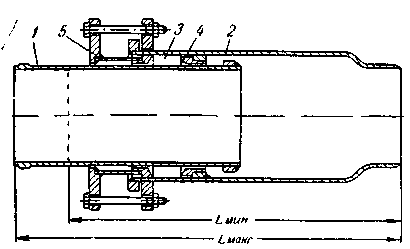
Рис. 1. Одинарный сальниковый ком­пенсатор сварной конструкции.

1 — стакан; 2 — корпус; 3 — сальниковое уплотне­ние; 4 — упорное кольцо; 5 — грундбукса.

Сальниковая набивка, обеспечивающая плотность, зажимается между упорным кольцом 4 и грундбуксой 5. Обычно на­бивка выполняется из асбестовых прографиченных колец квадратного» сечения. Компенсатор непосред­ственно вваривается в трубопровод, поэтому установка его на линии нe приводит к увеличению количества фланцевых соединений.

Для того чтобы предупредить возникновение растягивающих уси­лий в трубопроводе в случае пони­жения температуры его ниже тем­пературы монтажа, необходимо при установке компенсатора оставлять достаточный зазор между буртом стакана и упорным кольцом корпу­са компенсатора. Перед присоеди­нением сальникового компенсатора к трубопроводу необходимо тща­тельно выверить линию во избежа­ние перекосов и заеданий стакана в корпусе.

Недостатком сальниковых ком­пенсаторов всех типов являете» сальник, требующий систематиче­ского и тщательного ухода в экс­плуатации. Набивка в сальниковом компенсаторе изнашивается, теряет со временем упругость и начинает пропускать теплоноситель. Подтяж­ка сальника в этих случаях не дает положительных результатов, поэто­му через определенные периоды времени сальники приходится пере­бивать.

В манжетных компенсаторах уплотне­ние достигается за счет «прижима» гибкой манжеты, изготовленной из термостойкой резины, к поверхности стакана компенса­тора.

При увеличении давления рабочей сре­ды растет усилие, прижимающее манже­ту к стакану.

Основным недостатком всех скользящих компенсаторов являет­ся утечка теплоносителя при ухуд­шении состояния уплотнительного устройства (сальника или манже­ты) вследствие его износа или ста­рения.

От этого недостатка свободны все типы упругих компенсаторов.

В тепловых сетях иногда приме­няются линзовые компенсаторы, несмотря на относительно небольшую их компенсирующую способность и большую осевую ре­акцию, передаваемую на мертвые опоры.

На рис. 2 приведена конст­рукция трехволновото линзового компенсатора. Линзовые компенса­торы изготовляются из листовой стали. Для уменьшения гидравли­ческого сопротивления линзовых компенсаторов внутрь корпуса вставляется гладкая труба.

Линзовые компенсаторы сварно­го типа находят основное примене­ние на трубопроводах низкого дав­ления (до 0.4 – 0,5 Мпа). При установ­ке на трубопроводах более высоко­го давления возможно выпучивание волн. Для придания большей жест­кости против выпучивания прихо­дится делать линзы из листов боль­шой толщины, что ведет к

пониже­нию их компенсирующей способно­сти. Для поглощения больших термических деформаций линзовые компенсаторы выполняются с боль­шим количеством волн.

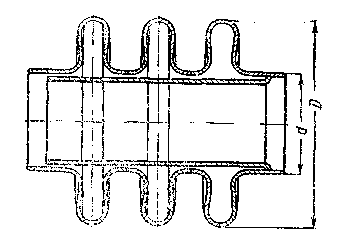
Рис. 2. Трёхволновой линзовый компенсатор,

Осевая реакция линзовых ком­пенсаторов состоит из двух слагае­мых:

S= S_к + S_д, (6)

где S_к — осевая реакция от темпе­ратурной компенсации, вы­зываемая деформацией волны при термическом расширении трубопрово­да, кН; S_д — осевая реакция, вызывае­мая внутренним давле­нием, кН.

Осевая реакция от температур­ной компенсации может быть опре­делена по формуле

S_к = (Δ / n ) ε, (7)

где Δ — тепловая деформация ком­пенсатора, м, n — число волн; ε— жесткость волны,

кН / м.

Жесткость волны ε зависит от профиля волны, её геометрических размеров и толщины стенки компенсатора и равна осевому усилию, необходимому для сжатия волны на 1 м, Величина определяется экспериментально.

Осевая реакция внутреннего давления может быть определена по формуле

S_д = φ ( D² – d² ) p_и, (8)

где D, d — наружный и внутренний диаметры волны, м; р_и— избыточное давление теплоносителя, кПа; φ — опытный коэффициент, зависящий от геометри­ческих размеров и тол­щины стенки волны.

В большинстве случаев φ ≈ 0,5—0,6.

3. Радиальная компенсация

При радиальной компенсации термическая деформация трубопро­вода воспринимается за счет изги­ба специальных эластичных вставок или отдельных участков самого трубопровода.

Последний метод компенсации тепловых деформаций называется естественной компенсацией. Естест­венная компенсация находит широ­кое применение на практике.

Преи­муществами ее над другими вида­ми компенсации являются: просто­та устройства, надежность, отсутствие необходимости в надзоре и ухо­де, разгруженность мертвых опор от усилий внутреннего давления.

Недостатком естественной ком­пенсации является поперечное перемещение деформи- руемых участ­ков трубопровода, требующее уве­личения ширины непроходных ка­налов и затрудняющее применение засыпных изоляций и бесканаль­ных конструкций.

При сооружении теплопроводов следует максимально использовать все естественные повороты и изги­бы трубопроводов для компенсации тепловых удлинений. К применению специальных компенсаторов реко­мендуется прибегать лишь после использования всех возможностей естественной компенсации.

Расчет естественной компенса­ции заключается в нахождении уси­лий и напряжений, возникающих в трубопроводе под действием упругой деформации. Методика расчета базируется на основных за­конах теории упругости, связываю­щих величины деформации с дей­ствующими усилиями.

Участки трубопровода, воспри­нимающие температурные деформа­ции при естественной компенсации, состоят из колен и прямых участков. Гнутые колена повышают гиб­кость трубопровода и увеличивают его компенсирующую способность. Влияние гнутых колен на компенси­рующую способность особенно за­метно в трубопроводах большого диаметра.

Изгиб кривых участков труб со­провождается сплющиванием попе­речного сечения, которое превра­щается из круглого в эллиптиче­ское.

На рис. 3 показана изогнутая труба с радиусом кривизны R. Вы­делим двумя сечениями ab и cd эле­мент трубы. При изгибе в стенке трубы с выпуклой стороны возни­кают растягивающие, а с вогну­той— сжимающие усилия. Как рас­тягивающие, так и сжимающие уси­лия дают равнодействующие Т, нормальные к нейтральной оси.

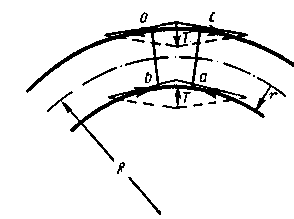
Рис. 3. Сплющивание кри­вой трубы при изгибе.

Под действием сил Т поперечное сечение трубы сплющивается и превращается из круглого в эллиптическое. При сплющивании жест­кость трубы понижается. Коэф­фициент понижения жест­кости трубы вследствие сплю­щивания определяется следующей формулой:

k= ( 1+12 h²) / (10 + 12h² ), {9)

где h — так называемый коэффи­циент трубы, который на­ходится по формуле

h = δR / r², (10)

где δ — толщина стенки трубы ; R —радиус изгиба оси трубы; г —средний радиус поперечно­го сечения трубы.

Формула (9) действительна при значениях коэффициента трубы h >0,3. Значения k приведены на рис. 4.

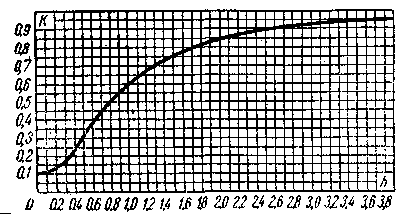
Рис. 4. Зависимость коэффициента понижения жестко­сти гнутых труб от коэффициента трубы.

Для прямой трубы коэффициент понижения жесткости трубы k = 1.

С увеличением диаметра трубы значение коэффициента понижения жесткости k падает.

Одновременно с переходом круг­лого сечения трубы в эллиптиче­ское вследствие сплющивания про­исходит изменение напряжения от изгиба и перераспределение этого напряжения по сечению трубы. Ес­ли максимальное напряжение, воз­никающее при изгибе круглой тру­бы, обозначить через σ, то макси­мальное напряжение, возникающее в трубе со сплющенным сечением, при той же величине деформации составит mσ, где m — поправочный коэффициент на­пряжения для гнутых гладких труб.

Поправочный коэффициент на­пряжения m для гнутых труб по сравнению с прямыми трубами при 0,2< h <2 определяется следую­щей зависимостью:

m = 2 /3k . (11)

Значение поправочного коэффи­циента m приведено на рис. 5.

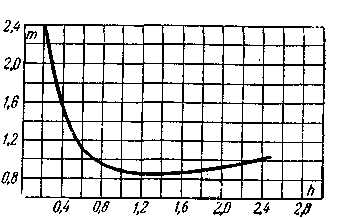
Рис. 5. Зависимость коррекционного коэффициента напряжения от коэффициента трубы.

При малых значениях коэффи­циента трубы h, т. е. для труб большого диаметра, поправочный коэффициент m достаточно высок, значительно превышает единицу. По мере уменьшения диаметра тру­бопровода и связанного с этим ро­ста коэффициента трубы h значение поправочного коэффициента m па­дает. При коэффициенте трубы h≥0,6 поправочный коэффициент напряжения достигает величины, близкой к единице.

Для определения напряжений и компенсирующей способности сим­метричных конфигураций трубопро­водов, в которых прямая, соединя­ющая смежные мертвые опоры, совпадает с осью трубо­провода, удобно поль­зоваться методом, ос­нованным на теории изгиба кривого бруса.

4. Расчет компенсаторов