МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВПО Алтайский государственный технический университет

им. И. И. Ползунова

Кафедра «Прикладная механика»

Курсовая работа

защищена с оценкой___________

«___»_______________20___г.

Курсовая работа

по дисциплине «Вычислительная математика»

на тему: Численное интегрирование разными методами

Вариант 13

Выполнил студент

Гр. Ин-01: _______ Тюняева Ю. А.

Преподаватель: _______ Перфильева А. Д.

Барнаул, 2012

Содержание:

Задание…………………………………………………………………………….3

Исходные данные…………………………………………………………………4

1. ВЫЧИСЛЕНИЕ ИНТЕРГРАЛА 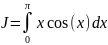аналитически, методом средних прямоугольников, методом трапеций, методом Симпсона…………..5

1.1Аналитически……………………………………………………………….5

1.2 Метод средних прямоугольников………………………………………...5

1.2.1 Метод средних прямоугольников при n=1………………………...6

1.2.2 Метод средних прямоугольников при n=2………………………...6

1.3 Метод трапеций……………………………………………………………7

1.3.1 Метод трапеций при n=1……………………………………………7

1.3.2 Метод трапеций при n=2…………………………………………….8

1.4 Метод Симпсона…………………………………………………………...9

1.4.1 Метод Симпсона при n =1…………………………………………...9

2. Метод Симпсона при n=2…………………………………………...9

2. Вычисление интеграла методом Гаусса……………...10

2.1 Одноточечная схема метода Гаусса…………………………………….11

2.2 Двухточечная схема метода Гаусса…………………………………….11

3. Трехточечная схема метода Гаусса……………………………………..12

3. Сравнительный анализ точности полученных результатов………………..13

4. Вычисление интеграла 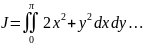………………………….14

1. Аналитически……………………………………………………………..14

2. Метод Гаусса……………………………………………………………...14

4.2.1Одноточечная схема……………………………………………..14

4.2.2 Двухточечная схема……………………………………………14

Вывод……………………………………………………………………………..16

Задание:

1. Вычислить интеграл 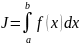аналитически, а затем численно методами средних прямоугольников, трапеций, Симпсона, принимая n=1 и n=2 (n-количество разбиений отрезка интегрирования).

2. Вычислить этот же интеграл методом Гаусса по одноточечной, двух точечной и трехточечной схемам интегрирования.

3. Сделать сравнительный анализ точности полученных результатов.

4. Вычислить интеграл 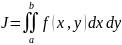аналитически, а затем численно методом Гаусса по одноточечной и двухточечной схемам. Сравнить результаты.

Исходные данные:

a = 0

b =

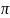
f(x) = x cos(x)

f(x,y) = 2x² + y²

1.Вычисление интерграла аналитически, методом средних прямоугольников, методом трапеций, методом Симпсона.

1. Аналитически.

Для вычисления данного интеграла используем формулу интегрирования по частям: .

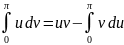Пусть:

u = x

dv = cos (x) dx

Тогда:

du = dx

v = sin(x)

Следовательно:

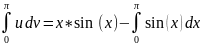
Откуда получаем:

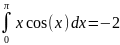
1.2 Метод средних прямоугольников

Метод прямоугольников получается при замене подынтегральной функции на константу. В качестве константы можно взять значение функции в любой точке отрезка  . Наиболее часто используются значения функции в середине отрезка и на его концах. Соответствующие модификации носят названия методов средних прямоугольников, левых прямоугольников и правых прямоугольников.

По методу средних прямоугольников на интервале [x_i,x_i+h]имеем

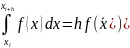
1.2.1 Метод средних прямоугольников для n=1.

При n=1:

x_i=a

x_i+h=b

=

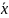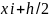
h=(b-a)/n

Исходя из этого получаем уравнение:

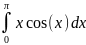= ((b-a)/n) * ( cos( ))

Подставляя в полученное уравнение исходные данные получаем:

=(( - 0)/1)*((0+(( - 0)/1)/2)*cos(0+(( - 0)/1)/2)) = 0

= 0

Погрешность:

R=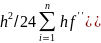 =-2,584

1.2.2 Метод средних прямоугольников для n=2

В данном случае исходный отрезок интегрирования разбивается на 2 отрезка интегрирования: (0;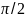 ) и ( ; ).

В связи с этим:

X₁=0

X₂=

=

h=(b-a)/n

По полученным данным получаем уравнение:

= ((b-a)/2)*(((x₁+(b-a)/4)*(cos(x₁+(b-a)/4))+((x₂+(b-a)/4)* *(cos(x₂+(b-a)/4))

Подставляем в полученное уравнение начальные данные и получаем:

= (( -0)/2)*(((0+( -0)/4)*(cos(0+( -0)/4))+( ( +( -0)/4)* *(cos( + ( -0)/4)) = -1,745

= -1,745

Погрешность:

R= =-0,636