6. Применение парно-доминантного метода для принятия оптимального управленческого решения.

Пусть х–решение, возможные варианты которого определены на допустимом множестве Х. Качество решения оценивается n скалярными критериями R_j, j=1, 2, …, n, оценки по которым образуют вектор эффективности r–(r₁, …, r_n). Этот вектор связан с альтернативой х функциональным отображением F: XR, которое может быть задано аналитически, статистически или эвристически. Необходимо найти подмножество лучших вариантовY_x, удовлетворяющий требованиям следующего вида:

_,

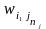Приведенная постановка задачи соответствует критериально – экстремизационному выбору. При постановке критериально – экстремизационной задачи предполагается, что критериальная оценка r(x) варианта х зависит только от этого варианта и совершенно не зависит от того, какие другие варианты включены в множество Х. В частности, если рассматривать не фиксированное Х, а различные его подмножества АХ, содержащие вариант хА, то при критериально – экстремизационном подходе оценки r(x) не изменяются для всех х на всех А.

Множество вариантов Y_x называется множеством Парето для Х. Это множество обладает тем свойством, что все принадлежащие ему альтернативы не могут быть улучшены одновременно по всем критериям. Способам его выделения в конкретных задачах, оценке его мощности и способам его усечения посвящено множество работ.

Проблема выделения множества Парето в общем виде не решена. Хорошо разработаны методы отыскания эффективных точек для задач с двумя критериями и для линейных задач. Большинство известных алгоритмов достаточно трудоемки, а получаемые на их основе множества представляют собой области сложной структуры в пространстве 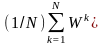, как правило, невыпуклые и несвязные. Когда область Парето содержит множество элементов, то для полного упорядочения векторных оценок необходима дополнительная информация. В качестве такой информации обычно используются предпочтения лица, принимающего решения (ЛПР).

Понятия «критерий» и «максимум» могут быть обобщены на случай применения порядковой шкалы для измерения качества альтернатив. Если варианты x и y сравниваются попарно, то отношения между ними можно представить в виде бинарного отношения xDy. Тогда правило выделения лучших вариантов можно записать в виде:

_,

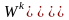Выделенные с помощью этого правила варианты называются не запрещенными по отношению D вариантами в множестве Х. Исследованию бинарных отношений с позиций теории выбора посвящены работы [4, 37, 92, 109, 166]. При переходе от критериальных оценок альтернатив к произвольным парным сравнениям сохраняется свойство независимости от контекста. Учитывая это свойство, такой выбор называется парнодоминантным или графодоминантным выбором.

Парнодоминантный выбор может быть сведен к критериально – экстремизационному в случае, если бинарное отношение D является ациклическим и транзитивным. Если при этом отношение D является антирефлексивным, то выбор будет оптимальным по Парето.

Почти до начала 80-х годов 20 века считалось, что почти всякий разумный выбор сводится к парнодоминантному. Ситуации, в которых это оказывалось невозможным, рассматривались как исключения. В настоящее время представления о рациональном выборе изменились, и транзитивность отношения D перестала считаться необходимой.