23. Применение критерия минимального сожаления (Севиджа) для принятия оптимального управленческого решения

Критерий решения Сэйвиджа, иногда называемый критерием потери от мини-макса, исследует убытки, которые представляют собой понесенные по-тери в результате принятия неправильного решения. Потеря измеряется как абсолютная разность между отдачей для данной стратегии и отдачей для наиболее эффективной стратегии в пределах одного и того же состояния эко-номики.

Суть измерения потерь совершенно проста. Если любое конкретное со-стояние экономики возникает в будущем и если мы выбрали стратегию, кото-рая обеспечивает максимальную отдачу для этого состояния, то мы не считаем потери. Но если мы выбрали любую другую стратегию, то потеря представляет собой разность между тем, что происходит фактически, и тем, что мы получили бы, приняв более оптимальное решение.

Минимаксный критерий Сэвиджа. В соответствии с этим критерием, если требуется в любых условиях избежать большого риска, то оптимальным будет то решение, для которого риск, максимальный при различных вариантах усло-вий, окажется минимальным.

Критерий минимаксного риска Сэвиджа. При его использовании обеспе-чивается наименьшее значение максимальной величины риска:

S = min_i max_j r_i,j

где риск rij определяется выражением: ri,j = βj – αi,j; βj – максимально возможный выигрыш.

Критерий Сэвиджа, как и критерий Вальда, – это критерий крайнего пессимизма, но только пессимизм здесь проявляется в том, что минимизируется максимальная потеря в выигрыше, по сравнению с тем, чего можно было бы достичь в данных условиях.

24. Применение критерия оптимизма-пессимизма (л.Гурвица) для принятия оптимального управленческого решения

Критерий устойчивости Рауса-Гурвица — один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицом. Наряду с критерием Рауса является представителем семейства алгебраических критериев устойчивости, в отличие от частотных критериев, таких как критерий устойчивости Найквиста. Достоинством метода является принципиальная простота, недостатком - необходимость выполнения операции вычисления определителя, которая связана с определенными вычислительными тонкостями. Критерий пессимизма-оптимизма Гурвица рекомендует при выборе решения не руководствоваться ни крайним пессимизмом ни крайним оптимизмом.

3) Критерий пессимизма-оптимизма Гурвица. Здесь представляется логичным, чтобы при выборе решения вместо двух крайностей в оценке ситуации (оптимизм-пессимизм) придерживаться некоторого компромисса, учитывающего возможность как наихудшего, так и наилучшего поведения «природы». В соответствии с этим компромиссным критерием для каждого решения будет линейная комбинация минимального и максимального выигрышей и выбирается тот, для которого эта величина окажется наибольшей:

где х — показатель пессимизма-оптимизма (чаще всего 0,5).

Критерий пессимизма-оптимизма Гурвица:

G = max [xB™in +(!-*) В™ах ], где х — доля оптимизма-пессимизма (0,5).

В-третьих, может иметь место требование выбрать решение между линией поведения в расчете на худшее и линией поведения в расчете на лучшее. В этом случае оптимальным решением будет то, для которого окажется максимальным показатель G (так называемый критерий пессимизма-оптимизма Гурвица),

25 Принципы де Кондорсе и Борда для принятия коллективных решений

Принцип Кондорсе

Кондорсе определил правило, по которому сравнение выбираемых альтернатив (кандидатов) производится с учетом полной ординалисткой информации о предпочтениях избирателей.

Согласно принципу Кондорсе, для определения истинной воли большинства необходимо, чтобы каждый голосующий проранжировал всех кандидатов в порядке их предпочтения. После этого для каждой пары кандидатов определяется, сколько голосующих предпочитает одного кандидата другому - формируется полная матрица попарных предпочтений избирателей.

На базе этой матрицы, используя транзитивность отношения предпочтения, можно попытаться построить коллективную ранжировку кандидатов.

Пример применения принципа

Приведём численный пример из работы Кондорсе.

Введём для краткости обозначение: будет означать, что голосующий предпочитает кандидата A кандидату B, а кандидата B — кандидату С.

П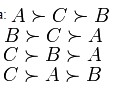 усть 60 голосующих дали следующие предпочтения:

23 человека:

19 человек:

16 человек:

2 человека:

При сравнении A с B имеем: 23 + 2 = 25 человек за то, что , и 19 + 16 = 35 человек за то, что .

По принципу Кондорсе мнение большинства состоит в том, что В лучше А.

Сравнивая А и С, будем иметь: 23 человека за и 37 человек за . Отсюда, по Кондорсе, заключаем, что большинство предпочитает кандидата С кандидату А. Аналогично (19 человек за , 41 человек за ) С более предпочтителен, чем B.

Таким образом, по Кондорсе воля большинства выражается в виде трех суждений: ; ; , которые можно объединить в одно отношение предпочтения C > B > A и если необходимо выбрать одного из кандидатов, то, согласно принципу Кондорсе, следует предпочесть кандидата С.