Экзаменационный билет № 27

1) а) + А + АВ б)

2) Сумма кратна пяти – 5 и 10. Считаем количество комбинаций: 1-4, 2-3, 3-2, 4-1, 4-6, 5-5, 6-4. Всего 7. Вероятность равна 7/36

3) + + = 0.1*0.2*0.7 + 0.9*0.2*0.3 + 0.1*0.8*0.3 = 0.092

4) Формула Байеса. Вероятность достать брак: 0.4*0.02+0.35*0.03+0.25*0.05 = 0.031. Вероятность того, что этот брак первого автомата: 0.4*0.02/0.031 = 0.258

5) p = 0.9, q = 0.1, n = 3; MX = 2.7; DX = 0.27

P(0) = 0.001 P(1) = *0.9*0.01 = 0.027 P(2) = 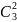*0.81*0.1 = 0.243 P(3) = 0.9³ = 0.729

6) Функция Лапласа (интегральная теорема Муавра-Лапласа 0_о). P(|X-MX|<1.5) = Ф(1.5/4.6) = 0.2586

7) Неравенство Маркова. P(X<60) > 1 – 15/60; P > 0.75

8) Всего комбинаций 5!, искомых: 2*2*1*1*1 = 4. Вероятность равна 1/30.

Экзаменационный билет № 19

1) а) + А + б) АВ + А С + ВС

2) Достать первой Т – вероятность 1/5. Достать второй О – вероятность 2/4. Достать третьей Р – вероятность 2/3. Перемножаем, получаем вероятность 4/60 = 1/15.

3) АВ + А С + ВС = 0.8*0.7*0.1+0.8*0.3*0.9+0.2*0.7*0.9 = 0.398

4) Формула Байеса: 0.45*0.03/0.2*0.01+0.35*0.02+0.45*0.03 = 0.6

5) МХ = 2*5/12 = 5/6 Р(0) = = 7/22 Р(1) = = 35/66 Р(2) = 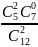= 5/33

6) Интегральная теорема Муавра-Лапласа. P(160<x<168) = 0.5(Ф((168-165)/4.6) – Ф((160-165)/4.6)) = 0.5*( 0.48431+ 0.72429) = 0.6043

7) MX = 2000*0.75 = 1500. Дана подсказка, что можно решить с помощью неравенства Чебышева. Отклонение от мат. ожидания находится как |1500-1550| = |1500-1450| = 50. DX = 1500*0.25 = 375. P(|X-MX| < 50) > 1 – 375/2500; P > 0.85

8) Объясняю подробно. Берем первого шахматиста. Он играет с остальными 13. Это 13 партий. Второй играет с 12 (с первым он уже сыграл). Третий – с 11 (сыграл с первыми двумя), четвертый – с 10, пятый – с 9, шестой – с 8, седьмой – с 7, восьмой – с 6, девятый – с 5, десятый – с 4, одиннадцатый – с 3, двенадцатый – с 2, и тринадцатый играет 1 партию с четырнадцатым, который, таким образом, отыграл все партии. Итого 13+12+11+10+9+8+7+6+5+4+3+2+1 = 91 партия.

Экзаменационный билет №20

1) а) + + б)

2) На первом месте номера без повторов может стоять любая из 10 цифр. На втором, т.к. повторов быть не должно – любая из оставшихся 9. На третьем – любая из 8 оставшихся, на четвертом – любая из 7 оставшихся, на пятом - любая из 6. Всего у нас 99999 вариантов (потому что начинаем мы с 00001). Вероятность равна 10*9*8*7*6/99999 = 0.3

3) = 1 - = 1 – 0.25*0.2*0.15 = 0.9925

4) Формула Байеса. Каждый стрелок делает по 1 выстрелу, всего выстрелов по мишени два. Т.е. 0.5 всего объема «работы» (по аналогии с задачами о бракованных изделиях) приходится на каждого стрелка. У первого вероятность выполнить «работу» 0.8, у второго 0.4. Далее – как и раньше: 0.8*0.5/(0.8*0.5+0.4*0.5) = 2/3

5) МХ = 2*4/7 = 8/7 Р(0) = = 1/7 Р(1) = 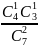= 4/7 Р(2) = 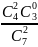= 2/7

6) Интегральная теорема Муавра-Лапласа: P(X<165) = 0.5(1 + Ф((165-165)/4.6)) = 0.5

7) Неравенство Маркова: P(X<80) > 1 – 16/80; P > 0.8

8) 7!*2. Как сказал дядя Толя, можно представить две книги, стоящие рядом, как одну, тогда получаем 7 объектов, находим количество перестановок через n!. Двойка же взялась там потому, что книги у нас различные. Следовательно, их тоже можно поменять местами между собой, 2!. Итого получаем 10080 вариантов.