Вариант 8

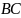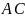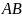1) а) + + б) + +

2) Количество вариантов для красной полосы на 1, 2 и 3 месте одинаково и равно 3*2 = 6. Итого 6*3 = 18 вариантов.

3) Количество искомых комбинаций: 1-3, 2-6, 3-1, 6-2 (4 штуки). Вероятность равна 1/9.

4) Вероятность равна 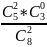= 5/14

5) Формула Байеса. (0.3*0.02)/(0.3*0.02+0.4*0.03+0.3*0.08) = 1/7

6) Р(0) = 0.4² = 0.16 Р(1) = *0.4*0.6 = 0.48 Р(2) = 0.6² = 0.36 МХ = 2*0.6 = 1.2

7) Вероятность того, что какая-либо секунда будет во время взгляда на часы равна 1/(60-0) = 1/60. Вероятность того, что время будет от 0 до 15 секунд равна (15-0)/(60-0) = 1/4.

8) Вероятность > 0.85. Нужно найти ξ из неравенства Маркова. 1 – 45/ξ = 0.85. 45/ξ = 0.15. ξ = 300. Итого получаем, что с вероятностью, большей 0.85, можно ожидать ветер со скоростью, не превышающей 300 км/ч.

Вариант 11

1) а) АВС б) + + + 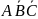или 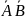+ + 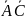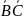(если есть какой-либо хороший вариант – напишите в ЛС)

2) 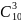* *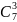 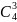= 16800

3) 16 искомых вариантов. Вероятность 4/9.

4) Аналогичная задача была подробно разобрана ранее в варианте 12, задача 4. Здесь приведу только полностью аналогичные вычисления.

2/7 * 5/6 * 4/5 * 1/4 = 1/21

5/7 * 2/6 * 4/5 * 1/4 = 1/21

5/7 * 4/6 * 2/5 * 1/4 = 1/21

В сумме получаем 1/7.

5) Формула Байеса. (0.15*0.6)/(0.15*0.6+0.7*0.3+0.15*0.1) = 2/7

6) Черных у нас 3. Остальные цвета нас не интересуют. Считаем вероятности.

Р(0) = 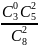= 5/14 Р(1) = 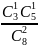= 15/28 Р(2) = 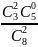= 3/28

7) В варианте 12, задаче 7 разобран подобный пример.

0.99 = 0.5(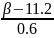Ф( ) - Ф( ))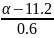

1.98 = Ф( ) - Ф( )

Ф( ) Є [0.98;1]; Ф( ) Є [-1; -0.98]

Є [2.33; 4]; Є [-4; -2.33]

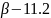Є [1.398; 2.4]; 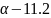Є [-2.4; -1.398]

Є [12.598; 13.4]; Є [8.8; 9.802]

Границы лежат от 8.8; 12.598 до 9.802; 13.4 (мог ошибиться в расчетах)

8) Опять непонятки по поводу того, что от нас хотят. Как и там, оценим сверху и снизу данную точку.

Р(Х>120) < 75/120; P < 5/8

P(X<120) > 1 – 75/120; P > 3/8

Вариант 15

1) а) + 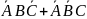б) АВ+ВС+АС

2) 32*32*10*10*10*10 = 10240000

3) 20 искомых вариантов, вероятность равна 5/9.

4) Общее количество комбинаций у нас 3⁸, количество искомых комбинаций - 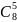* 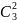. Вероятность по классической формуле равна ( * )/3⁸ = 0.0256

5) Знаменатель формулы Байеса, если вкратце. Нам нужно сложить вероятность того, что сделка принесет прибыль при уходе директора и при его отказе от ухода. Для этого перемножим соответствующие вероятности и сложим: 0.65*0.7+0.3*0.3 = 0.545

6) Что за ололо задача? 0_о МХ = np = 10*0.1 = 1. DX = npq = 10*0.1*0.9 = 0.9

7) MX = 160*0.95 = 152. Считаем по неравенству Маркова: P(X<155) > 1 – 152/155; P > 0.02. Странное значение получается. То ли опять закипаю, то ли такие числа в задачке.

8) Найдем DX как σ² = 4. Применим неравенство Чебышева: P(|X-MX|>5) < DX/5²; P < 0.16

Вариант 19

1) а) + +АВ б)

2) 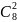* *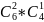 = 5040

3) Таких комбинаций 6. Вероятность 1/6.

4) Общее количество комбинаций – 3⁹. Количество нужных нам комбинаций - 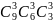. По формуле классической вероятности найдем вероятность: /3⁹ = 0.085

5) Находим вероятность перекладывания 2 белых, 2 черных и по шару каждого цвета через формулу, названия которой я упорно не могу вспомнить^{: .}

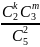Вероятность переложить 2 черных шара: 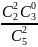⁼ 0.1

Вероятность переложить 2 белых шара: 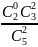⁼ 0.3

Вероятность переложить по шару каждого цвета: 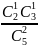= 0.6

Теперь находим для каждого варианта отдельную вероятность извлечь из второй урны после перекладывания белый шар. Всего шаров 8, изначально было по 4 каждого цвета. В первом случае добавляется 2 черных, становится 10 шаров, из них 4 белых. Вероятность равна 0.4. Во втором случае перекладывается 2 белых. Белых становится 6, вероятность 0.6. В третьем случае белых 5, вероятность 0.5. Теперь попарно перемножаем и складываем вероятности, чтобы найти вероятность извлечения из второй урны после перекладывания белый шар:

0.1*0.4+0.3*0.6+0.6*0.5 = 0.52

6) P(0) = 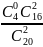= 12/19 P(1) = 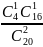= 32/95 P(2) = 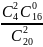= 3/95

7) МХ = 20*0.7 = 14. Неравенство Маркова: P(X>15) < 14/15.

8) DX < 5; имеются непонятные слова и маленькое отклонение, потому добавляем в знаменатель неравенства Чебышева еще и n = 2500, DX берем максимальную – 5:

P(|X-MX|< ε) > 1 – DX/nε²; P(|X-MX| < 0.4) > 1 – 5/2500*0.4²; P > 0.9875