Вариант 9

1) а) 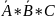+ + б) АВ + ВС + АС

2) 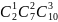= 5040

3) Меньше трех – это 1 или 2 очка на какой-либо из костей. 20 вариантов. Итого получаем вероятность 20*(1/36) = 5/9

4) Классическая вероятность – 3*(1/20)

5) Аналогичная задача уже была где-то. Вероятность того, что мы достанем бракованную деталь из первой партии – 1/12, вероятность достать небрак – 11/12. В первом случае (переложили бракованную) мы имеем вероятность извлечения из второй партии бракованной детали 2/11 (у нас стало всего 11 деталей в партии, из них две бракованные). Итоговая вероятность для первого случая – (1/12)*(2/11) = 1/66 = 2/132. Во втором случае (переложили небрак) вероятность извлечь бракованную деталь из второй партии равна 1/11. Итоговая вероятность для второго случая – (11/12)*(1/11) = 1/12 = 11/132. Суммарная вероятность извлечения после перекладывания детали из первой партии во вторую равна (2/132)+(11/132) = 13/132

6) Биномиальный закон распределения. МХ = np = 2*0.97 = 1.94.

P(0) = 0.03² = 0.0009

P(1) = 2 * 0.97 * 0.03 = 0.0582

P(2) = 0.97² = 0.9409

7) Нормальный закон распределения в упрощенной форме, когда у нас границы отрезка, в который попадают подходящие величины, равно отдалены от мат. ожидания. Для этого закона формула вероятности будет такова: P(|X-MX|<10) = Ф( ) = Ф(2) = 0.9545

8) Найдем размер отклонения, чтобы использовать неравенство Чебышева: 75000*0.02 = 1500. Найдем DX = npq = 75000*0.4*0.6 = 18000. P(|X-MX| < 1500) > 1 – (18000/1500²); P > 0.992

Вариант 17

1) а) б) АВ+ВС+АС

2) У нас есть три варианта рассадок тех пассажиров, которым пофиг, где сидеть, в отношении диванов. Т.е. первый, второй – спиной, третий – лицом, первый, третий спиной, второй лицом, второй, третий спиной, первый – лицом. Количество рассадок на каждом диване – 5! (сидящие там могут меняться, как хотят). Итого, чтобы найти общее количество рассадок, нужно посчитать произведение 3*5!*5! = 43200.

3) Таких вариантов 16. Вероятность равна 16*(1/36) = 4/9

4) Вероятность равна 1/343 = (1/7)³.

5) Первый автомат производит 2/3 деталей, второй – 1/3. Формула Байеса: = 28/45

6) МХ = 2*(3/10) = 0.6

Р(0) = =7/15 р(1) = = 7/15 р(2) = = 1/15

7) МХ = а = 5000*0.4 = 2000. DX = 5000*0.4*0.6 = 1200. σ = = 34.6. Используем функцию Лапласа: 0.99 = 0.5(Ф( ) – Ф(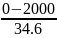 )); 1.98 = Ф( ) + 1; Ф( ) = 0.98; = 2.33; 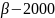= 80.6; = 2080.6

8) Неравенство Маркова. Р(Х>400) < 180/400; P < 0.45.

Вариант 13

1) а) A + В + С б)

2) Не менее двух – это 2, 3, 4 женщины. Проще сделать так: посчитать общее количество вариантов ( ), и отнять от него варианты с 0 и 1 женщинами. Выбрать 0 женщин – это выбрать 6 из 7 мужиков ( ). Выбрать одну женщину – это выбрать 5 из 7 мужиков и 1 из 4 женщин ( ). Итого получаем: - - = 371

3) На каждой кости – т.е. на обоих двух сразу выпало 3, 4, 5 и 6 очков. Это 16 вариантов. Вероятность равна 16*(1/36) = 4/9.

4) Хотя бы одному – это от 1 до 4 парням достанутся билеты. Всего у нас вариантов распределения. Проще посчитать количество вариантов, когда билеты достаются только девушкам, и отнять их от общего количества, чтобы получить количество вариантов с парнями. После этого по формуле классической вероятности находим вероятность того, что хотя бы одному парню достанется билет, разделив количество комбинаций с парнями на общее их количество.

Количество вариантов только с девушками - 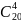. Находим количество комбинаций с парнями: - = 10105. Находим вероятность того, что билет достанется хотя бы одному парню: 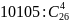= 0.6759.

5) Вроде формула Байеса, но считается это все как сумма произведений соответствующих процентов, т.е. процент местных авиалиний умножить на процент бизнесменов на них плюс процент авиалиний по СНГ умножить на процент бизнесменов на них плюс процент международных рейсов умножить на процент бизнесменов на них: 0.6*0.5 + 0.3*0.6 + 0.1*0.9 = 0.57. Смысл в том, что нужно найти общий процент бизнесменов, путешествующих всеми авиарейсами.

6) Биномиальный закон распределения. МХ = np = 0.2*2 = 0.4.

P(0) = 0.8² = 0.64

P(1) = 2*0.2*0.8 = 0.32

P(2) = 0.2² = 0.04

7) Неравенство Маркова. MX = 45*0.8 = 36. Р(Х>30) < MX/ξ; P < 1.2. Мб я уже закипел, но вероятность равняется единице (в чем очень сомневаюсь).

8) Вероятность выпадения герба равна 0.5, вероятность невыпадения – 0.5. Найдем размер отклонения: 60*0.1 = 6. Найдем DX = 0.5*0.5*60 = 15. Подставим значения в формулу:

P(|X-MX|<6) > 1 – (15/6²); P > 7/12.