Примечание: ленился ставить знак «больше/меньше или равно» в неравенствах.

Вариант 20

1. а) 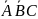+ + 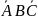б) AB + BC + AC

2. 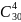= = 27405

3. Всего вариантов выпадения костей 6³ (три кости, по 6 вариантов у каждой). Из них вариантов выпадения одинаковых очков всего шесть – три единицы, три двойки и т.д. Делим количество благоприятных вариантов на общее их количество, получаем 6/6³ = 1/36.

4. Считаем количество возможных рассадок для каждого вагона как * * :

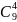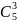* * = 1260

Считаем общее количество рассадок как 3⁹, т.к. у нас 9 человек, и у каждого есть выбор из трех вагонов. Т.е. первый может выбрать любой из трех, второй любой из трех, и т.д. Потому мы перемножаем варианты выбора каждого человека, получаем 19683. Для нахождения вероятности искомой комбинации пользуемся формулой классической вероятности m/n, где m = 1260, n = 19683. P = 0.064.

5. Переложить мы можем либо 1 черный, один белый, либо 2 черных, либо два белых. Для начала нам нужно найти вероятность для каждого из этих вариантов. Вероятность того, что вытащим:

1 черный и 1 белый: 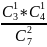= 4/7

Два белых: 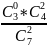= 2/7

Два черных: 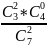= 1/7

Теперь посчитаем для каждого итога вероятность достать белый шар из второй урны без учета посчитанных выше вероятностей перекладывания (потом пригодятся). Если переложили 1 белый и 1 черный, то в урне стало 6 шаров обоих цветов, следовательно, вероятность достать белый шар равна 6/(6+6) = 0,5. Если переложили два черных, то в урне стало 5 белых и 7 черных шаров. Вероятность равна 5/(5+7) = 5/12. Если переложили 2 белых, то в урне 7 белых и 5 черных, вероятность равна 7/(7+5) = 7/12.

А теперь находим итоговую вероятность достать белый шар из урны. Для этого вероятность каждого варианта перекладывания нужно перемножить с вероятностью достать белый шар при таком раскладе из второй урны, а потом сложить три произведения:

4/7*1/2 + 1/7*5/12 + 2/7*7/12 = 43/84

6. p(0) = 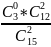= 22/35 p(1) = 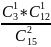= 12/35 p(2) = 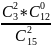= 1/35

7. Найдем MХ как np и применим неравенство Маркова: Р(X > ξ) < МX/ξ

P(X > 20)<(0,75*25)/20; P < 0,9375

8. σ < 4 => DX < 16. Применим теорему Чебышева, т.к. в условии фигурируют непонятные слова типа среднего арифметического случайных величин и среднего арифметического их математических ожиданий. Знаков < возле дисперсии и квадратического отклонения не пугаемся, а берем максимальное значение и того, и того.

P(|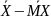 |< ε) > 1 – DX/n ε²; P > 0,97

Вариант 2

1. а) + + б) 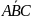в) АВ +АС +ВС

2. * = 1680

3. Сумма должна равняться 9, 10, 11, 12. Это следующие комбинации: 3-6, 4-5, 5-4, 6-3; 4-6, 5-5, 6-4; 5-6, 6-5; 6-6. Всего 10 комбинаций. Вероятность выпадения одной комбинации – 1/36, следовательно, вероятность выпадения более 8 очков = 10/36 = 5/18.

4. Хотя бы один банк – это сумма вероятностей банкротства 1 из 3, 2 из 3 и 3 из 3. Считать все это долго, потому пойдем от обратного: найдем вероятность сохранения всех банков, а потом отнимем ее от единицы: 1 - 0.75*0.8*0.95 = 0.43

5. Сначала находим вероятности совместных событий – достать определенную винтовку и при этом из нее попасть, а потом складываем их. Вероятность достать оптику или не оптику – 0.5. Вероятность поражения мишени: 0.5*0.9+0.5*0.7=0.8

6. p(0) = 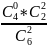= 1/15 p(1) = 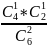= 8/15 p(2) = = 6/15 = 2/5 MX = 2*4/6 = 4/3

7. Нормальный закон распределения: а = 50 мм, DX = 4 мм², σ = 2 мм, α = 45 мм, β = 55 мм.

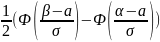= (Ф(2.5) + Ф(2.5)) = 0.98758

8. Даже сказали, что использовать, следовательно, хватит простого знания формулы. Согласен с комментарием под фото в альбоме группы : )

P(|X-MX|<3)>1-(npq/3²); P>29/45

Вариант 7

1. а) А+В+С б) + +

2. Один цвет из пяти у нас красный, осталось четыре цвета. Красный цвет на трехполосном флаге может располагаться в трех местах. Остальные два места занимают любые из оставшихся четырех цветов. Тогда количество комбинаций находится путем перемножения количества цветов, которые могут стоять на каждом месте для каждого случая постановки красного цвета, а потом складываются. 1*4*3 – если первый цвет красный, то второй – один из четырех, второй – один из трех оставшихся. 4*1*3 – если красный на втором, 4*3*1 – если на третьем. Складываем, получаем итого 36 комбинаций.

3. Благоприятствующие комбинации: 1-2, 2-4, 3-6, 2-1, 4-2, 6-3, всего шесть. Вероятность для одной комбинации – 1/36, следовательно, вероятность искомого события – 1/6.

4. Р = 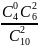= 1/3

5. Оформляем по формуле Байеса. Р(Н₁) = 0.3, Р(Н₂) = 0.5, Р(Н₃) = 0.2. Р(А/Н₁) = 0.01, Р(А/Н₂) = 0.03, Р(А/Н₃) = 0.1. Нас интересует Р(Н₁/А) – вероятность того, что Петров относится к водителям категории А. По формуле Байеса:

Р(Н₁/А) = 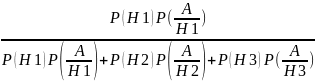= 3/38

6. Решаем с помощью формулы Байеса. Берем за m количество пройденных светофоров, 0, 1, 2, 3, n = 3.

Х	0	1	2	3
Р	0.125	0.375	0.375	0.125

7. Равномерный закон распределения. р(Х) = 1/60, умножим на 20, получим искомую вероятность в 1/3.

8. Считаем по неравенству Маркова.

P(X< ξ)>1-MX/ ξ;

1 - MX/ξ = 0.9; 0.1 = MX/ξ; ξ = 250. Следовательно, можно ожидать скорость ветра от 0 км/ч до 250 км/ч. Нереальные значения, но другие получить не удалось : )

Вариант 18

1. а) АВ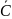 + А С + ВС б) А + В + С

2. Для нахождения полной вероятности рассмотрим случаи, когда А стоит на 1, 2, 3, 4 месте, а Б – на местах после А для каждого из случаев.

А на первом: Б на втором - 1*1*3*2*1 = 6 комбинаций; Б на третьем – 1*3*1*2*1 = 6 комбинаций; Б на четвертом – 6 комбинаций, Б на пятом – 6 комбинаций. А на втором: Б на третьем – 3*1*1*2*1 = 6 комбинаций; Б на четвертом – 3*1*2*1*1 = 6 комбинаций; Б на пятом – 3*1*2*1*1 = 6 комбинаций. А на третьем: Б на четвертом – 3*2*1*1*1 = 6 комбинаций; Б на пятом – 3*2*1*1*1 = 6 комбинаций. А на четвертом, Б на пятом: 3*2*1*1*1 = 6 комбинации. Складываем, получаем 60 комбинаций.

3. Находим вероятность того, что выпадет 4, 5 или 6 на какой-либо из костей. 4-4, 4-5, 4-6; 5-4, 5-5, 5-6, 6-4, 6-5, 6-6 – всего 9. Вероятность 0.25.

4. Биномиальный закон распределения. Вероятность рождения в определенный день – 1/7, вероятность неуспеха соответственно 6/7. Найдем вероятность того, что два из трех родились в четверг, вероятность того, что один из трех родился в пятницу и перемножим.

P(2) = 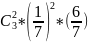= 3*(1/49)*(6/7) = 18/343; P(1) = = 3*(1/7)*(36/49) = 108/343; P(2)*P(1)= 0.017.

5. Формула Байеса. (0.75*0.6)/((0.75*0.6+0.25*0.9)) = 2/3.

6. МХ = 2*4/15 = 8/15.

Р(0) = 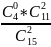= 11/21 р(1) = = 44/105 р(2) = 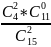= 2/35

7. МХ = 8000*0.6 = 4800. DX = 8000*0.6*0.4 = 1920. σ = 43,8. Нужно найти максимальное число книг, потому левая граница α равна нулю, нужно найти правую границу β.

0.9 = 0.5(Ф(β-а)/σ) – Ф(-а/σ)); 1.8 = Ф(t) + 1; Ф(t) = 0.8; t = 1.28; (β-4800)/43.8 = 1.28; β = 4856

8. Неравенство Маркова. Р(Х<300)>1-200/300; P>1/3.