Заняття 5 встановлення закону розподілу випадкової величини

Мета завдання – необхідно перевірити гіпотезу про те, що випадкова величина розподілена за показниковим законом.

Вирішення:

Таблиця 5.1 – Вибірка значень випадкової величини

3	36	42	48	30	62	50	99	276	42
4	44	96	126	40	186	110	50	210	50
9	39	86	106	90	219	170	42	6	99
12	72	162	192	120	132	20	147	96	222
10	50	45	255	100	110	125	74	184	112
18	108	48	288	180	198	310	81	252	258
21	201	94	54	210	231	35	342	69	321
24	114	234	54	240	264	90	141	32	144
18	138	178	198	180	138	445	112	188	38
30	60	297	117	330	33	95	102	303	300

Таблиця 5.2 – Статистична обробка обсягів вантажів по скаладах

№ з/п	Границя інтервалів	Частота	Середина інтервалів	Частість	Довжина інтервалів	Щільність		Ф-я розподілу
						емпір.	теор.	емпір.	теор.
	Qi	Mn	Qm	Rn	Hn	Pn	F*(Qn)	F*(Qn)	F(Qn)
1	2	3	4	5	6	7	8	9	10
1	0;56	33	28	0,33	56	6	6,4	0,33	0,2
2	56;112	23	84	0,23	56	4	4	0,56	0,5
3	112;168	12	140	0,12	56	2	2,64	0,68	0,67
4	168;224	15	196	0,15	56	2,7	1,6	0,83	0,8
5	224;280	8	252	0,08	56	1,4	1,08	0,91	0,865
6	280;336	7	308	0,07	56	1,25	0,696	0,98	0,913
7	336;392	1	364	0,01	56	0,2	0,44	0,99	0,945
8	392;448	1	420	0,01	56	0,2	0,288	1	0,964

h ≈ 56 – ширина інтервалу.

Визначимо математичне очікування:

a = M[T] = ∑ t_ip_i = 0,12432

Функція розподілу величини:

;

λ = 1/a = 1 / 0,12432 = 8

Щільність розподілу вантажів:

f(Q) =

Обчислимо значення щільності розподілу для заданих середин інтервалів (гр.4) і занесемо в таблицю (гр. 8).

f(0,028) = 6,4;

f(0,084) = 4;…

Гістограма розподілу вантажів по складах і теоретична щільність ймовірності розподілу показані на рис 1.1.

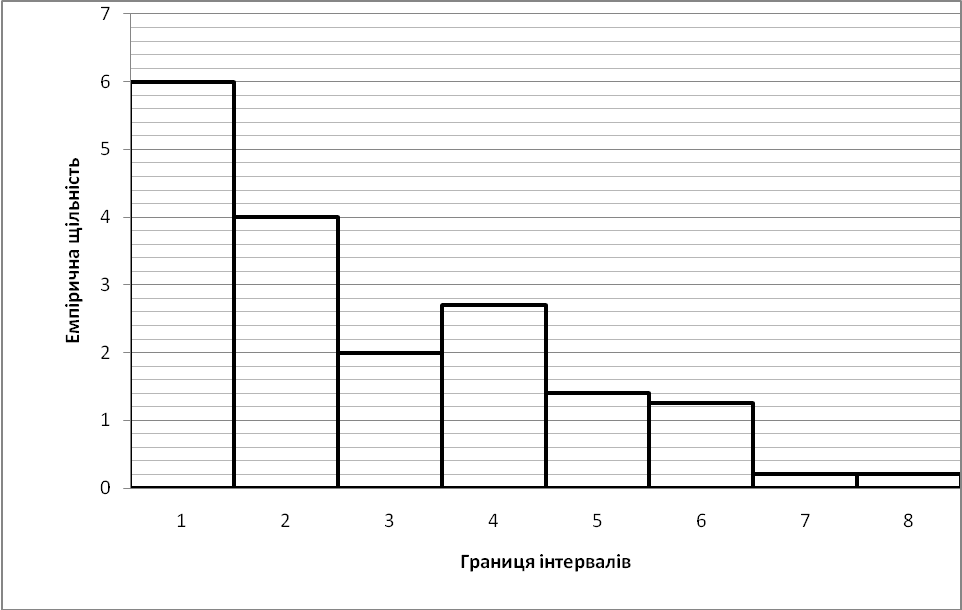
Визначимо міру розбіжності:

χ² = 9,405

Показниковий розподіл є однопараметричним, а в зв’язку з об’єднанням двох інтервалів загальна кількість зв’язків дорівнює 7, тобто кількість зв’язків складає

r = k - S – 1= 8- 1- 1=6

Для r=6 обчислена міра χ² = 9,405 лежить в межах від 0,1 до 0,2, що значно більше допустимої 0,05.

Таким чином, розподіл вантажів по складах узгоджується з показниковим законом.

Визначаємо узгодженість теоретичного і емпіричного розподілів за критерієм Колмогорова. Для цього побудуємо статистичний p_n^*(Q_n) і теоретичний розподіли за гр.. 9,10.

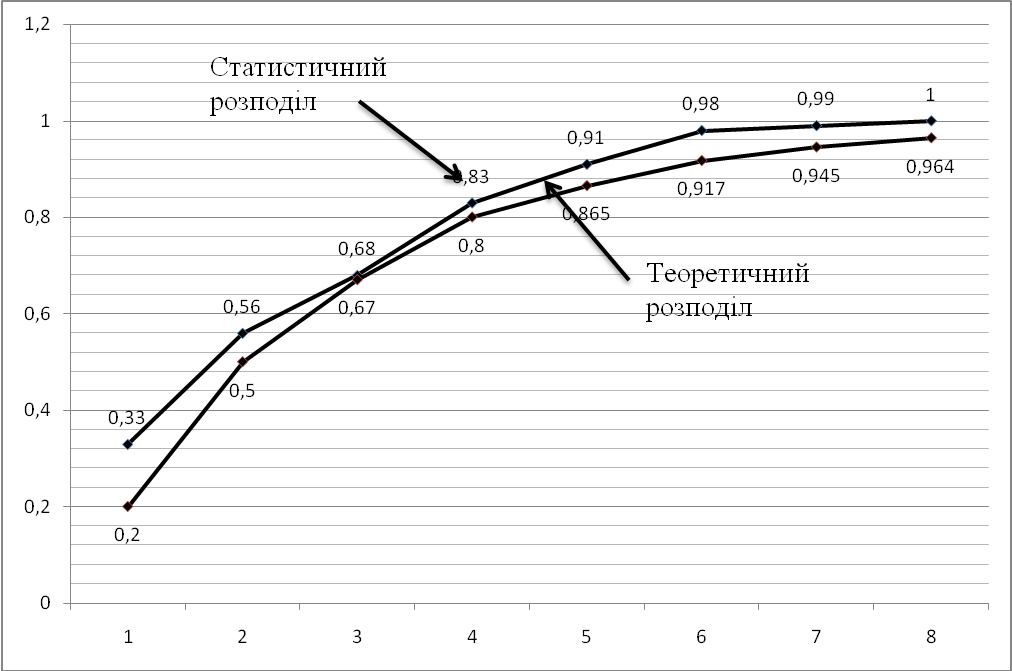
Обчислимо для кожного інтервалу ймовірність попадання в нього випадкової величини як добуток щільності на довжину інтервалу, а потім їх послідовно просумуємо.

F^*(0,028) = 6 ∙ 0,056 = 0,33

F^*(0,028)= 0,56

Аналогічно обчислюють теоретичну функцію розподілу.

Відмітимо, ща за рахунок неточності розрахунку (табл. 2), гр. 9-10) виходить незначне відхилення накопичених значень теоретичної функції (F^*=0,964) від одиниці.

Визначимо міру розбіжності між теоретичним і емпіричним розподілом як модуль між емпіричною функцією розподілу F^*(Q_n) і відповідної теоретичної D = k₀ (рис.2)

k₀ = 0,33 – 0,2 = 0,13

Обчислимо параметр:

λ = k₀ ∙ 10 = 1,3

Знаходимо, що розподіл вантажів узгоджується з показниковим законом.

Висновки.

В результаті проведених розрахунків була підтверджена гіпотеза, що випадкова величина розподілена за показниковим законом. Відмітимо, ща за рахунок неточності розрахунку (табл. 2), гр. 9-10) виходить незначне відхилення накопичених значень теоретичної функції (F^*=0,964) від одиниці, але це не впливає на результат.

28