Заняття 4 розрахунок матриці пасажирських кореспонденцій гравітаційним методом
Мета заняття – вивчити методику розрахунку матриці пасажирських кореспонденцій гравітаційним методом.
Завдання. Визначити матрицю пасажирських кореспонденцій гравітаційним методом.
Вказівки до виконання завдання
Відповідно до заданого варіанта оформляємо вихідні дані у табл. 4.1.
Таблиця 4.1 – Вихідні дані
Номер транспортного району |
Номер транспортного району за варіантом |
Мешкає, тис. чол. |
Працює, тис. чол. |
Координата |
|
X |
Y |
||||
1 |
1 |
6 |
1 |
40 |
54 |
2 |
9 |
57 |
12 |
4 |
98 |
3 |
16 |
99 |
11 |
98 |
85 |
4 |
35 |
82 |
37 |
80 |
23 |
5 |
40 |
99 |
33 |
31 |
46 |
6 |
58 |
50 |
18 |
83 |
25 |
7 |
61 |
43 |
19 |
41 |
60 |
8 |
50 |
14 |
6 |
19 |
89 |
9 |
76 |
12 |
5 |
15 |
73 |
10 |
84 |
53 |
11 |
3 |
73 |
|
|
|
|
|
|
Вирішення:
1. Нарисуємо в масштабі 1:100000 координатну модель транспортної мережі. (див. рис. 1).
2. Шляхом вимірювання за координатною моделлю транспортної мережі найдемо найкоротшу довжину пересування між районами lij. (табл. 4.2.).
Таблиця 4.2 – Матриця найкоротших шляхів, км.
Номер району відправлення |
Номер району прибуття |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
0 |
5,9 |
7,1 |
5,0 |
1,4 |
5,7 |
0,5 |
4,3 |
3,4 |
4,4 |
2 |
5,9 |
0 |
9,7 |
11 |
6,4 |
11,7 |
5,3 |
1,8 |
2,6 |
2,4 |
3 |
7,1 |
9,7 |
0 |
7,5 |
8,3 |
6,8 |
6,5 |
8,1 |
9,5 |
10,5 |
4 |
5,6 |
11 |
7,5 |
0 |
5,3 |
0,8 |
5,6 |
9,3 |
8,6 |
9,6 |
5 |
1,4 |
6,4 |
8,3 |
5,3 |
0 |
6,6 |
1,9 |
5,6 |
4,0 |
5,0 |
6 |
4,6 |
3,3 |
5,4 |
4,2 |
5,7 |
0 |
7,7 |
6,4 |
6,7 |
10 |
7 |
6,7 |
4,4 |
2,3 |
3,5 |
6,8 |
7,7 |
0 |
1,3 |
4,1 |
4 |
8 |
6,8 |
3,1 |
1 |
2,2 |
5,4 |
6,4 |
1,3 |
0 |
3,5 |
4,4 |
9 |
4,1 |
6,6 |
4,5 |
5,7 |
2,7 |
6,7 |
4,1 |
3,5 |
0 |
1 |
10 |
2,9 |
2,6 |
3,8 |
3,5 |
4,3 |
1,7 |
6,1 |
4,8 |
7 |
0 |
3. Визначимо з використанням формул час руху між транспортними районами і трудність сполучення. При розрахунку швидкість руху транспортного засобу приймаємо 20 км/год.
Наприклад, час руху між першим та другим районами дорівнює:
Пересування у середині району (t11=t22=…=t10,10=2хв.). Результати розрахунків наведено в табл. 4.3
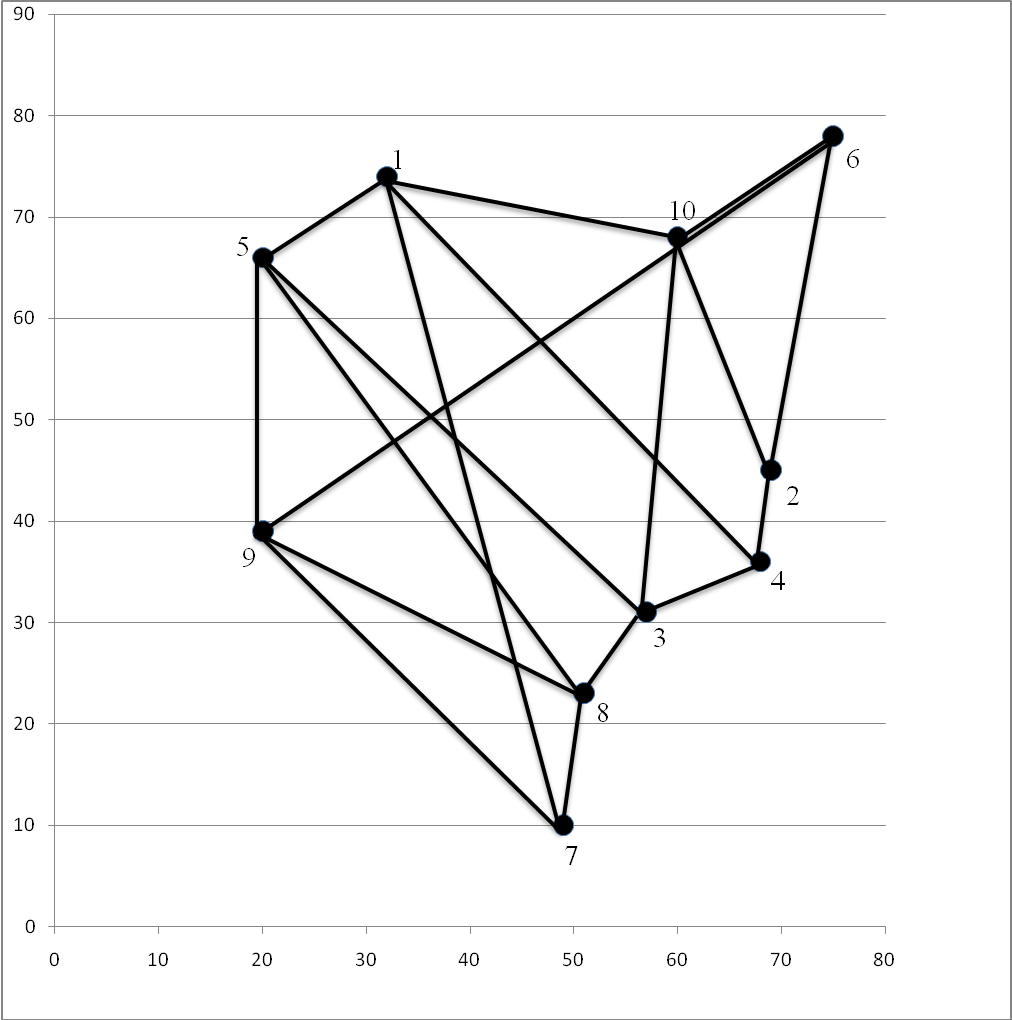
Рис. 2 – Графічне відображення транспортної мережі
Таблиця 4.3 – Час руху між транспортними районами, хв.
Номер району відправлення |
Номер району прибуття |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
2 |
17,7 |
21,3 |
1,5 |
4,2 |
17,1 |
1,5 |
12,9 |
10,2 |
13,2 |
2 |
17,7 |
2 |
29,1 |
33 |
19,2 |
35,1 |
15,9 |
5,4 |
7,8 |
7,2 |
3 |
21,3 |
29,7 |
2 |
22,5 |
24,9 |
20,4 |
19,5 |
24,3 |
28,5 |
31,5 |
4 |
4,5 |
33 |
22,5 |
2 |
15,9 |
2,4
|
16,8 |
27,9 |
25,8 |
28,8 |
5 |
4,2 |
19,2 |
2,9 |
15,9 |
2 |
19,8 |
5,7 |
16,8 |
12 |
15 |
6 |
17,1 |
35,1 |
26,4 |
2,4 |
19,8 |
2 |
18,6 |
29,1 |
27,6 |
30 |
7 |
1,5 |
15,9 |
16,8 |
16,8 |
5,7 |
18,6 |
2 |
11,1 |
9 |
12 |
8 |
12,9 |
5,4 |
24,3 |
27,9 |
16,8 |
29,1 |
11,1 |
2 |
12,6 |
13,2 |
9 |
10,2 |
7,8 |
25,5 |
25,8 |
12 |
27,6 |
9 |
12,6 |
2 |
3 |
10 |
13,2 |
7,2 |
21,5 |
28,8 |
15 |
30 |
12 |
13,2 |
3 |
2 |
Наприклад, трудність сполучення для першого транспортного району дорівнює:
Результати розрахунків наведено в табл. 4.4.
Таблиця 4.4 – Трудність сполучення між транспортними районами
Номер району відправлення |
Номер району прибуття |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
0,5 |
0,06 |
0,05 |
0,07 |
0,24 |
0,06 |
0,07 |
0,08 |
0,1 |
0,08 |
2 |
0,06 |
0,5 |
0,03 |
0,03 |
0,05 |
0,03 |
0,06 |
0,18 |
0,12 |
0,14 |
3 |
0,05 |
0,03 |
0,5 |
0,04 |
0,04 |
0,04 |
0,05 |
0,04 |
0,03 |
0,03 |
4 |
0,07 |
0,03 |
0,04 |
0,5 |
0,06 |
0,42 |
0,06 |
0,04 |
0,04 |
0,03 |
5 |
0,238 |
0,048 |
0,064 |
0,055 |
0,5 |
0,058 |
0,049 |
0,062 |
0,123 |
0,078 |
6 |
0,06 |
0,03 |
0,04 |
0,42 |
0,05 |
0,5 |
0,05 |
0,03 |
0,04 |
0,03 |
7 |
0,07 |
0,06 |
0,05 |
0,06 |
0,17 |
0,05 |
0,5 |
0,09 |
0,11 |
0,08 |
8 |
0,08 |
0,8 |
0,04 |
0,04 |
0,06 |
0,03 |
0,09 |
0,5 |
0,08 |
0,08 |
9 |
0,1 |
0,12 |
0,03 |
0,04 |
0,08 |
0,04 |
0,11 |
0,08 |
0,5 |
0,3 |
10 |
0,08 |
0,14 |
0,03 |
0,03 |
0,07 |
0,03 |
0,08 |
0,08 |
0,3 |
0,5 |
4. Визначимо місткість транспортних районів.
За формулою визначимо трудову ємкість районів (кількість прибуття) (Нj):
Результати розрахунків занесені до табл. 4.9.
З використанням формули розрахуємо селітебну ємкість районів:
Результати розрахунків занесені до табл. 4.5.
Перевіримо
умову балансу ємкості транспортних
районів:
.
Таблиця 4.5 – Місткість транспортних районів.
Номер транспортного району |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Усього |
Селітебна ємкість району (Нi), тис. чол. |
15,17 |
0,233 |
19,61 |
11,9 |
20,77 |
8,4 |
7,47 |
4,67 |
2,1 |
20,07 |
110,4 |
Трудова ємкість району (Нj), тис. чол. |
16 |
0,8 |
31,8 |
20 |
20,8 |
0,8 |
0,8 |
0,8 |
0,8 |
1,8 |
110,4 |
5 Розрахунок матриці кореспонденцій.
Визначення величини кореспонденцій між i-м та j-м транспортними районами виконуємо із застосуванням гравітаційної моделі (за відправленням).
Визначимо елементи матриці Y на першій ітерації. Значення коефіцієнта балансування на першій ітерації кj=1.Наприклад,
Результати розрахунків наведені в табл. 4.6.
Таблиця 4.6 – Значення елементів матриці Y на першій ітерації
Номер району відправлення |
Номер району прибуття |
|
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
1 |
8 |
0,048 |
1,64 |
1,26 |
4,95 |
0,057 |
0,04 |
0,039 |
0,06 |
1,93 |
18,032 |
2 |
0,096 |
0,4 |
5,215 |
7,4 |
0,998 |
0,8 |
0,06 |
0,086 |
0,04 |
3,15 |
17,246 |
3 |
0,8 |
0,127 |
16,4 |
5,56 |
1,33 |
0,049 |
0,116 |
0,266 |
0,059 |
1,478 |
26,187 |
4 |
1,008 |
0,296 |
9,118 |
10 |
1,144 |
0,063 |
0,076 |
0,122 |
0,464 |
1,596 |
23,953 |
5 |
3,808 |
0,038 |
2,1 |
1,1 |
10,4 |
0,046 |
0,039 |
0,049 |
0,098 |
1,31 |
18,99 |
6 |
1,152 |
0,8 |
2,03 |
1,58 |
1,21 |
0,4 |
0,344 |
0,042 |
0,04 |
3,293 |
10,89 |
7 |
0,8 |
0,6 |
4,756 |
1,9 |
1,02 |
0,344 |
0,4 |
0,205 |
0,648 |
0,924 |
11,597 |
8 |
0,784 |
0,086 |
10,9 |
3,04 |
1,290 |
0,042 |
0,205 |
0,4 |
0,076 |
1,159 |
17,98 |
9 |
1,296 |
0,04 |
2,42 |
1,16 |
2,558 |
0,04 |
0,065 |
0,076 |
0,4 |
0,806 |
8,8616 |
10 |
1,84 |
0,102 |
2,886 |
1,9 |
1,622 |
0,157 |
0,044 |
0,055 |
0,038 |
8,4 |
17,046 |
Розрахуємо кореспонденції між районами. Наприклад,
Результати розрахунків наведені в табл. 4.11. Перевіримо умови балансу матриці кореспонденцій, використовуючи формулу (4.9). Наприклад,
Результати розрахунків занесено у відповідний рядок табл. 4.7.
Таблиця 4.7 – Матриця кореспонденцій на першій ітерації, тис. чол.
Номер району відправлення |
Номер району прибуття |
|
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
1 |
6,73 |
0,04 |
1,379 |
1,06 |
4,165 |
0,048 |
0,034 |
0,033 |
0,545 |
1,625 |
15,17 |
2 |
0,001 |
0,005 |
0,07 |
0,1 |
0,013 |
0,01 |
0,001 |
0,001 |
0,001 |
0,029 |
0,233 |
3 |
0,599 |
0,095 |
12,28 |
4,16 |
0,996 |
0,037 |
0,087 |
0,199 |
0,044 |
1,107 |
19,61 |
4 |
0,5 |
0,147 |
4,56 |
4,97 |
0,568 |
0,314 |
0,038 |
0,06 |
0,23 |
0,79 |
11,9 |
5 |
4,16 |
0,04 |
2,297 |
1,2 |
11,37 |
0,05 |
0,4 |
0,542 |
0,108 |
1,433 |
20,77 |
6 |
0,889 |
0,617 |
1,566 |
1,219 |
0,933 |
0,31 |
0,266 |
0,032 |
0,031 |
2,54 |
8,4 |
7 |
0,515 |
0,386 |
3,063 |
1,224 |
0,657 |
0,22 |
0,258 |
0,132 |
0,417 |
0,595 |
7,47 |
8 |
0,204 |
0,022 |
2,83 |
0,790 |
0,33 |
0,011 |
0,033 |
0,104 |
0,12 |
0,3 |
4,67 |
9 |
0,307 |
0,009 |
0,573 |
0,275 |
0,61 |
0,009 |
0,015 |
0,018 |
0,095 |
0,191 |
2,1 |
10 |
2,166 |
0,121 |
3,397 |
2,237 |
1,91 |
0,185 |
0,052 |
0,065 |
0,045 |
9,89 |
20,07 |
|
16,08 |
1,486 |
32,02 |
17,24 |
21,56 |
0,913 |
0,845 |
0,696 |
1,045 |
18,5 |
– |
|
0,484 |
85,8 |
2,37 |
13,81 |
3,65 |
14,2 |
5,663 |
12,6 |
30,69 |
11,93 |
– |
%
Умова відповідності вихідної величини трудової ємкості районів і трудової ємкості, отримана у результаті розподілу кореспонденцій за гравітаційною моделлю, виконується тільки для третього і шостого транспортних районів. Тому розрахуємо нові значення коефіцієнта балансування і проведемо розрахунок матриці кореспонденцій на новій ітерації. Наприклад,
Значення коефіцієнта для транспортних районів на другій ітерації наведено в табл. 4.8.
Таблиця 4.8 – Значення коефіцієнта балансування на другій ітерації.
Номер транспортного району |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Значення kj |
0,995 |
0,54 |
1,02 |
1,16 |
0,965 |
0,976 |
0,946 |
1,14 |
0,765 |
0,91 |
Визначимо елементи матриці Y на другій ітерації. Наприклад,
Результати розрахунків наведені в табл. 4.9.
Таблиця 4.9 – Значення елементів матриці Y на другій ітерації.
Номер району відправлення |
Номер району прибуття |
|
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
1 |
7,96 |
0,026 |
1,68 |
1,46 |
4,78 |
0,05 |
0,038 |
0,045 |
0,05 |
1,75 |
17,84 |
2 |
0,96 |
0,215 |
5,34 |
8,59 |
0,96 |
0,07 |
0,057 |
0,1 |
0,03 |
1,95 |
18,27 |
3 |
0,8 |
0,068 |
16,8 |
6,45 |
1,28 |
0,04 |
0,11 |
0, 3 |
0,05 |
1,34 |
27,24 |
4 |
1,00 |
0,159 |
9,34 |
11,6 |
1,1 |
0,06 |
0,07 |
0,14 |
0,04 |
1,45 |
24,96 |
5 |
3,79 |
0,02 |
2,15 |
12,76 |
10,03 |
0,04 |
0,037 |
0,057 |
0,07 |
1,19 |
30,16 |
6 |
1,15 |
0,04 |
2,08 |
1,83 |
1,16 |
0,35 |
0,032 |
0,048 |
0,03 |
2,99 |
9,72 |
7 |
0,8 |
0,033 |
4,87 |
2,2 |
0,98 |
0,03 |
0,38 |
0,23 |
0,05 |
0,84 |
10,4 |
8 |
0,78 |
0,047 |
11,2 |
3,53 |
1,244 |
0,036 |
0,194 |
0,458 |
0,06 |
1,05 |
18,58 |
9 |
1,29 |
0,022 |
2,49 |
1,35 |
2,5 |
0,035 |
0,06 |
0,87 |
0,3 |
0,73 |
9,616 |
10 |
1,83 |
0,055 |
2,96 |
2,2 |
1,57 |
0,137 |
0,04 |
0,063 |
0,03 |
7,63 |
16,51 |
Розрахуємо кореспонденції між районами. Наприклад,
Результати розрахунків наведені в табл. 4.10.
Таблиця 4.10 – Матриця кореспонденцій на другій ітерації, тис. чол.
Номер району відправлення |
Номер района прибуття |
|
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
1 |
6,78 |
0,02 |
1,43 |
1,24 |
4,06 |
0,04 |
0,03 |
0,038 |
0,04 |
1,5 |
15,17 |
2 |
0,01 |
0,003 |
0,07 |
0,11 |
0,01 |
0,001 |
0,001 |
0,001 |
0,001 |
0,02 |
0,233 |
3 |
0,57 |
0,049 |
12,1 |
4,64 |
0,92 |
0,03 |
0,08 |
0,22 |
0,03 |
0,97 |
19,61 |
4 |
0,48 |
0,076 |
4,45 |
5,53 |
0,53 |
0,026 |
0,034 |
0,066 |
0,017 |
0,69 |
11,9 |
5 |
2,6 |
0,014 |
1,48 |
8,79 |
6,91 |
0,028 |
0,026 |
0,039 |
0,052 |
0,82 |
20,77 |
6 |
0,99 |
0,038 |
1,8 |
1,58 |
1,006 |
0,3 |
0,028 |
0,04 |
0,026 |
2,58 |
8,4 |
7 |
0,57 |
0,023 |
3,5 |
1,58 |
6,7 |
0,02 |
0,27 |
0,168 |
0,036 |
0,6 |
7,47 |
8 |
0,196 |
0,011 |
2,8 |
0,89 |
0,31 |
0,01 |
0,049 |
0,115 |
0,015 |
2,26 |
4,67 |
9 |
0,28 |
0,005 |
0,5 |
0,29 |
0,54 |
0,008 |
0,013 |
0,19 |
0,067 |
0,16 |
2,1 |
10 |
2,226 |
0,067 |
3,6 |
2,68 |
1,903 |
0,167 |
0,051 |
0,07 |
0,036 |
9,27 |
20,07 |
|
14,71 |
0,31 |
31,76 |
27,34 |
16,9 |
0,64 |
0,584 |
0,955 |
0,323 |
16,87 |
– |
% |
8,06 |
61,4 |
3,16 |
36,7 |
18,7 |
20,3 |
27 |
19,4 |
59,6 |
0,4 |
– |
Перевіримо умови балансу матриці кореспонденцій. Наприклад,
Результати розрахунків занесені у відповідний рядок табл. 4.10.
Розподіл кореспонденцій по транспортних районах на другій ітерації задовольняє умові (4.10), тому на цьому розрахунок матриці кореспонденції завершуємо.
6 Висновок.
Визначено матриці пасажирських кореспонденцій гравітаційним методом на першій і другій ітерації. Умова відповідності вихідної величини трудової ємкості районів і трудової ємкості, отримана у результаті розподілу кореспонденцій за гравітаційною моделлю, виконується тільки для першого, третього , п’ятого і сьомого транспортних районів. Тому було розраховано нові значення коефіцієнта балансування і проведено розрахунок матриці кореспонденцій на новій ітерації. В результаті розрахунків умова відповідності виконується для першого, третього і десятого транспортних районів.