
- •1. Теоретические вопросы темы «пр"ямоугольный треугольник»
- •1.2 Прямоугольный треугольник и его свойства
- •1°. Сумма двух острых углов прямоугольного треугольника равна 90°.
- •2°. Катет прямоугольного треугольника, лежащего против угла в 30º, равен половине гипотенузы.
- •1.3 Признаки равенства прямоугольных треугольников
- •1.4 Теорема Пифагора
- •Катеты в квадрат возводим,
- •И таким простым путем к результату мы придем.
- •1.6 Подобие прямоугольных треугольников
- •2. Методические основы изучения темы «Прямоугольный треугольник»
- •2.1 Психолого-педагогический аспект изучения темы
- •2.2 Управление учебным процессом при изучении темы «Прямоугольный треугольник» в курсе девятилетней школы
- •2.4 Два подхода к решению прямоугольных треугольников
- •2.5 Организация повторения изученного материала
- •.6 Нетрадиционная форма традиционного контроля
- •Карточка а
- •Ход урока:
- •Закрепление.
- •1. Назовите равенство, используя теорему Пифагора.
- •Нашел же рыбак его
- •Итоги урока:
- •Самоанализ урока.
1.6 Подобие прямоугольных треугольников
В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например, футбольный и теннисный мячи, круглая тарелка и большое круглое блюдо. В геометрии фигуры одинаковой формы принято называть подобными. Введём понятие подобных треугольников.
Пусть у двух треугольников ABC и A1B1C1 углы соответственно равны: <A=<A1, <B=<B1, <C=<C1. В этом случае стороны AB и A1B1, BC и B1C1, CA и C1A1 называются сходственными.
Два треугольника называются подобными, если их углы равны и стороны одного треугольника пропорциональны сходственным сторонам другого (рис. 15).
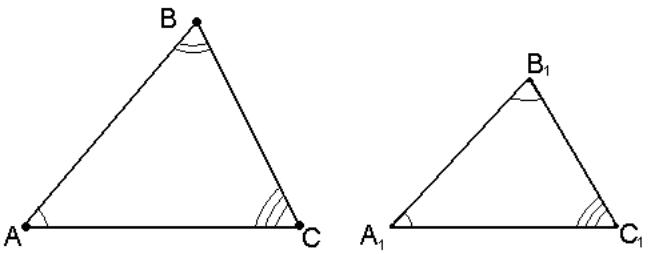
![]()
Другими словами, два треугольника подобны, если для них можно ввести обозначения ABC и A1B1C1 так что
<A=<A1, <B=<B1, <C=<C1, (1)
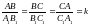 (2).
(2).
Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия. Обозначается ∆ABC~∆A1B1C1.
Оказывается, что подобие треугольников можно устанавливать, проверив только некоторые из равенств (1) и (2).
У прямоугольного треугольника один угол прямой. Поэтому для подобия прямоугольных треугольников достаточно, чтобы у них было по равному острому углу.
С помощью этого признака подобия прямоугольных треугольников докажем некоторые соотношения в треугольниках.
Пусть ABC - прямоугольный треугольник с прямым углом C. Проведём высоту CD из вершины прямого угла (рис. 16).
Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет его на подобные прямоугольные треугольники, каждый из которых подобен данному треугольнику.
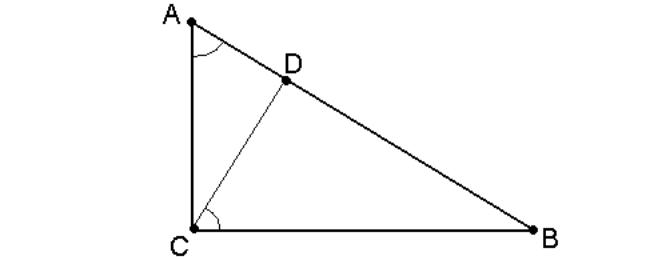
![]()
На рисунке ABC - прямоугольный треугольник <ABC=90º, CD ┴AB.
Δ ACD ~ Δ CDB;
Δ ACD ~ Δ ABC;
Δ CDB ~ Δ ABC.
Треугольники ABC и CBD имеют общий угол при вершине B. Следовательно, они подобны ∆ABC~∆ CBD. Из подобия треугольников следует пропорциональность соответствующих сторон:
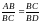 ,
или
,
или
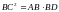 ,
а отсюда следует, что
,
а отсюда следует, что
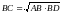 .
Это соотношение обычно формулируется
так: катет
прямоугольного треугольника есть
среднее пропорциональное между
гипотенузой и проекцией этого катета
на гипотенузу.
.
Это соотношение обычно формулируется
так: катет
прямоугольного треугольника есть
среднее пропорциональное между
гипотенузой и проекцией этого катета
на гипотенузу.
Прямоугольные треугольники ACD и CBD также подобны. У них равные острые углы при вершинах A и C. Из подобия этих треугольников следует пропорциональность их сторон:
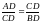 или
или
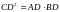 ,
а отсюда следует, что
,
а отсюда следует, что
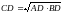 .
Это соотношение обычно формулируется
так: высота
прямоугольного треугольника, проведённая
из вершины прямого угла, есть среднее
пропорциональное между проекциями
катетов на гипотенузу.
.
Это соотношение обычно формулируется
так: высота
прямоугольного треугольника, проведённая
из вершины прямого угла, есть среднее
пропорциональное между проекциями
катетов на гипотенузу.
2. Методические основы изучения темы «Прямоугольный треугольник»
Методика обучения математике не только логически организует отобранный материал, но и ориентирует его на особенности учащихся того или иного класса, используя закономерности памяти, мышления, внимания и т.д., индивидуальные способности возрастной группы.
Основная роль учителя математики в современных условиях - это воспитание личности учащихся, формирование их потребностно - мотивационной сферы, воспитание их способностей, нравственных идеалов и убеждений. Обучение знаниям, умениям и навыкам по математике является составной частью этого воспитания и тем процессом, в котором это воспитание осуществляется.
Обучение математике способствует становлению и развитию нравственных черт личности: настойчивости и целеустремлённости, познавательной активности и самостоятельности, дисциплины и критического мышления, способности аргументировано отстаивать свои взгляды и убеждения. Изучение математики вносит определенный вклад в эстетическое воспитание человека, формируя понимание красоты и изящества математических убеждений, способствуя восприятию геометрических форм и симметрии. Изучение математики развивает воображение и пространственные представления.
