Введение

Образование на современном этапе характеризуется усилением внимания к ученику, к его саморазвитию и самопознанию, вниманием ученика к окружающему миру и к себе, к воспитанию умения искать и находить своё место в жизни. Целью современного образования является полное достижение развития тех способностей личности, которые нужны ей и обществу.

Цели обучения математике в общеобразовательной школе определяются её ролью в развитии общества в целом и формировании личности каждого отдельного человека.

В последнее время много говорится о недостаточной эффективности процесса обучения в школе, поскольку традиционная организация не отвечает требованиям времени, не создаёт условий для улучшения качества обучения и развития учащихся.

Образовательные и воспитательные задачи обучения математике должны решаться комплексно с учётом возрастных особенностей учащихся, специфики математики как науки и учебного предмета, определяющей её роль и место в общей системе школьного обучения и воспитания. Учителю предоставляется право самостоятельного выбора методических путей и приёмов решения этих задач.

Среди различных разделов математики, изучаемых в школе, особое место занимает и играет особую роль - геометрия. Возрастание значимости геометрии на всех ступенях образовательной лестницы, в самых разных областях науки, техники, искусства - заметная тенденция сегодняшнего времени. Среди всех предметов математического цикла (и не только математического) именно геометрия обладает самым большим развивающим потенциалом. Занятия геометрией могут помочь способному ребёнку максимально ускорить темпы своего интеллектуального развития.

Геометрия развивает логическое мышление, которое является одним из важнейших элементов воспитания личности, а также нравственное воспитание, независимость суждений и поведения.

Однако следует признать, что за последние годы уровень геометрической подготовки значительно снизился и достиг минимальной отметки, чуть ли не за всю историю существования школьной геометрии.

Геометрия, элементы которой возникли в глубокой древности из практических запросов людей, является в тоже время продуктом естественной потребности человека в познании, постоянном стремлении его к совершенству и красоте. Но вместе с тем, её относят к одному из самых трудных и, возможно из-за этого нелюбимых предметов.

Издревле, в связи с необходимостью измерять расстояния, площади земельных участков, возводить постройки, изготовлять орудия труда и предметы обихода. Слово «Геометрия» - греческое, в переводе на русский язык оно означает «землемерие». Сейчас геометрия не ограничивается задачами «землемерия». Её методы и выводы проникли во многие области человеческой деятельности.

Процесс накопления человечеством геометрических сведений был очень длительным и осуществлялся в разнообразных формах. Первоначально единственным источником этих сведений был опыт, наблюдения над свойствами линий, поверхностей и тел. Получение геометрических сведений чисто опытным путём потребовало очень большого времени.

Целью изучения курса геометрии в 7-9 классах является систематическое изучение свойств геометрических фигур на плоскости, развитие логического мышления и подготовки аппарата, необходимого для изучения смежных дисциплин (физика, черчение и т.д.) и курса стереометрии старших классах.

Курс характеризуется рациональным сочетанием логической строгости и геометрической наглядности. Увеличивается теоретическая зависимость изучаемого материала, расширяются внутренние логические связи курса, повышается роль дедукции, степень абстрактности изучаемого материала. Учащиеся овладевают приемами аналитико-синтетической деятельности при доказательстве теорем и решении задач. Изложение материала характеризуется постоянным обращением к наглядности, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе. Целенаправленное обращение к примерам из практики развивает умения учащихся вычленять геометрические факты, формы и отношения в предметах и явлениях действительности, использовать язык геометрии для их описания.

Данная выпускная квалификационная работа посвящена теме «Прямоугольный треугольник», даны методические рекомендации к изучению данной темы.

Материал по освещаемой проходит через многие главы учебников в 7-8 классов, на различных этапах изучения школьного курса геометрии. При работе над данной темой были собраны все имеющиеся теоретические данные по теме «Прямоугольный треугольник», позволяющие ученикам лучше усвоить тему, опираясь на ранее изученный материал.

Так как тема изучения прямоугольного треугольника является начальной стадией геометрической науки, она должна быть представлена полностью, раскрыта и преподнесена доступно для учеников, дабы развить у учащихся изучать предмет геометрии.

В процессе изучения дальнейших материалов геометрии приходится неоднократно возвращаться к истокам начала науки, где находится материал, непосредственно связанный с прямоугольным треугольником; кроме того, учитель вынужден внедрять новые методы, разрабатывать эффективную методику обучения, так что представленная работа полностью освещает актуальность выбранной темы.

Целью исследования представленной работы является разработка методики обучения прямоугольных треугольников и, непосредственно, изучение и анализ прямоугольных треугольников.

Проблема исследования состоит в разработке методических рекомендаций к теме «Прямоугольный треугольник», в связи с огромной значимостью данной темы в курсе геометрии.

Объектом исследования является процесс обучения геометрии в основной школе.

Предмет исследования - методика изучения свойств прямоугольного треугольника в средней школе, формирующая развитие у учащихся способностей к получению математических знаний.

Для успешной реализации поставленной цели необходимо решить следующие задачи исследования:

♦ провести анализ математической, методической и психолого-педагогической литературы;

♦ рассмотреть свойства прямоугольных треугольников и показать применение этих свойств к решению задач;

♦ показать практическую значимость темы;

♦ разработать методические рекомендации к изучению темы.

Методы исследования:

♦ анализ научной - математической, методической и психолого-педагогической литературы;

♦ систематизация и обобщение теоретического и практического материала изученной темы;

♦ изучение опыта и анализ состояния методики обучения;

♦ подбор, анализ и решение задач по данной теме.

Изучение теоремы Пифагора позволяет существенно расширить круг геометрических задач, решаемых школьниками, давая им в руки вместе с признаками равенства треугольников достаточно мощный аппарат решения задач.

Соответствующие умения являются опорными для решения вычислительных задач и доказательства ряда теорем в курсе планиметрии и стереометрии. Кроме того, они используются и в курсе физики.

В главе 1 внимание обращается на те или иные вопросы теоретического характера, такие как свойства прямоугольного треугольника, признаки равенства прямоугольных треугольников, теорема Пифагора, признаки подобия треугольников. Даны доказательства многих теорем.

В главе 2 представлены методические рекомендации для изучения данной темы, характеристика возрастных особенностей учеников 7- 8 классов, что позволяет учителю правильно строить уроки; разработаны некоторые примерные уроки по данной теме.

Практическая значимость работы заключается в том, что данный материал может быть использован студентами педагогических Вузов для работы на лабораторных занятиях по методике преподавания математики, а также работа будет интересна начинающим специалистам некоторыми своими методическими рекомендациями.

1. Теоретические вопросы темы «пр"ямоугольный треугольник»

.1 Введение понятия прямоугольного треугольника

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки - сторонами.

На рисунке 1 мы видим треугольник с вершинами A, B, C и сторонами AB, AC, CB.

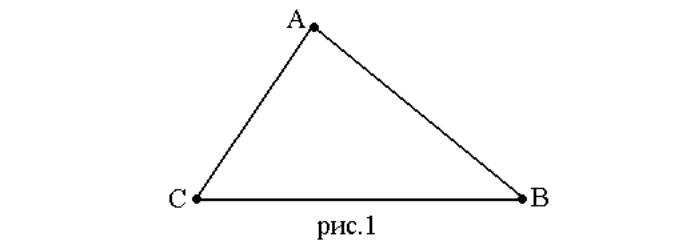
Треугольник обозначается указанием его вершин. Вместо слова «треугольник» иногда употребляют знак Δ. Например, треугольник на рисунке обозначается так: Δ ABC. Три угла-  BAC CBA, ACB - называют углами треугольника ABC. Часто их обозначают одной буквой A, B, C.

Треугольник называется прямоугольным, если у него есть прямой угол. Стороны прямоугольного треугольника имеют специальные названия:

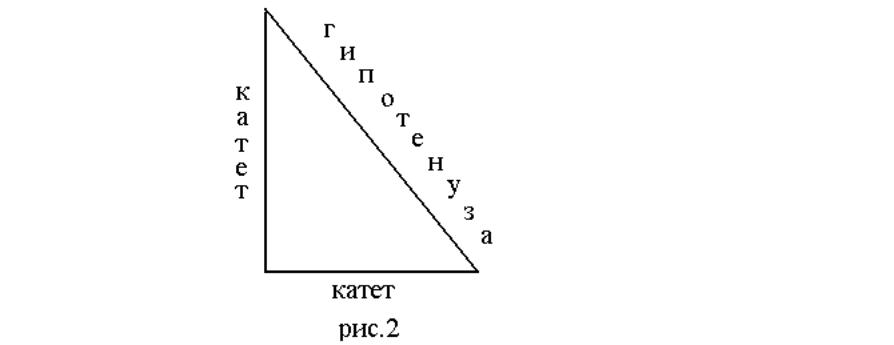
гипотенуза - сторона, лежащая против прямого угла; катеты - стороны прилежащие гипотенузе (рис. 2).

Так как сумма углов в треугольнике равна 180˚, то у прямоугольного треугольника только один прямой угол. Два другие угла прямоугольного треугольника - острые. Сумма острых углов в прямоугольном треугольнике равна 180º - 90º = 90º.

УТВЕРЖДЕНИЕ. В прямоугольном треугольнике гипотенуза больше катета.

В самом деле, гипотенуза лежит против прямого угла, а катет, против острого. Так как прямой угол больше острого, то гипотенуза больше катета.

1.2 Прямоугольный треугольник и его свойства

Рассмотрим свойства прямоугольных треугольников, которые устанавливаются с помощью теоремы о сумме углов треугольника.

В прямоугольном треугольнике гипотенуза больше катета (следствие из теоремы о соотношении между сторонами и углами в треугольнике).

1°. Сумма двух острых углов прямоугольного треугольника равна 90°.

В самом деле, сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника равна 90°.

2°. Катет прямоугольного треугольника, лежащего против угла в 30º, равен половине гипотенузы.

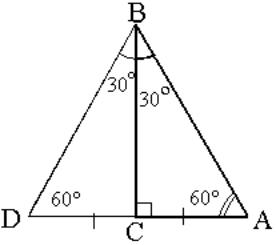
Пусть ABC - прямоугольный треугольник с прямым углом C и углом B равным 30º, а значит, угол A равен 60° (рис. 3). Построим треугольник DBC равный треугольнику ABC, как показано на рисунке. У треугольника ABD все углы равны (60º), поэтому он равносторонний.

Так как AC=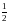 AD, а AD=AB, то AC= AB.

Что и требовалось доказать.

3°. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30º (обратная теорема).

Рассмотрим прямоугольный треугольник ABC, у которого катет AC равен половине гипотенузы AC (рис. 4 а). Докажем, что <ABC = 30°.

Приложим к треугольнику ABC равный ему треугольник DBC так, как показано на рисунке 4 б). Получим равносторонний треугольник DBA. Углы равностороннего треугольника равны друг другу, поэтому каждый из них равен 60°. В частности < DBA=60°. Но <DBA=2<ABC. Следовательно, <ABC=30°.

Что и требовалось доказать.

1.3 Признаки равенства прямоугольных треугольников

Чтобы установить равенство прямоугольных треугольников, достаточно знать, что два элемента одного треугольника соответственно равны двум элементам другого треугольника (исключая прямой угол). Это, конечно, не распространяется на равенство двух углов одного треугольника двум углам другого треугольника.

Так как в прямоугольном треугольнике угол между двумя катетами прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует:

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны (рис 5).

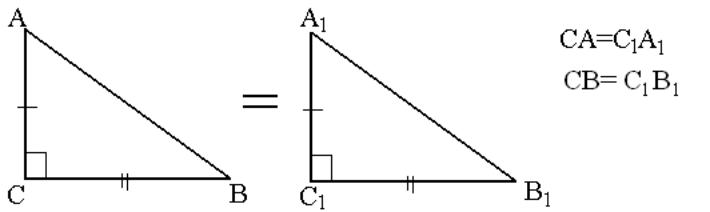
Далее, из второго признака равенства треугольников следует:

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему углу другого треугольника, то такие треугольники равны (рис. 6).

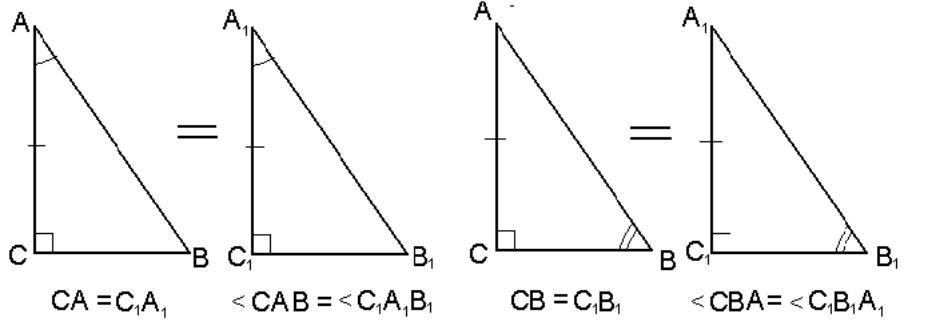
Рассмотрим ещё два признака равенства прямоугольных треугольников.

ТЕОРЕМА. Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого треугольника, то такие треугольники равны (рис. 7).

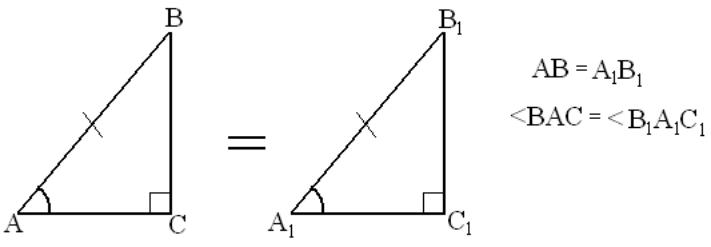
ДОКАЗАТЕЛЬСТВО. Из свойства 1º § следует, что в таких треугольниках два других острых угла тоже равны, поэтому треугольники равны по второму признаку равенства треугольников, то есть по стороне (гипотенузе) и двум прилежащим углам.

Что и требовалось доказать.

ТЕОРЕМА. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.

ДОКАЗАТЕЛЬСТВО. Рассмотрим треугольники ABC и A₁B₁C₁, у которых углы C и C₁ - прямые, AB =A₁B₁, BC = B₁C₁ (рис. 8).

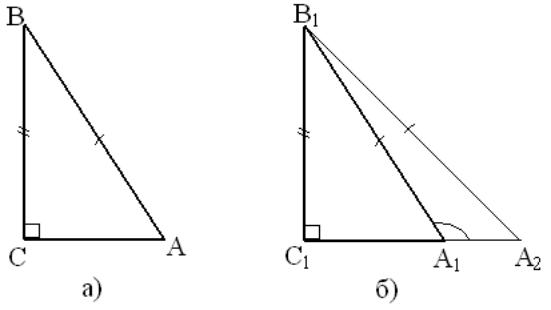
Так как < C = < C₁, то треугольник ABC можно наложить на треугольник A₁B₁C₁ так, что вершина C совместится с вершиной C₁, а стороны CA и CB наложатся соответственно на лучи C₁A₁ и C₁B₁, поскольку CB = C₁B₁, то вершина B совместится с вершиной B₁. Но тогда вершины A и A₁ также совместятся. В самом деле, если предположить, что точка A совместится с некоторой другой точкой A₂ луча C₁A₁, то получим равнобедренный треугольник A₁B₁A₂, в котором углы при основании A₁A₂ не равны (на рисунке < A₂ - острый, а < A₁ - тупой как смежный с острым углом B₁A₁C₁). Но это невозможно, поэтому вершины A и A₁ совместятся. Следовательно, полностью совместятся треугольники ABC A₁B₁C₁, то есть они равны.

Что и требовалось доказать.