6.2. Выборка из двумерной генеральной совокупности

Системой случайных величин (СВ) называют совокупность СВ, характеризующих состояние рассматриваемой системы или исход данного опыта.

Обозначение:

– n-мерная СВ.

Каждую из величин называют составляющей или компонентой.

Различают дискретные и непрерывные многомерные СВ: дискретные – если составляющие этих величин дискретны, и непрерывные – когда составляющие этих величин непрерывны.

Полной характеристикой ССВ является ее закон распределения, который может иметь разные формы: функция распределения, плотность распределения, таблица вероятностей отдельных значений случайного вектора и т.д.

Рассмотрим двумерную СВ , возможные значения которой – пары чисел .

Закон распределения дискретной двумерной СВ может быть задан таблицей распределения (матрицей распределения) (таблица 3), элемент которой, стоящий на пересечении i-той строки и j-того столбца, равен вероятности того, что двумерная случайная величина имеет значение :

.

Таблица 3

			…		…
			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

События при образуют полную группу, поэтому сумма всех вероятностей равна единице:

.

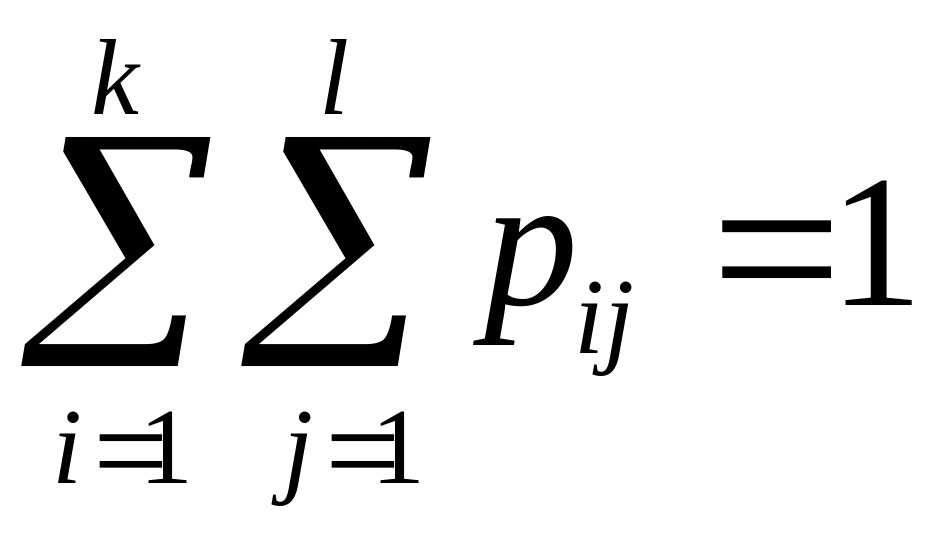Зная матрицу распределения двумерной ДСВ можно найти законы распределения каждой из составляющих. Чтобы найти вероятность того, что одномерная случайная величина Х или Y примет значение или , следует сложить все вероятности , стоящие в строке с номером i или столбце с номером j.

Две случайные величины Х и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое возможное значение приняла другая случайная величина. В противном случае величины Х и Y называются зависимыми.

При изучении двумерных случайных величин рассматриваются числовые характеристики одномерных составляющих Х и Y - математические ожидания и дисперсии: . Также рассматриваются условные математические ожидания и условные дисперсии. Например, условным математическим ожиданием одной из случайных величин, входящих в систему , называется ее математическое ожидание, вычисленное при условии, что другая случайная величина приняла определенное значение.

Условное математическое ожидание случайной величины Y при заданном , т.е. функция

,

называется функцией регрессии случайной величины Y относительно случайной величины Х (у на х). График этой функции называется линией регрессии у на х.

Аналогично определяется функция регрессии х на у,

Числовые характеристики системы не исчерпываются числовыми характеристиками случайных величин, входящих в систему. Может иметь место взаимная связь между случайными величинами, составляющими систему. Для ее описания вводят в рассмотрение числовую характеристику – корреляционный момент.

Корреляционным моментом (или ковариацией) случайных величин Х и Y называется математическое ожидание произведения отклонения этих величин от своих математических ожиданий:

.

Эта характеристика помимо рассеяния величин Х и Y описывает еще и связь между ними. Если случайные величины Х и Y независимы друг от друга, то корреляционный момент равен нулю. Обратное утверждение неверно, т.е. из равенства нулю корреляционного момента не следует независимость случайных величин Х и Y.

Формула для вычисления корреляционного момента дискретных случайных величин:

.

Для характеристики связи между величинами Х и Y в чистом виде переходят от момента к безразмерной характеристике - коэффициенту корреляции случайных величин Х и Y:

,

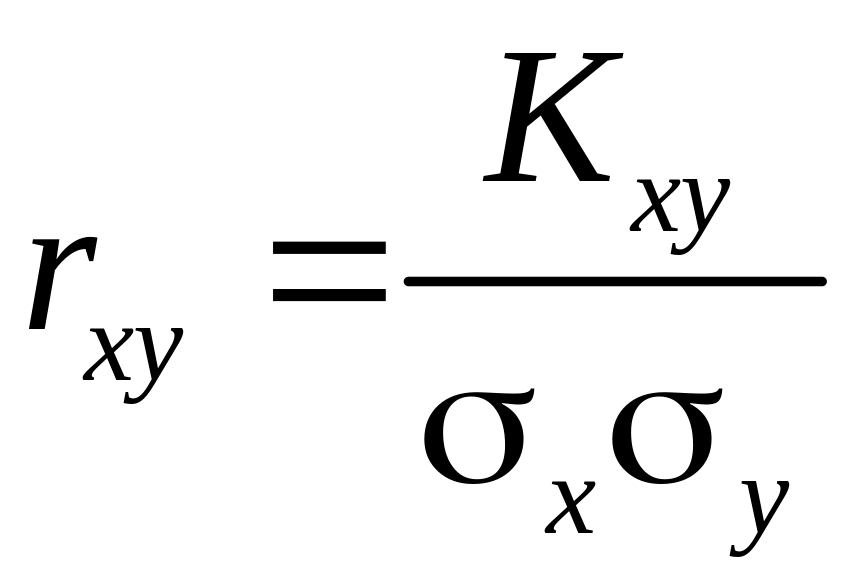где и – средние квадратические отклонения величин Х и Y.

Коэффициент корреляции принимает значения на отрезке :

.

Если случайные величины Х и Y независимы, то их коэффициент корреляции равен нулю.

Случайные величины, для которых корреляционный момент, а значит и коэффициент корреляции, равен нулю, называется некоррелированными (несвязанными).

Две независимые случайные величины всегда являются некоррелированными. Обратное утверждение не всегда верно, могут быть случаи, когда случайные величины являются некоррелированными, но зависимыми.

Если , где n – число двумерных случайных величин, то связь между случайными величинами Х и Y достаточно вероятна.

Рассмотрим выборку из двумерной генеральной совокупности, отождествляемой с системой двух случайных величин . В результате n независимых наблюдений получили n пар чисел:

.

Статистический материал сводят в корреляционную таблицу (таблица 4):

Таблица 4

			…		…
			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…
							n

где - частоты наблюденных пар значений признаков , , n – объем выборки.

Если по данным корреляционной таблицы построить законы распределения для каждой компоненты X и Y, то числовые характеристики выборки можно найти по формулам:

выборочные средние значения компонент

, ;

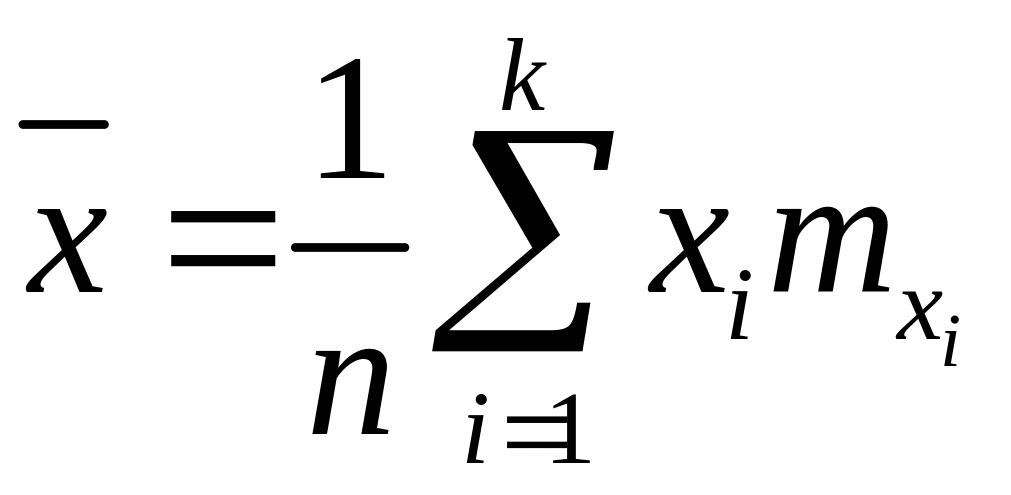выборочные дисперсии компонент

,

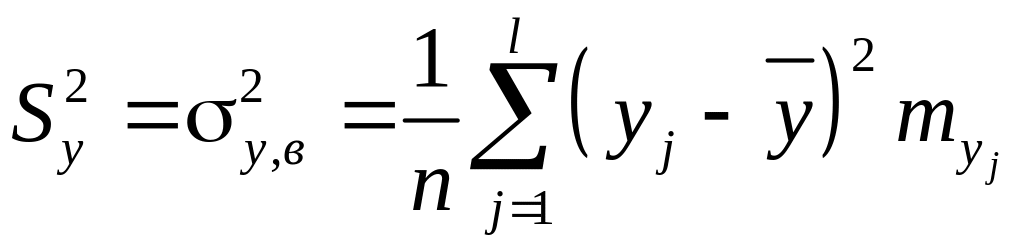
или

, ;

выборочный корреляционный момент

или

;

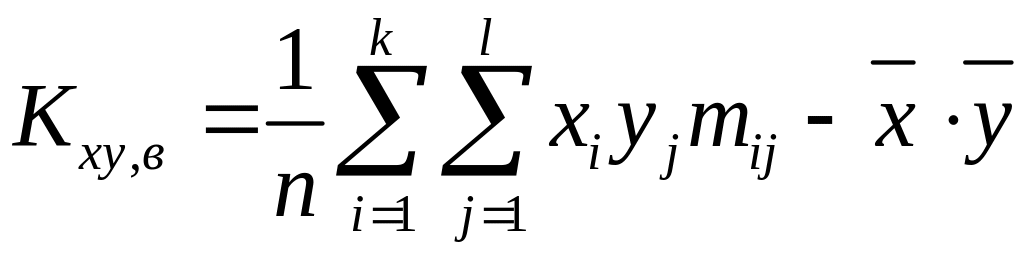выборочный коэффициент корреляции

;

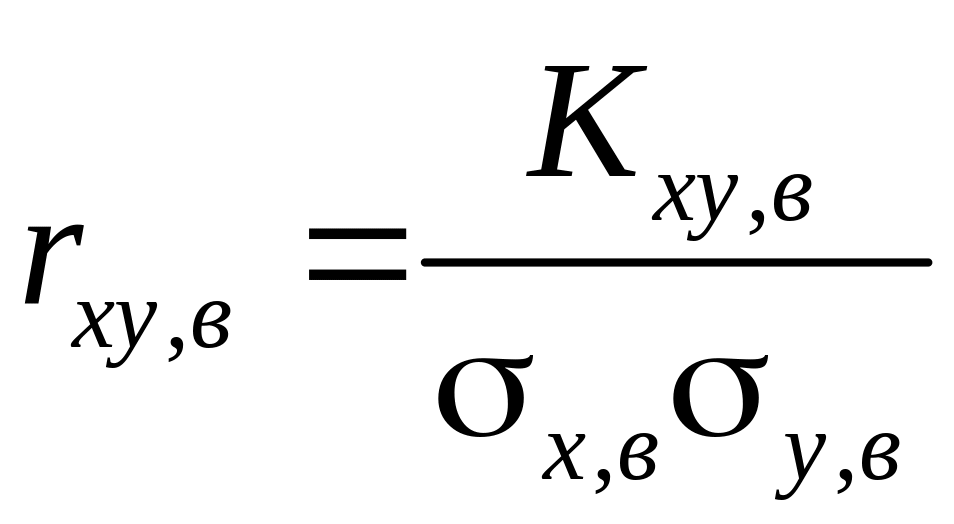условные средние компонент

, ,

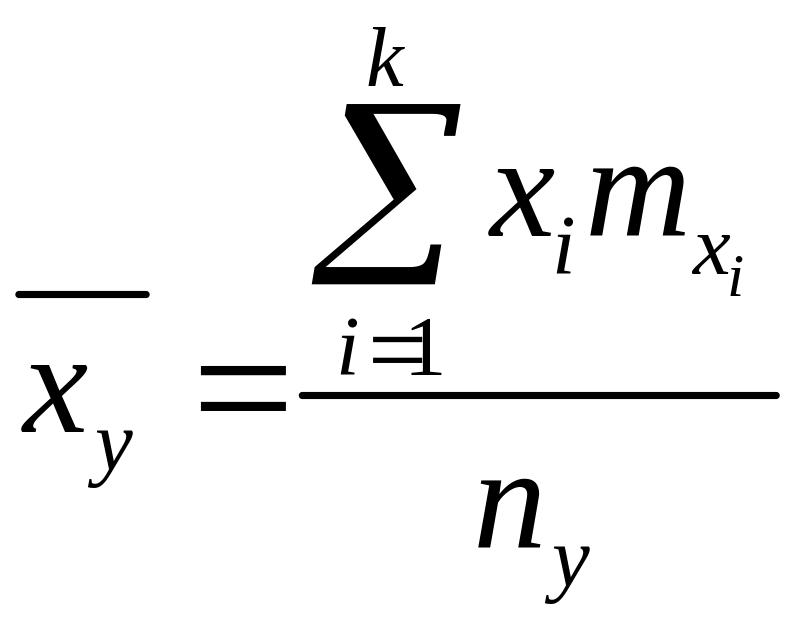где усреднение ведется в 1-ой формуле лишь по тем , которые появились совместно с данным у, а во 2-ой формуле лишь по тем , которые появились совместно с данным х.

Функция регрессии имеет важное значение при статистическом анализе зависимостей и может быть использована для прогнозирования значений одной из СВ, если известны значения другой СВ. Точность такого прогноза определяется условной дисперсией. Однако возможности практического применения функции регрессии весьма ограничены, так как для ее использования необходимо знать аналитический вид двумерного распределения . Поэтому идут на упрощение и вместо корреляционной зависимости рассматривают статистическую зависимость, которая устанавливает функциональную связь между значениями одной из величин и условным средним другой величины, например

,

эта функция называется эмпирической функцией регрессии, а ее график – эмпирической линией (кривой) регрессии. На практике получают лишь оценку кривой регрессии, так как число значений величины Х в выборке конечно.

Функция регрессии обладает замечательным свойством – она дает наименьшую среднюю погрешность оценки прогноза, т.е. величина

является минимальной именно для функции

.

На этом свойстве построен метод наименьших квадратов для определения неизвестных параметров функции регрессии.

Сущность метода наименьших квадратов состоит в выборе линии регрессии таким образом, чтобы сумма квадратов отклонений экспериментальных значений Y от теоретических была наименьшей.

Для иллюстрации метода рассмотрим частный случай линейной регрессии

.

По данным выборки требуется определить параметры а и b.

Строим функцию :

.

Используя корреляционную таблицу функцию можно записать в виде

.

Составляем необходимые условия экстремума:

.

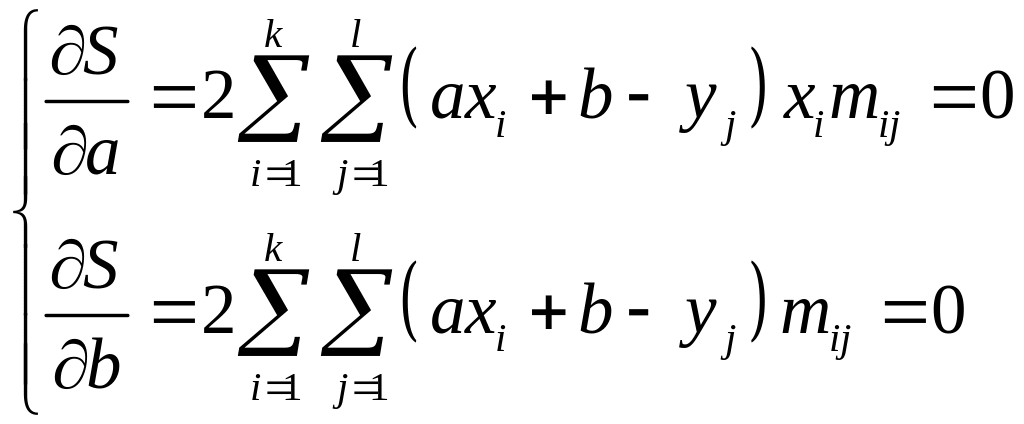После упрощения система примет вид:

.

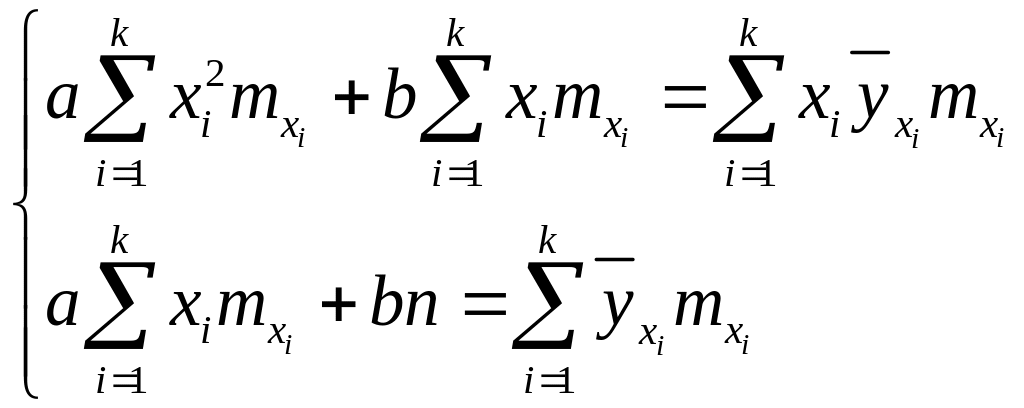Последнюю систему называют нормальной, решая ее получаем значения неизвестных коэффициентов а и b.

Уравнение регрессии можно также найти путем вычисления коэффициента регрессии. Уравнение регрессии у на х можно записать в виде

.

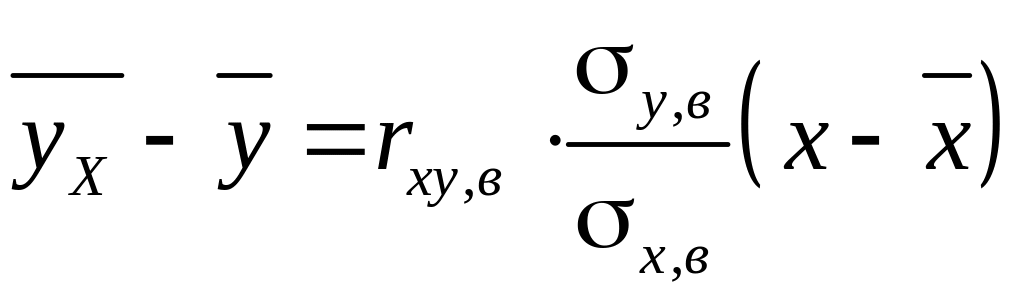Число 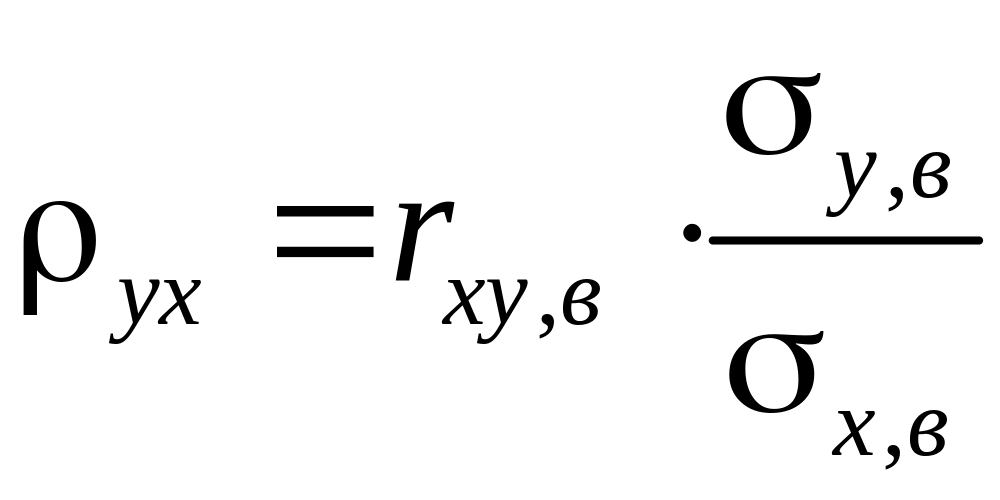называют коэффициентом регрессии у на х.

Пример

Двумерная выборка результатов совместных измерений признаков х и у объемом измерений задана корреляционной таблицей:

Таблица 5

Y X	3	4,2	5,4	6,6	7,8
1,2	2	3	–	–	–	5
3	3	8	2	–	–	13
4,8	–	14	18	–	–	32
6,6	–	–	10	8	–	18
8,4	–	–	9	10	–	19
10,2	–	–	3	6	1	10
12	–	–	–	1	2	3
	5	25	42	25	3	100

1. Найти выборочные средние и выборочные дисперсии .

2. Построить уравнение линии регрессии у на х в виде .

3. На графике изобразить корреляционное поле, т.е. нанести точки и построить прямую .

Решение

1. Запишем законы распределения для случайных величин Х и Y:

	1,2	3	4,8	6,6	8,4	10,2	12
	5	13	32	18	19	10	3

	3	4,2	5,4	6,6	7,8
	5	25	42	25	3

Найдем числовые характеристики. Выборочные средние:

,

,

,

;

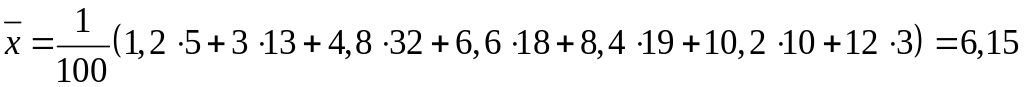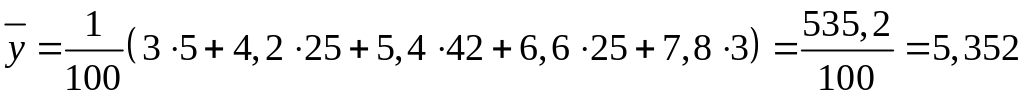выборочные дисперсии:

,

,

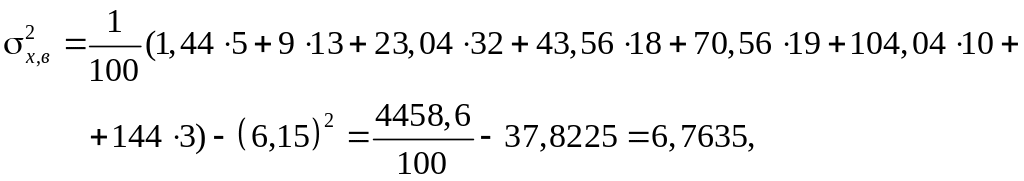
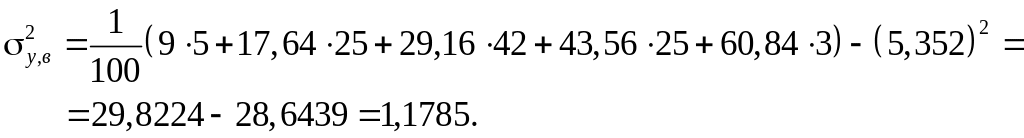
2. Найдем уравнение линии регрессии у на х по методу наименьших квадратов, для этого составим систему уравнений для нахождения коэффициентов а и b:

,

выше при вычислении числовых характеристик было найдено:

, .

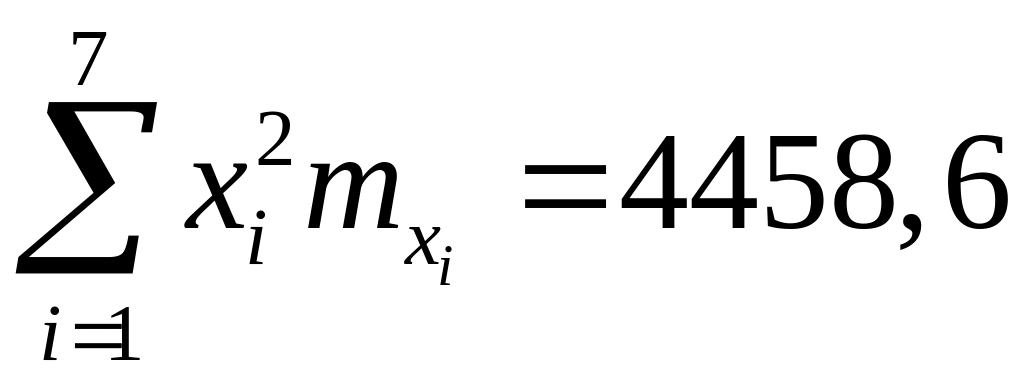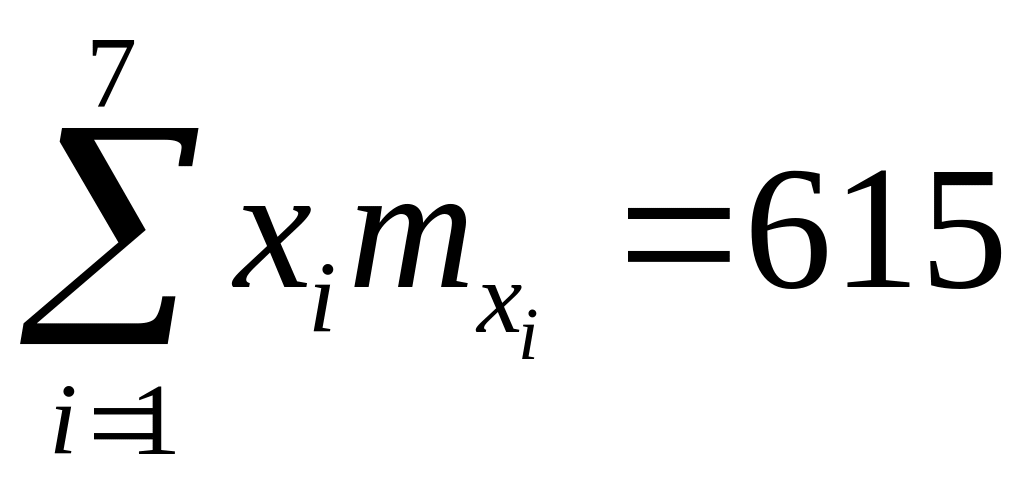Используя корреляционную таблицу каждому варианту признака Х поставим в соответствие среднее арифметическое соответствующих ему (входящих с ним в пару) значений признака Y, т.е.

,

результаты вычислений сведем в таблицу (таблица 6).

Таблица 6

	1,2	3	4,8	6,6	8,4	10,2	12
	3,72	4,10769	4,875	5,9333	6,03157	6,36	7,4

Вычислим:

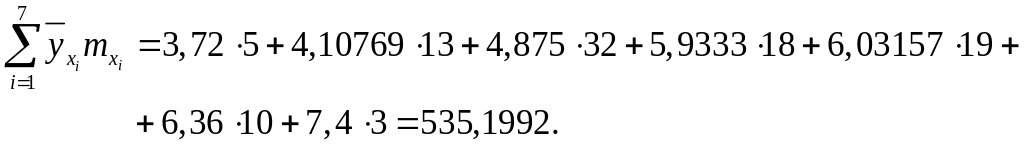
Подставим найденные коэффициенты и свободные члены в систему, получим

.

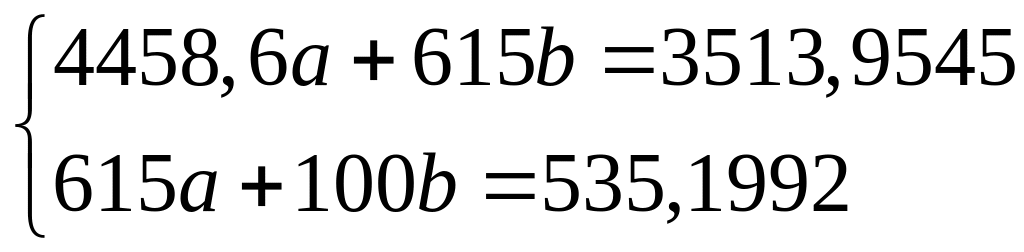Решим систему по формулам Крамера:

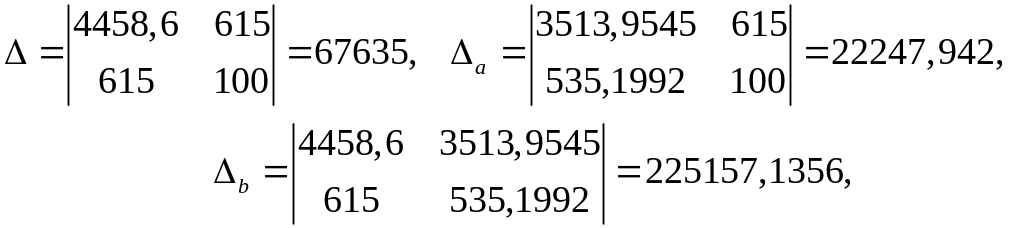
тогда

.

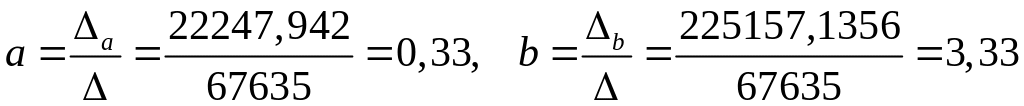Таким образом, эмпирическая функция регрессии у на х имеет вид:

.

Найдем ту же эмпирическую функцию регрессии у на х путем вычисления коэффициента регрессии

.

Найдем:

, ,

выборочный корреляционный момент найдем по формуле

,

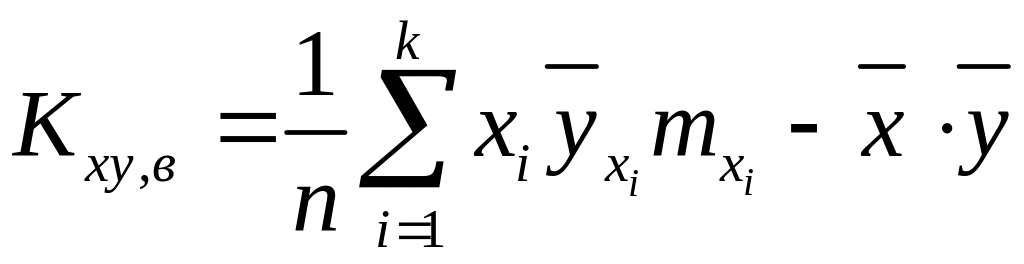в нашем случае

,

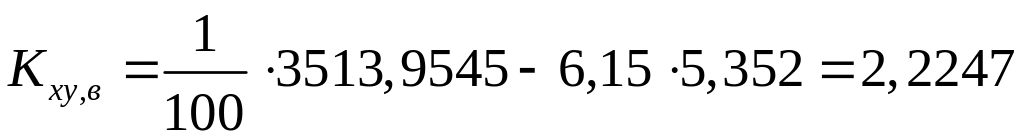выборочный коэффициент корреляции найдем по формуле

,

в нашем случае

.

Проверим гипотезу о существования связи между факторами Х и Y, вычислим :

,

следовательно, связь достаточно вероятна.

Подставим найденные значения в уравнение

,

получим

,

после преобразований получаем уравнение эмпирической функции регрессии у на х

.

3. Изобразим корреляционное поле и построим прямую (рис. 3).

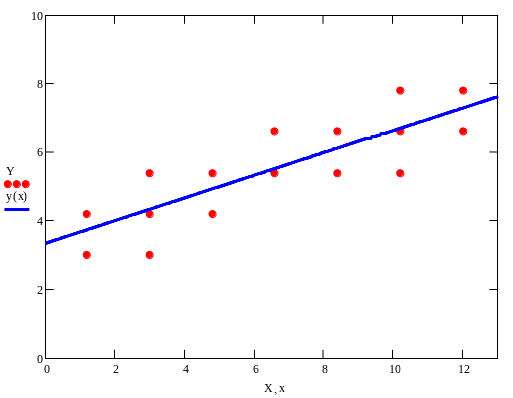
Рис. 3

Краткое содержание (программа) курса