5.2. Формула полной вероятности

Пусть имеется n попарно несовместных и единственно возможных событий H_i, i=1,2,…,n и пусть событие А может осуществиться в результате реализации одного из событий H_i, которые называют гипотезами.

Пусть вероятности Р(Н_i) наступления случайных событий H_i известны и известны условные вероятности Р(А/Н_i) случайного события А по каждому из событий Н_i .

Требуется найти вероятность Р(А) случайного события А, которая называется полной вероятностью события А, она определяется по формуле

.

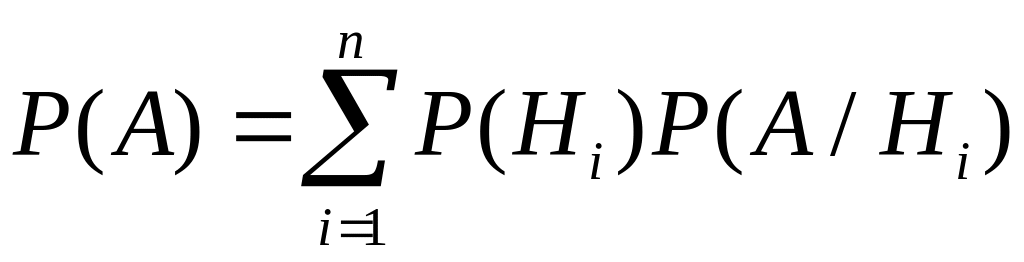Следует обратить внимание на то, что 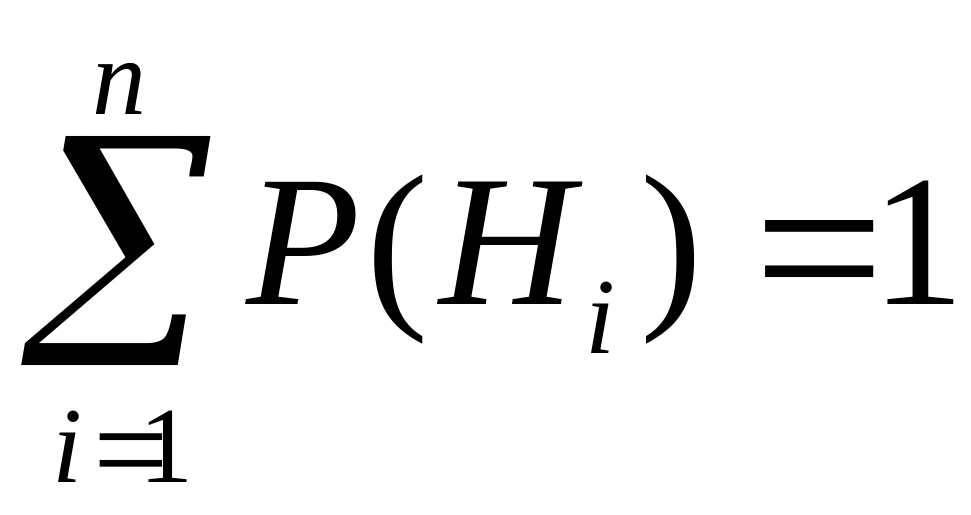, так как гипотезы образуют полную группу событий.

Пример

Имеются две коробки, в которых находятся по 8 красных карандашей и 4 синих и четыре коробки, в которых находятся по 5 красных карандашей и 7 синих. Наудачу выбирается коробка и из нее наудачу извлекают карандаш. Найти вероятность того, что вынутый карандаш красный.

Решение

Событие А – вынут красный карандаш.

Возможны следующие гипотезы:

– выбрана коробка, в которой 8 красных и 4 синих карандаша,

– выбрана коробка, в которой 5 красных и 7 синих карандашей.

Вероятности гипотез равны: .

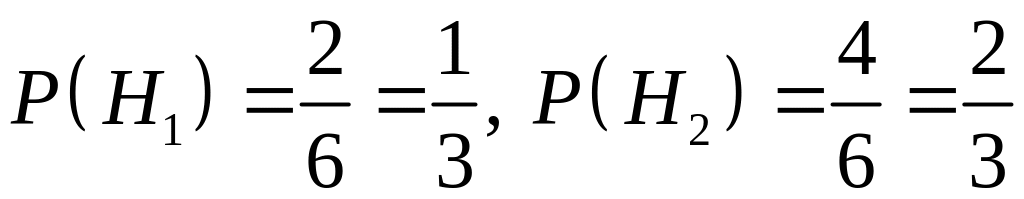Условные вероятности события А при этих гипотезах равны: , .

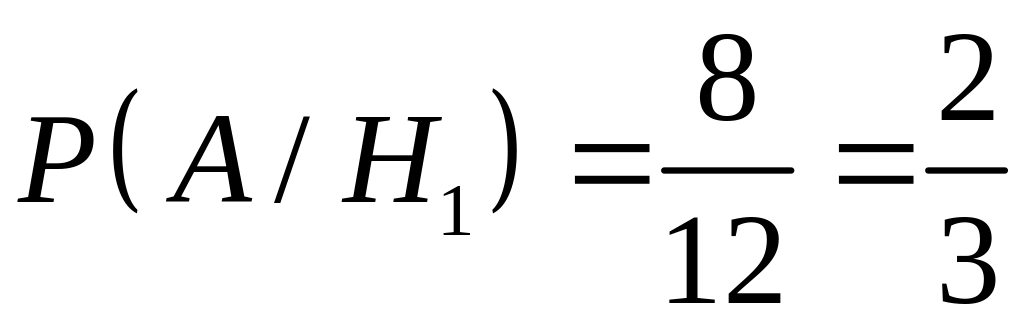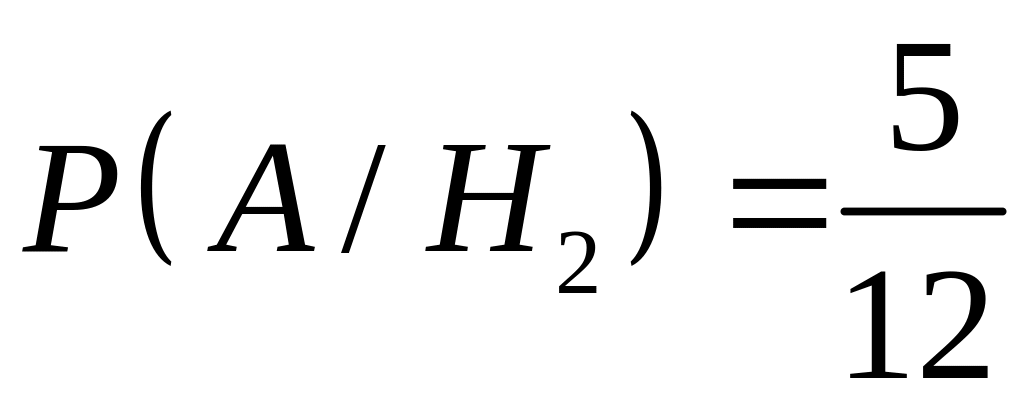По формуле полной вероятности

.

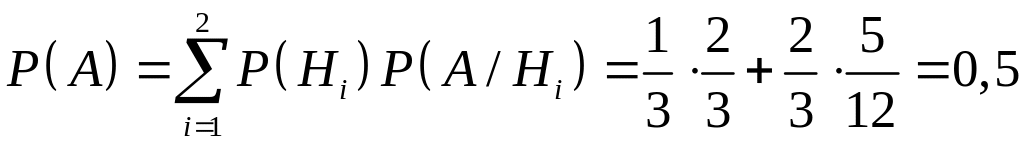5.3. Формула Бернулли и ее следствия

Пусть проводится n последовательных независимых одинаковых испытаний (экспериментов), в каждом из которых событие А может появиться с одной и той же вероятностью p и не появиться с вероятностью . Вероятность появления события в каждом опыте не зависит от того, появилось или нет это событие в других экспериментах (т.к. испытания независимые).

Вероятность того, что в n независимых испытаниях событие А появится ровно m раз , выражается формулой Бернулли

, где .

Из формулы Бернулли вытекает ряд важных следствий, широко используемых на практике, в частности, при контроле качества изделий, в теории стрельбы, в теории связи и т.д.

Следствия формулы Бернулли

1. Вероятность того, что в серии из n опытов событие А появится хотя бы один раз вычисляется по формуле: .

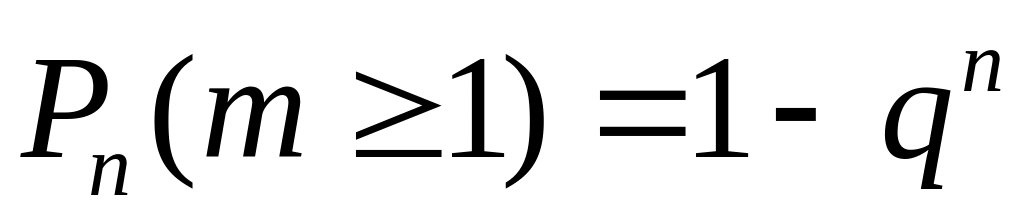2. Вероятность того, что в серии из n опытов событие А появится не менее k раз (k и больше) находится по формуле: .

3. Вероятность того, что в серии из n опытов событие А появится не более k раз (k и меньше) находится по формуле: .

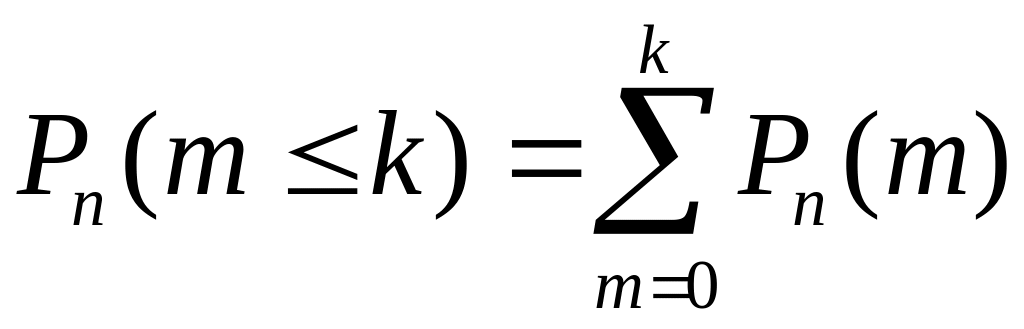4. Число опытов необходимых для того, чтобы событие А появилось хотя бы один раз с вероятностью не менее заданной Р находится по формуле: , где Р – заданная вероятность, р – вероятность появления события А в каждом опыте.

5. Число наступлений события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз. Наивероятнейшее число наступлений события А в n испытаниях заключено между числами np-q и np+p .

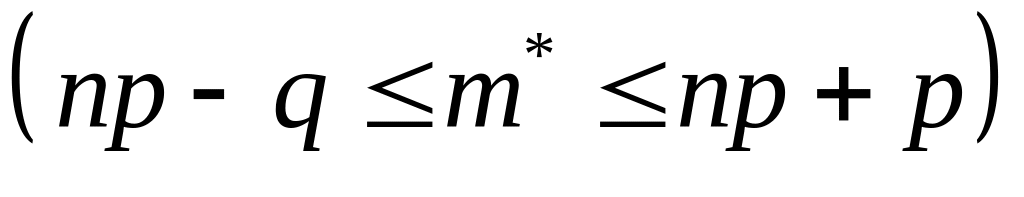Пример 1

Вероятность попадания в мишень при одном выстреле для данного стрелка 0,7 и не зависит от номера выстрела. Найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.

Решение

Поскольку , то . По условию , , по формуле Бернулли получим

.

Пример 2

Для нормальной работы автобазы на линии должно быть не менее восьми машин, а имеется их десять. Вероятность невыхода каждой машины на линию равна 0,1. Найти вероятность нормальной работы автобазы на ближайший день.

Решение

Автобаза будет работать нормально (событие D), если на линию выйдет или восемь (событие А), или девять (событие В), или все десять (событие С) автомашин.

По теореме сложения вероятностей

.

Каждое слагаемое найдем по формуле Бернулли. Поскольку вероятность невыхода каждой автомашины на линию равна 0,1, то вероятность выхода автомашины на линию будет равна 0,9, т.е. . Из условия следует, что . Следовательно,

.

Пример 3

Вероятность попадания в мишень при одном выстреле равна 0,8. Найти наиболее вероятное число попаданий в мишень при 5 выстрелах и соответствующую этому числу вероятность.

Решение

Воспользуемся неравенством

.

Поскольку , , то . Вероятность находим по формуле Бернулли:

.

Пример 4

Вероятность того, что наудачу взятая деталь нестандартная . Найти вероятность того, что среди 5 деталей будет не более двух нестандартных (событие А).

Решение

Искомую вероятность находим, используя следствие из формулы Бернулли:

.