Билет 9.
1.
.
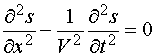(12.8)
Общее решение этого уравнения имеет вид
,
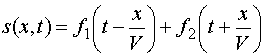(12.9)
где 
и 
–
произвольные функции, а аргументы этих
функций представляют собой специальные
комбинации переменных 
и
постоянной 
.
Смысл этих решений прост. Если в
момент 
графически
изобразить функции 
и 
,
то в последующие моменты времени эти
функции смещаются вдоль оси 
со
скоростью
как
целое:
–
вправо, а
–
влево.
Мы
ограничимся в дальнейшем, так называемыми,
гармоническими монохроматическими
волнами, т. е. синусоидальными волнами
с одной циклической частотой: 
.
Гармоническая
зависимость любой величины 
от
времени может быть представлена в общем
виде так:
,
где 
–
значение рассматриваемой величины в
точке с координатой
в
начальный момент времени: 
.
Решение волнового уравнения (12.8),
удовлетворяющее условию (12.9) и дающее
гармоническую зависимость
от 
,
имеет вид
.
(12.10)
Фаза
волны, т. е. ее состояние в данной точке
пространства в данный момент времени,
определяется выражением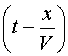 
.
В данный момент времени поверхность
равной фазы – волновой фронт – описывается
уравнением: 
.
Это плоскость, нормальная к оси
и
перпендикулярная направлению
распространения волны. Поверхность
равной фазы (волновой фронт) распространяется
вправо с фазовой скоростью
.
Поскольку
волновой фронт является плоскостью, мы
получили плоскую волну. Нам понадобится
еще выражение для плоской волны,
распространяющейся в произвольном
направлении, характеризуемом постоянным
единичным вектором 
.
Поскольку уравнение плоскости,
перпендикулярной вектору
,
имеет вид 
,
плоскую волну можно записать в виде
.
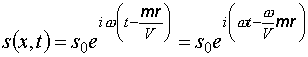(12.11)
Введем волновой
вектор 
,
определив его как
,
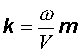(12.12)
где – единичный вектор в направлении распространения волны (в направлении ). Тогда плоская волна может быть представлена в виде
.
(12.13)
Вектор 
называют
волновым вектором потому, что он имеет
непосредственное отношение к длине
волны и всегда перпендикулярен фронту
волны. Длиной
волны,
как известно, называется расстояние
(отсчитанное в направлении движения
волны) между двумя ближайшими точками
волны, обладающими одинаковой фазой (в
данный момент времени). Рассмотрим
плоскую волну (12.11) и допустим, что фазы
в точках 
и 
одинаковы.
Тогда в любой момент времени должно
соблюдаться равенство
.
Это
может быть лишь в том случае, если 
,
т. е.
.
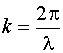2. Пространственная когерентность означает сильную корреляцию (фиксированную связь фаз) между электрическими полями в разных местах по всему профилю пучка. Например, в сечении пучка с лазерным дифракционным качеством, электрическое поле в разных местах колеблется фиксированным образом, даже если временная структура усложняется наложением различных частотных составляющих. Для пространственной когерентности необходимым условием является точная направленность лазерного луча.
• Временная когерентность означает сильную корреляцию между электрическими полями в одном месте, но в разное время. Например, на выходе одночастотный лазер может обладать очень высокой временной когерентностью, поскольку электрическое поле со временем развивается весьма предсказуемым образом: оно обладает чистым синусоидальным колебанием в течение длительного периода времени.
Лазеры могут излучать пучки света (например, гауссовые пучки) с очень высокой пространственной когерентностью, и это, пожалуй, самое принципиальное различие между лазерным излучением и излучением от других источников света. Высокая пространственная когерентность возникает из-за существования мод резонатора, которые определяют в пространстве коррелированные модели поля. В ситуациях, когда только одна мода резонатора имеет достаточное усиление для возникновения генерации, может быть выбрана только одна продольная мода для получения одночастотной генерации лазера, также с очень высокой временной когерентностью.