
- •Билет 1.
- •Билет 2.
- •Билет 3.
- •Билет 4.
- •Билет 5.
- •Билет 6.
- •Билет 7.
- •Билет 8.
- •Билет 9.
- •Билет 10.
- •Билет 11.
- •Билет 12.
- •Билет 13.
- •Билет 14.
- •Билет 15.
- •Билет 16.
- •Билет 17.
- •Билет 18.
- •Билет 19.
- •1. Введем вектор - приращение плотности электромагнитной энергии, где сама величина w определяется интегралом:
- •Билет 20.
- •Билет 21.
- •Билет 22.
- •Билет 23.
- •Билет 24.
- •Билет 25.
- •Билет26.
- •Билет 27.
- •Билет 28.
- •Билет 29.
- •Билет 30.
Билет 4.
для описания закономерностей поляризации света следят за поведением вектора
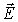 .Плоскость,
образованная векторами
и
.Плоскость,
образованная векторами
и 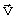 ,
называется плоскостью поляризации.Если
колебания вектора
происходят
в одной фиксированной плоскости, то
такой свет (луч) называется
линейно-поляризованным [cм. рис. 2 во
второй лекции]. Его условно обозначают
так
,
называется плоскостью поляризации.Если
колебания вектора
происходят
в одной фиксированной плоскости, то
такой свет (луч) называется
линейно-поляризованным [cм. рис. 2 во
второй лекции]. Его условно обозначают
так 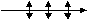 .
Если луч поляризован в перпендикулярной
плоскости (в плоскости хоz,
см. Рис. 2 во второй лекции), то его
обозначают
.
Если луч поляризован в перпендикулярной
плоскости (в плоскости хоz,
см. Рис. 2 во второй лекции), то его
обозначают  .Естественный
свет (от обычных источников, солнца),
состоит из волн, имеющих различные,
хаотически распределенные плоскости
поляризации (см. рис.3)Естественный свет
иногда условно обозначают так
.Естественный
свет (от обычных источников, солнца),
состоит из волн, имеющих различные,
хаотически распределенные плоскости
поляризации (см. рис.3)Естественный свет
иногда условно обозначают так 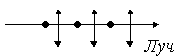 Его
называют также неполяризованным.
Его
называют также неполяризованным.
Интенсивность ![]() прошедшей
поляризатор
прошедшей
поляризатор ![]() волны,
пропорциональная, как неоднократно
указывалось выше, квадрату модуля
вектора напряжённости её электрического
поля, может быть определена следующим
образом:
волны,
пропорциональная, как неоднократно
указывалось выше, квадрату модуля
вектора напряжённости её электрического
поля, может быть определена следующим
образом:
|
(8.4b) |
где ![]() -
интенсивность линейно поляризованной
электромагнитной волны, направляемой
на поляризатор
.
-
интенсивность линейно поляризованной
электромагнитной волны, направляемой
на поляризатор
.
Это соотношение называют законом Малюса для поляризованного света.
2.



Билет 5.
1.
![]() Плотность
заряда σ связана с напряженностью поля
в конденсаторе формулой (1.22)
Плотность
заряда σ связана с напряженностью поля
в конденсаторе формулой (1.22)
σ = Е/ε0
В данном рассмотрении удобнее характеризовать электрическое поле не вектором напряженности Е, а вектором электрической индукции D. Согласно (1.64) для вакуума D = ε0Е, поэтому σ = D. Тогда из (4.6) получаем
jсм = ![]()
В общем случае электрическое поле является функцией координат и времени, поэтому в последнем выражении следует использовать символ частной производной по времени:
jсм = ![]() (4.7)
(4.7)
Таким образом, плотность тока смещения равна скорости изменения электрической индукции. Ток смещения, естественно, не переносит зарядов. Из всех физических свойств электрического тока Максвелл приписал току смещения лишь одно свойство – способность создавать в окружающем пространстве магнитное поле.
При анализе магнитных полей важное значение имеет закон полного тока, который в интегральной форме имеет вид:
![]()
(3.3)
и гласит о том, что линейный интеграл по замкнутому контуру l от напряженности магнитного поля равен полному току, протекающему сквозь сечение, ограниченное этим контуром.
Под полным током понимают алгебраическую сумму токов проводимости, переноса и смещения.
В дифференциальной форме закон полного тока можно записать следующим образом:
![]()
2. Дифракция в параллельных лучах была рассмотрена Фраунгофером в 1821-1822 гг. Для получения пучка параллельных лучей света, падающих на щель или отверстие, обычно пользуются небольшим источником света, который помещается в фокусе собирающей линзы Л.
|
Пусть параллельный пучок монохроматического света падает нормально на непрозрачный экран, в котором прорезана узкая щель ВС, имеющая постоянную ширину b и длину l>>b (см. рис.4,а). Оптическая разность хода между крайними лучами ВМ и CN, идущими от щели под углом j к оптической оси линзы OF0 D=CD=bsinj. Разобьем щель ВСна зоны Френеля, имеющие вид полос, параллельных ребру Вщели. Ширина каждой зоны выбирается (согласно методу зон Френеля) так, чтобы разность хода от краев этих зон была равна l/2. |
При интерференции света от каждой пары соседних зон амплитуда результирующих колебаний равна нулю, так как эти зоны вызывают колебания с одинаковыми амплитудами, но противоположными фазами.Всего на ширине щели уместится D:
l/2= bsinj/(l/2) зон. Если число зон четное, т.е.
bsinj/(l / 2)=± 2mили bsinj=± ml , m=1,2,3-, (8)
то наблюдается дифракционный минимум (темная полоса).
Если число зон нечетное, т.е.
bsinj/(l / 2)= ± (2m+1)или bsinj= ± (2m+1)![]() ,
m=1,2,3-, (9)
,
m=1,2,3-, (9)
то наблюдается дифракционный максимум (светлая полоса).
В направлении j=0 наблюдается самый интенсивный центральный максимум нулевого порядка.
Распределение интенсивности на экране, полученное вследствие дифракции (дифракционный спектр) приведено на рис.4,б. Расчеты показывают, что интенсивности в центральном и последующем максимумах относятся как 1:0,045:0,016:0,008:-, т.е. основная часть световой энергии сосредоточена в центральном максимуме.
Углы, под которыми наблюдаются максимумы всех порядков, начиная с первого, зависят от длины волны света l. Поэтому, если щель освещать немонохроматическим светом, то максимумы, соответствующие разным длинам волн, будут наблюдаться под разными углами и, следовательно, будут пространственно разделены на экране. Получим дифракционный спектр, в отличие от призматического спектра.
Геометрическая оптика является приближенным предельным случаем, в который переходит волновая оптика, когда длина световой волны стремится к нулю. ДИФРАКЦИЯ СВЕТА в широком смысле - проявление волновых свойств света в предельных условиях перехода от волновой оптики к геометрической.

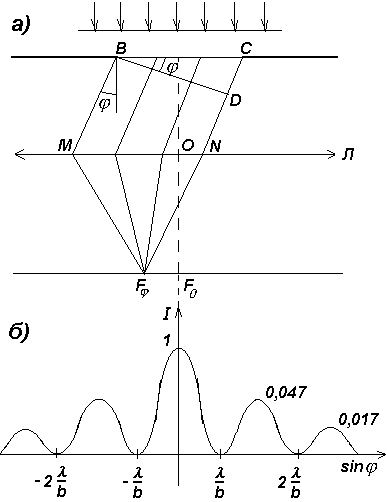 Рис.4
Рис.4