Задачи для самостоятельного решения
З
x
1
2
3
4
5
6
7
8
9
10
y
1,61
3,05
5,50
8,96
13,42
19,0
25,20
33,78
41,96
51,62
Предполагая,
что между переменными x
и y существует нелинейная
квадратичная зависимость, найти
эмпирическую формулу вида
,
используя метод наименьших квадратов.
Ответ:
искомая формула имеет вид
Задача 3.3. Индексы реального объема производства Y, реальных капитальных затрат K и реальных затрат труда L в промышленности страны за некоторый период времени приведены в таблице:
Год |
Y |
K |
L |
|
Год |
Y |
K |
L |
1 |
100 |
100 |
100 |
|
13 |
153 |
216 |
145 |
2 |
101 |
107 |
105 |
|
14 |
177 |
226 |
152 |
3 |
112 |
114 |
110 |
|
15 |
184 |
236 |
154 |
4 |
122 |
122 |
118 |
|
16 |
169 |
244 |
149 |
5 |
124 |
131 |
123 |
|
17 |
189 |
266 |
154 |
6 |
122 |
138 |
116 |
|
18 |
225 |
298 |
182 |
7 |
143 |
149 |
125 |
|
19 |
227 |
335 |
196 |
8 |
152 |
163 |
133 |
|
20 |
223 |
366 |
200 |
9 |
151 |
176 |
138 |
|
21 |
218 |
387 |
193 |
10 |
126 |
185 |
121 |
|
22 |
231 |
407 |
193 |
11 |
155 |
198 |
140 |
|
23 |
179 |
417 |
147 |
12 |
159 |
208 |
144 |
|
24 |
240 |
431 |
161 |
Используя метод
наименьших квадратов, определить
значения параметров А и
для функции Кобба-Дугласа вида
,
наиболее хорошо соответствующей
табличным данным. Выписать функцию с
найденными параметрами.
Ответ:
искомая функция имеет вид
.
Домашнее задание
Разобрать приведенный ниже материал. Прорешать задачи.
4.Задачи на оптимизацию параметров объектов и моделей
З
Марка
автомобиля
Значения ходовых
коэффициентов
Крейсерская
скорость,
км
/час
a
b
c
K
ГАЗ 31010
0,142
12
2000
0,0052
?
BMW
0,112
11
2100
0,0042
?
Volvo
0,121
10
2056
0,0047
?
Renault
0,115
11,1
1976
0,0051
?
Ford
0,108
12,1
1990
0,0048
?
Toyota
0,123
11,5
2001
0,0043
?
ВАЗ 2110
0,119
11,8
1992
0,0051
?
Cherokkie
0,121
10
1960
0,0045
?
бензина на 100 км пути, где v-скорость
автомобиля;
коэффициенты, зависящие от его ходовых
свойств. Найти наиболее экономичные
(крейсерские) скорости автомобилей
приведенных в таблице марок.
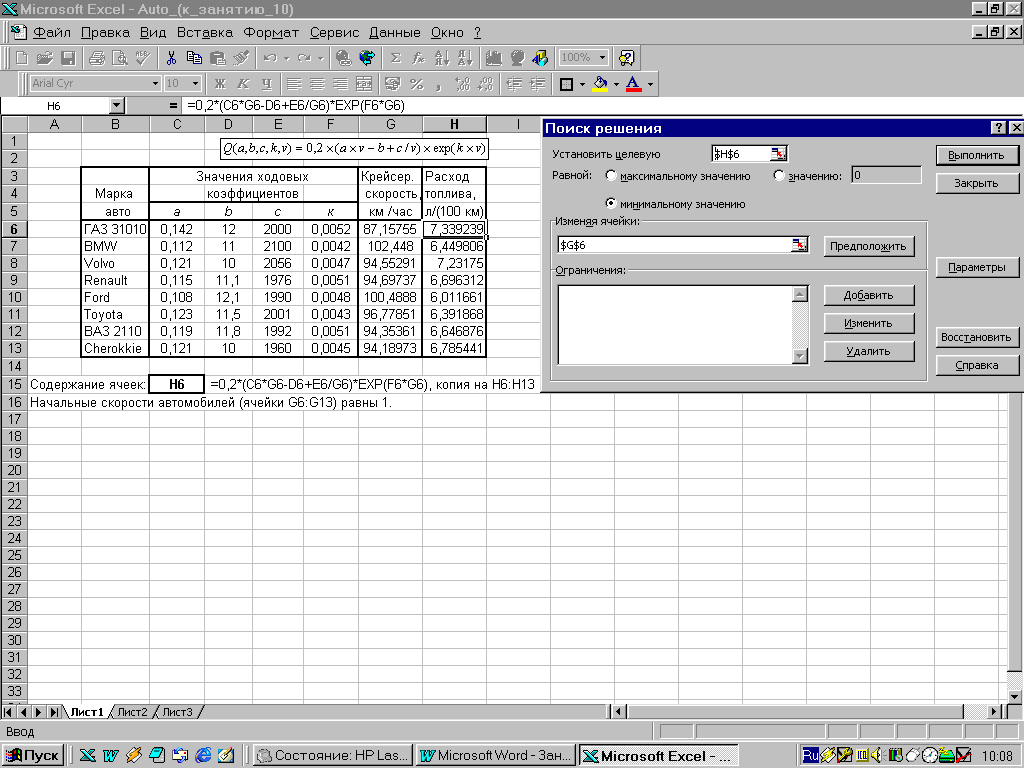
Для
решения задачи таблицу с данными копируем
в рабочий лист Excel; справа от столбца
"крейсерская скорость.." заносим
формулы, определяющие расходы топлива
,
а затем с использованием "Поиск
решения" проводим минимизацию этих
величин по скорости
.
Задача 4.2. На
строящейся станции метро длиной
м и высотой
м на осевой линии потолка должны быть
установлены три одинаковых мощных
светильника, один из которых расположен
в центральной части, а два других по обе
стороны от него на расстоянии
м. Освещенность станции метро на уровне
пола на уровне x м от
боковой стены вдоль его осевой линии с
учетом углов падения лучей выражается
формулой
,
где J =1000 лм – сила света одного светильника. Определить оптимальное расстояние yopt между светильниками, при котором освещение станции будет наиболее равномерно, то есть, при котором соотношение
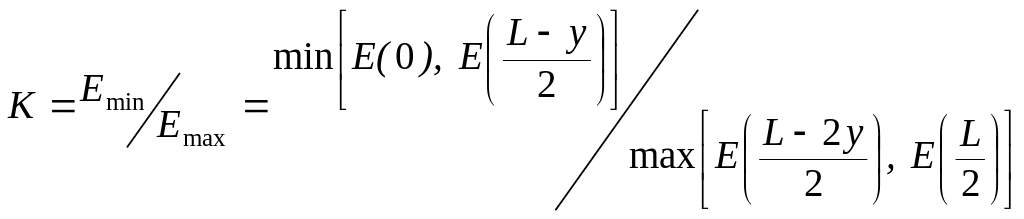
имеет наибольшее значение.
Ответ: yopt = 36,67 м.
Задача
4.3. Необходимо построить как
можно более короткий мост через морской
пролив. Берега пролива подчиняются
уравнениям
и
соответственно. Определить координаты
точек на берегах пролива, которые должны
быть соединены мостовым переходом и
его длину. Шириной мостового перехода
пренебречь.
Ответ: координаты точек имеют значения: (0,940; 0,938) на первом берегу и (0,062; 1,764) на втором. Длина перехода равна 1,205.
Задача 4.4. На
местности задана декартова система
координат. Две реки, текущие на
северо-восток, имеют бесконечно малую
ширину, но для переправы через эти реки
необходимо построить мосты. Реки текут
по прямым линиям, определяемым уравнениями
(первая река) и
(вторая
река).
Дорога в междуречье между мостами в любом случае будет проходить по прямой.
Координаты населенных пунктов заданы в таблицах. Населенные пункты (Л1-Л5) левобережья первой реки:
-
Л1
Л2
Л3
Л4
Л5
х
–13
–10
–2
–2
1
y
4
18
12
27
20
Населенные пункты (П1-П6) правобережья второй реки:
-
П1
П2
П3
П4
П5
П6
х
12
18
23
21
12
32
y
9
22
12
0
–6
7
Требуется определить координаты мостов через реки, для которых сумма расстояний от населенных пунктов левобережья первой реки до населенных пунктов правобережья второй реки принимает минимальное значение.
Ответ: мост на первой реке имеет координаты (3,048; 14,268);
мост на второй реке имеет координаты (7,011; 12,517).
Задача 4.5. Консервные банки, изготовляемые из жести, имеют цилиндрическую форму. Радиус основания цилиндра банки равен R см, высота банки – H см. Определить, при каких значениях R и H расход жести на изготовление консервных банок емкостью в 1 литр будет наименьшим.
Решение. Площадь
основания банки равна
площадь ее боковины
Общая площадь поверхности банки, таким
образом, равна
С другой стороны, вместимость (объем)
банки равен
,
следовательно,
,
и расход жести на изготовление банки
вместимостью V литров определится
выражением
.
Таким образом, решение задачи сводится
к решению следующей задачи нелинейного
программирования:
при ограничении
Ответ:
см,
см.
Задача 4.6. Стоимость С очищенной нефти, перевозимой морским путем из Ирака через Малаккский пролив в Японию (в долларах на килолитр), определяется в виде линейной суммы стоимости неочищенной нефти, затрат на страхование, таможенных тарифов, затрат на фрахт нефти, затрат на погрузку и разгрузку, платы за морскую стоянку судна, затрат, связанных с подводным перекачиванием и хранением, стоимости площади под цистернами, стоимости очистки и затрат на перевозку продуктов:
,
где
фиксированные
ежегодные расходы в относительных
величинах (0,20);
цена
неочищенной нефти, долл/кл (12,50);
страховка,
долл/кл (0,50);
таможенные
тарифы, долл/кл (0,90);
норма
процента (0,10);
число
портов (2);
цена
земли, долл/м2 (7000);
производительность
установки для очистки нефти, баррель/день;
объем
танкера, кл.
Считая значения, указанные в скобках, заданными, вычислите минимальную стоимость нефти и оптимальный объем танкера.
Ответ:
;
оптимальный объем танкера
кл
(
тыс.тонн).