2. Задачи оптимизации производственных процессов

Задача 2.1. Имеется фирма, производственная функция и функция полных издержек которой в зависимости от объема используемых факторов имеют соответственно вид

; ,

где параметры имеют следующие значения:

; ; ; .

Требуется определить размеры факторов , для которых при фиксированном уровне издержек в 190352 условных единиц достигается максимум производства продукции.

Решение. Необходимо решить задачу нелинейного программирования

Для ее решения создаем шаблон (рис. 2.1); начальные значения факторов полагаем равными единице.

Рис. 2.1. Шаблон с решением задачи 2.1

Задачи для самостоятельного решения

Задача 2.2. Производственная функция фирмы (производственная функция выражает объем выпускаемой фирмой продукции) имеет следующий вид:

,

где затраты ресурсов. Цена покупки фирмой единицы ресурсов равна 5 и 10 у.е. соответственно. Каков наибольший выпуск при общих издержках ?

Ответ: 66,66667 при 6,666667

Задача 2.3. Производственная функция фирмы имеет следующий вид:

,

где затраты ресурсов. Определить максимальный выпуск и обеспечивающие этот выпуск затраты ресурсов при условии, что . Каковы предельные продукты в оптимальной точке?

Ответ: 15 при .

Задача 2.4. Производственная функция фирмы описывается функцией Кобба-Дугласа:

,

где А=0,75 – технологический коэффициент, x– затраты капитала, y – суммарные затраты ресурсов. Найти значения величин x и y при ценах используемых ресурсов соответственно , чтобы при фиксированном объеме выпускаемой продукции обеспечивался минимум затрат , выражаемых формулой

.

При поиске решения принять ; .

Ответ: C_min=188561,8 при .

Задача 2.5. Достоверно установлено, что недельная прибыль фирмы определяется формулой

,

где затраты ресурсов первого и второго типов соответственно. Определить оптимальный расход ресурсов, при котором прибыль была бы максимальной, при условии, что себестоимости единицы ресурса первого и второго типов соответственно равны , а недельный бюджет фирмы, отведенный на суммарные затраты ресурсов определен в размере 15000.

Ответ: 100072,4 при 5,172414, 8,275862.

3. Задачи эконометрического типа, реализующие метод наименьших квадратов

Словесная формулировка. Имеется выборка наблюдений , где величины представляют собой заданные значения воздействий на некоторый объект, а величины являются откликами объекта на входные значения . Задача состоит в том, чтобы для фиксированной параметрической модели отклика определить оптимальные значения параметров, для которых сумма квадратов отклонений модельных значений откликов от их истинных значений была бы минимальна.

Формальная постановка:

. (3.1)

(3.2)

Задача 3.1. Имеются следующие данные о ценах на нефть x (ден. ед.) и соответствующих индексах акций нефтяных компаний y (усл.ед.):

x	17,28	17,05	18,30	18,80	19,20	18,50
y	537	534	550	555	560	552

Предполагая, что между переменными x и y существует линейная зависимость, найти эмпирическую формулу вида , используя метод наименьших квадратов.

Решение. В соответствии с (3.1)- (3.2) имеем задачу нелинейного программирования . Ограничений на значения параметров а и b нет.

Шаблон с решением представлен на рис. 3.1:

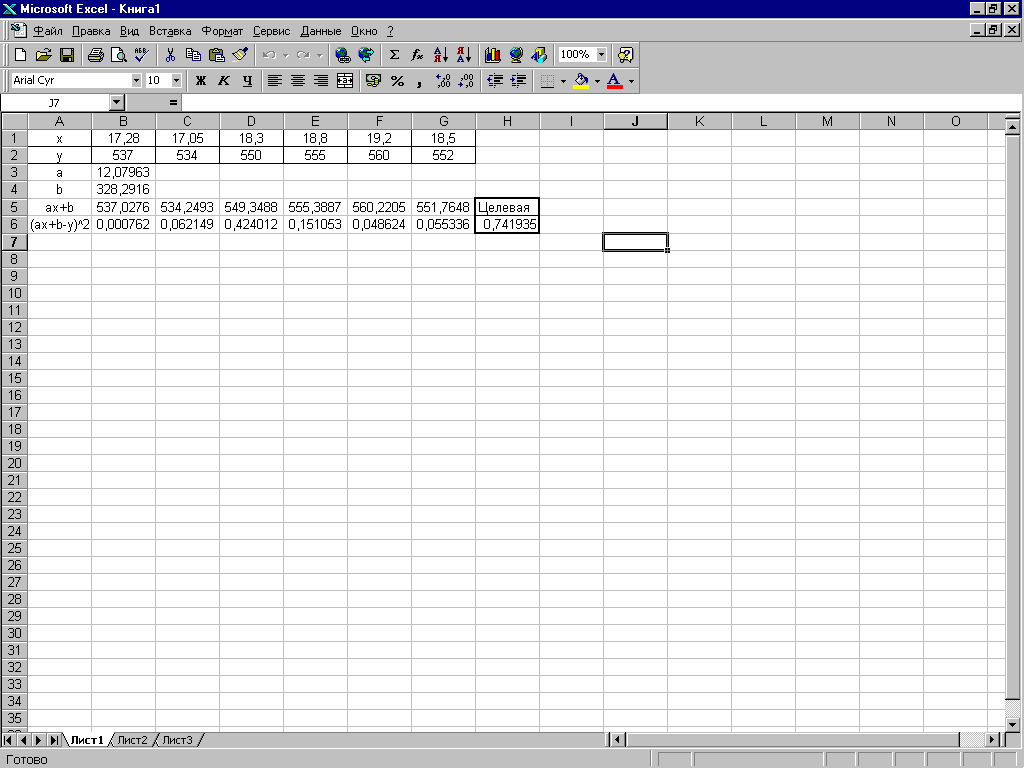
Рис. 3.1. Шаблон с решением задачи 3.1