Занятие 4 решение задач нелинейного программирования
Общая постановка задачи нелинейного программирования:
(
;
). (1)
Функция
в (1) называется целевой функцией, а
функции
и
- функциями ограничений. В общем
случае целевая функция и функции
ограничений могут быть нелинейными
функциями.
Задача 1 может быть решена средствами Excel с помощью встроенной процедуры «Поиск решения». Однако при этом очень внимательно следует выбирать точку начального приближения. Это обстоятельство особенно важно для так называемых мультимодальных функций, имеющих более одного экстремума.
1.Задачи оптимизации пространственного расположения объектов
Задача
1.1. На местности с заданной системой
координат OXY (ось ОХ
направлена на восток, а ось OY
– на север) протекает река в направлении
с юго-запада на северо-восток по прямой,
описываемой уравнением
.
По берегам реки находятся населенные
пункты A, B,
C, E, F,
G, H, координаты
расположения (км) которых приведены в
таблице:
-
A
B
C
D
E
F
G
H
x
30
7
–8
–25
–10
17
35
44
y
31
33
26
4
–14
–16
–14
17
На реке есть
водопад в точке с координатами
Пренебрегая шириной реки, определить место строительства моста, к расположению которого предъявляются следующие требования:
|
|
.
Решение.
Обозначим:
координаты
i-го населенного
пункта;
–
координаты водопада;
–
координаты моста. Тогда расстояние от
i-го населенного пункта
до моста равно
,
а расстояние от моста до водопада равно
.
Таким образом, решение задачи состоит
в определении координат моста
,
при которых суммарное расстояние R
от населенных пунктов до моста минимально
при условии, что мост расположен на реке
выше по течению от водопада и не ближе,
чем на 2,4 км от него:
;
Схема решения полученной задачи нелинейного программирования состоит в выполнении следующих шагов:
1) располагаем водопад и мост в одном ряду с населенными пунктами, вносим заданные координаты (рис.1.1 ниже);
2) вносим в игрековую координату моста формулу, описывающую протекание реки (ячейка K3 на шаблоне, рис.1.1);
5) вычисляем расстояния от населенных пунктов до моста и водопада (ячейки B4:J4 на шаблоне);
6) суммируем в отдельной целевой ячейке В6 расстояния от моста до населенных пунктов (водопад не трогаем!);
7) вызываем «Поиск решения», ставим задачу, линейную модель не отмечаем, жмем на «выполнить».
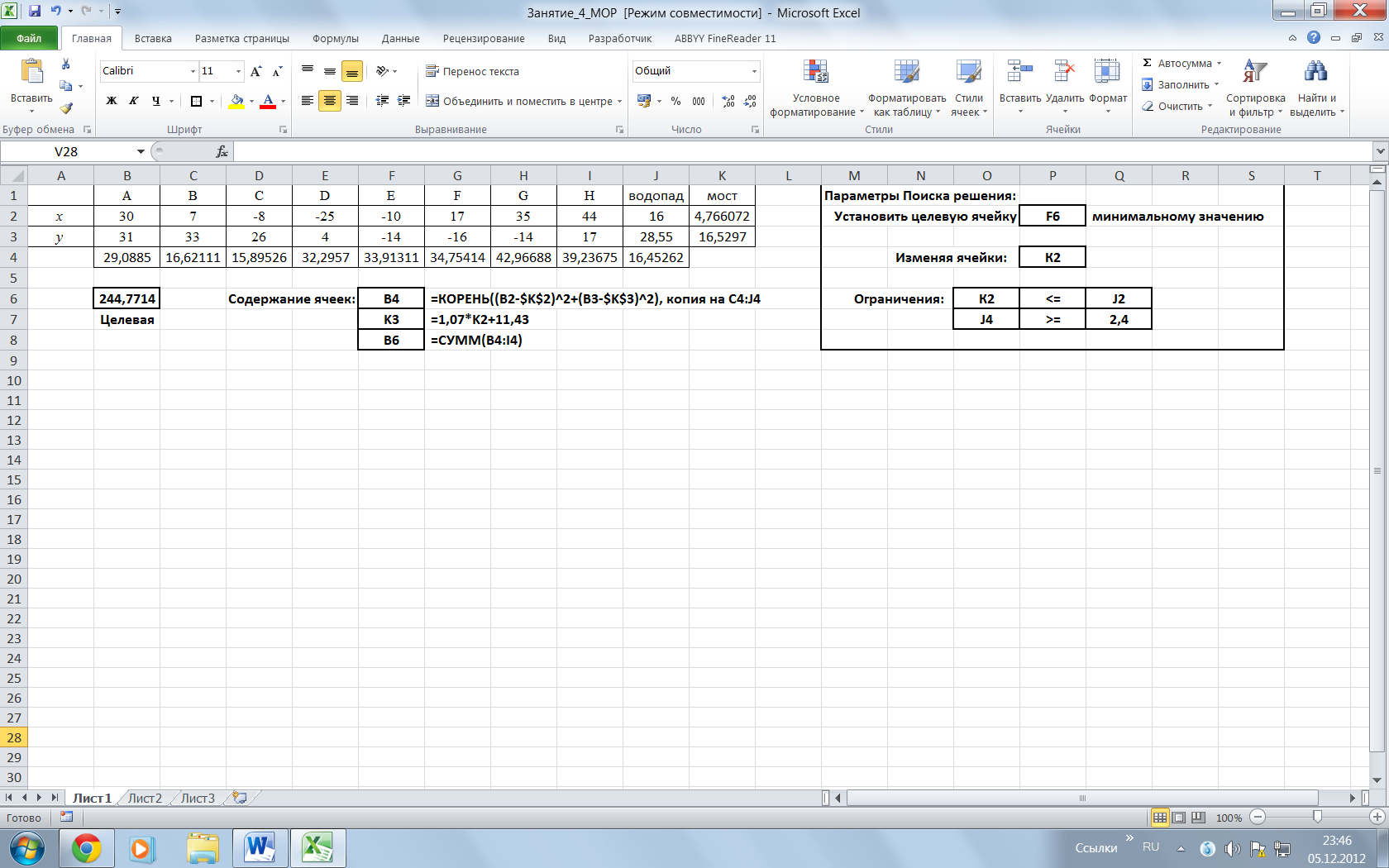
Рис.1.1. Шаблон с решением задачи 1.1