7) Решение произвольных систем линейных уравнений. Элементарные преобразования систем. Теорема Кронекера-Капелли. Метод Гаусса.
Рассмотрим систему m линейных уравнений с n неизвестными
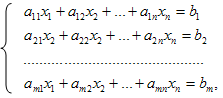i=1,…..,m;
j=1,…..,n,
(1)
Пусть
.
Разделим все члены первого уравнения
на
:
(2)
Где
(j
=1,2…n +
1),
(3)
Рассмотрим i-е уравнение системы(1):
(4)
Для
исключения из этого уравнения х1
умножим уравнение (2) на
и
полученное уравнение вычтем из уравнения
(4). Тогда будем иметь
(5)
где
(6)
Таким образом, получаем укороченную систему
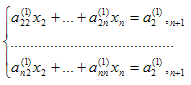(7)
коэффициенты которой определяют по формулам (6).
Если
ее ведущий коэффициент
,
то из системы (7) указанным выше приемом
можно исключить неизвестное х2,
причем новые коэффициенты будут
вычисляться по формулам типа (6) и т.д.
Эта часть вычислений называется прямым
ходом метода Гаусса.
Для определения неизвестных х1,х2,...хn рассмотрим уравнения
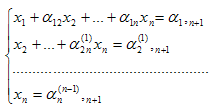(8)
Отсюда последовательно находим неизвестные (обратный ход):
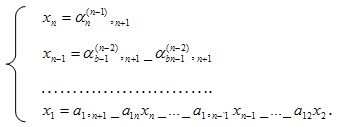(9)
Заметим, что операции (9) выполняются без деления. Если очередной ведущий коэффициент окажется равным нулю, то уравнения системы следует переставить надлежащим образом. Возможно, конечно, что система (1) несовместна. Тогда, естественно, метод Гаусса не допускает реализации.
_____________________________________________________________________
К элементарным преобразованиям системы линейных уравнений относятся:
1)Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю. 2)Перестановка уравнений местами. 3)Удаление из системы уравнений, являющихся тождествами для всех х. ___________________________________________________________________
Теорема Кронекера – Капелли
(условие совместности системы)(Леопольд Кронекер (1823-1891) немецкий математик) Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.