Трехкомпонентные системы.

На практике наряду с двухкомпонентными системами гораздо чаще приходится иметь дело с системами, составленными из трех и более компонентов. Уравнение состояния трехкомпонентных систем связывает между собой пять параметров и имеет следующий вид:

. (6.12) Из (6.12) следует, что диаграмма состояния трехкомпонентной системы не может быть изображена на плоскости. Полагая, что Р = const и С₁ + С₂ + С₃ = 1, если способ выражения состава сплавов мольные доли, трехкомпонентную диаграмму можно построить в трехмерном пространстве. Составы трехкомпонентных сплавов принято изображать на плоскости с помощью концентрационного треугольника. В вершинах треугольника располагаются чистые компоненты А, В и С, а три его стороны отражают составы двойных сплавов. Ось, перпендикулярная плоскости концентрационнго треугольника - температурная ось. Свойства концентрационного треугольника. Первое свойство. Если из какой-то точки М, лежащей в плоскости треугольника опустить три перпендикуляра на стороны, то:

М_А + М_В + М_С = const = BD, где BD - высота концентрационного треугольника (рис. 6.9, а).

Если BD принять за 100%, то каждый из перпендикуляров - концентрация каждого из компонентов в сплаве: Ма = % А; Мb = % B; Mc = % C. Второе свойство. Если через точку М, лежащей в плоскости треугольника, провести три параллельные сторонам треугольника прямые, то сумма отрезков Аb, Bc и Са, отсекаемых этими прямыми на сторонах треугольника - величина постоянная и равная стороне треугольника:

Аb + Вс + Са = const = АВ. Если АВ = % В, Вс = % С и Са = % А, то состав трехкомпонентного сплава определен. Таким образом, зная свойства равностороннего треугольника, по положению фигуративной точки можно оценить состав трехкомпонентного сплава или, зная его состав, можно найти положение фигуративной точки в плоскости концентрационного треугольника. Как и для двухкомпонентных систем, сложность диаграмм состояния трехкомпонентных систем зависит от взаимной растворимости компонентов и от возможности образования между ними химических соединений. Наиболее простой является диаграмма состояния трехкомпонентной системы с неограниченной растворимостью компонентов в жидком и твердом состояниях (рис. 6.10).

Д ля диаграммы на рис. 6.10 Т_S (B) > Т_S (A) > Т_S (С) т. А’, B’ и C’ - температуры плавления чистых компонентов. Грани призмы - двойные системы с неограниченной растворимостью компонентов в твердом и жидком состояниях. Через три ликвидуса проходит поверхность ликвидуса. Выше поверхности ликвидуса находится объем жидких растворов (L). Через три солидуса проходит поверхность солидуса. Ниже поверхности солидуса располагается объем твердых растворов (

). Объем пространства между поверхностями ликвидуса и солидуса занят равновесной двухфазной системой из жидких и твердых растворов (L + ). Интервал между поверхностью ликвидуса и солидуса - интервал кристаллизации (плавления) сплавов трехкомпонентной системы. Сплав состава т. М (рис. 6.10) при Т > Т₁ находится в состоянии ненасыщенного жидкого раствора. Кристаллизация сплава начинается при Т₁, лежащей на поверхности ликвидуса. Состав первых кристаллов - твердого раствора соответствует проекции точки 1’ на плоскость концентрационного треугольника. При дальнейшем понижении температуры от Т₁ до Т₂ жидкость постепенно принимает состав т. 2’ и исчезает, а кристаллы - твердого раствора - т. 2. Поэтому процесс кристаллизации сплава изображается уравнением вида: . (6.10) Ниже температуры Т₂ происходит охлаждение кристаллов твердого раствора . При работе с диаграммами состояния трехкомпонентных систем удобно пользоваться их разрезами - поли- и изотермическими. Изотермические разрезы характеризуют фазовые равновесия в тройных сплавах, а по политермическим разрезам устанавливают температуры начала и конца кристаллизации сплавов и т.д.

Растворение твердого вещества – происходит разрушение кристаллической решетки, это связано с затратой энергии. Одновременно с растворением происходит процесс сольватации (гидратации – когда в воде). Таким образом теплота складывается из двух слагаемых: (Qразрушения)+(Qсольватации)=Qраств. Знак теплового эффекта зависит от того, какой из слагаемых больше по абсолютной величине. Если вещество обладает относительно прочной кристаллической решеткой, то в процессе растворения, тепла для разрушения кристаллической решетки будет поглощаться больше, чем выделяться при сольватации. В результате чего раствор будет охлаждаться.

Теплоемкость.

Теплоемкость изменяется с изменением температуры, причем величина этого изменения различна в различных температурных интервалах. Качественно характер изменения С = f (Т) для большинства металлов, не испытывающих фазовых превращений в твердом состоянии представлен на рис. 2.1.

Рис. 2.1. Характер изменения теплоемкости с температурой.

Для металлов в твердом состоянии в области низких температур (T < T_комн.) характерна зависимость отвечающая уравнению кубической параболы: . С понижением температуры теплоемкость быстро уменьшается и при стремится принять нулевое значение. В области комнатных температур (Т_комн.) теплоемкость определяется из закона Дюлонга - Пти. Дальнейшее повышение температуры плавления (Т_S) вызывает непрерывное увеличение теплоемкости. Этот температурный участок представляет наибольший практический интерес. Для него зависимость С = f (Т) выражается с помощью эмпирических соотношений, имеющих вид степенных рядов:

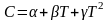, (2.18)

, (2.19) Теплоемкость для жидкого состояния (Т_S - T_E) характеризуется, как правило, меньшей величиной, чем для твердого состояния, причем не изменяющейся вплоть до температуры кипения (Т_Е).

Работа идеальных процессов.

Из определения функции "работа" следует, что она не является функцией состояния и ее величина зависит от того, в каких условиях она совершается. Изобарический процесс (p = const).

,

где , а .Тогда

, (1.17)

т. е. работа совершается при увеличении температуры системы. Изотермический процесс (Т = const).

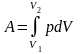, где , тогда

(1.18)Изобарно-изотермический процесс (Р, Т = const).

,

т. е. в системе с неизменным количеством вещества такой процесс невозможен. Если n₁ - количество вещества в системе до реакции, а n₂ - количество вещества в системе после реакции, то

, (1.19)

где - изменение количества вещества в системе за счет химической реакции. Адиабатический процесс. Адиабатический процесс характеризуется отсутствием энергообмена в форме теплоты с окружающей средой, что определяется математически в виде условия 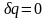. В этом случае уравнение первого начала принимает вид:

, (1.20) где . (1.21)

Тогда величина работы: , (1.21) где С_V - изохорическая теплоемкость системы, которая тем больше, чем сложнее устройство

молекул.

Рис. 1.1. Графическое изображение работы

расширения идеального газа от объема