Задание 1. Вычисление исходных дирекционных углов линий; решение прямой геодезической задачи

Задача 1. Вычислить дирекционные углы линий BC и CD, если известны дирекционный угол α_AB линии AB и измеренные по правому ходу углы β₁ и β₂ (рис.1).

Исходный дирекционный угол берется в соответствии с вариантом.

Пример.

α_AB = 45° 34,2′

Правый угол при точке B (между сторонами AB и CD)

β₁ = 189° 59,2′ для всех

правый угол при точке С (между сторонами BC и CD) вариантов

β₂ = 159° 28,0′

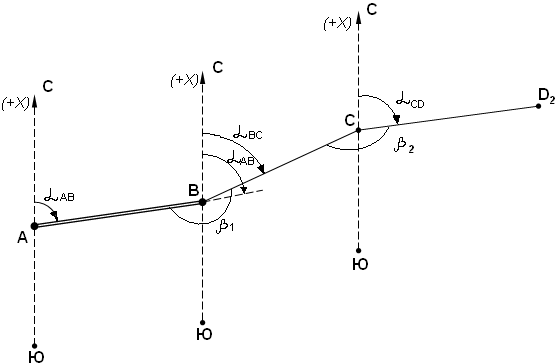
Рис. 1. Теодолитный ход.

Дирекционные углы вычисляются по правилу: дирекционный угол последующей стороны равен дирекционному углу плюс 180° и минус

Горизонтальный угол, справа лежащий. Следовательно,

α_BС = α_AB + 180° - β₁; α_CD = α_BC + 180° - β₂.

Пример. Вычисление дирекционных углов выполняем столбиком:

α_{AB ………. +} 45° 34,2′

180°

_- 225° 34,2′

189° 59,2′

α _{BС ………. +} 35° 35,0′

180°

_- 215° 35,0′

159° 28,0′

α_{CD ……….} 56° 07,0′

П р и м е ч а н и е. Если при вычислении уменьшаемое окажется меньше вычитаемого, то к уменьшаемому прибавляют 360°. Если дирекционный угол

получается больше 360°, то из него вычитают 360°.

Задача 2. Найти координаты x_С и y_С (рис.1), если известны координаты x_B и y_B точки B, длина (горизонтальное проложение) d_BC линии BC и дирекционный угол α_AB этой линии. Координаты точки В и длина d_BC берутся одинаковыми для всех вариантов: x_В = -14,02 м, y_В = +627,98 м, d_BC = 239,14 м. Дирекционный угол α_BС линии ВС следует взять из решения предыдущей задачи.

Координаты точки С вычисляются по формулам:

x_С = x_В + Δx_ВС; y_С = y_В + Δy_ВС ,

где Δx_ВС и Δy_ВС - приращения координат, вычисляемые из соотношений

Δx_ВС = d_BC cos α_BC ; Δy_ВС = d_BC sin α_{BС .}

Пример. Дано: d_BC = 239,14 м; α_AB = 35° 35′. Выполнив вычисления, получаем

Δx_ВС = +194,49 м; Δy_ВС = +139,14 м.

Координаты точки С получаем алгебраическим сложением координат точки В с приращениями по линии ВС, действуя по схеме:

₊ x_В - 14,02 ₊ y_В +627,98

Δx_ВС + 194,49 Δy_ВС +139,14

x_С + 180,47 y_С + 767, 12

Задачи решают в специальной тетради; решение каждой из них должно сопровождаться схематическим чертежом, соответствующим выполняемому варианту.

В задаче 1 пример подобран так, что вычисленный дирекционный угол α_CD последней линии должен получиться на 10° 32,8′ больше, чем исходный дирекционный угол α_AB. Это должно служить контролем правильности решения первой задачи.

Решение задачи 2 непосредственно не контролируется. К ее решению надо подойти особенно внимательно, так как вычисленные координаты x_С и y_С точки С будут использованы в следующем задании.