Модуль 2 теория потребительского поведения

Содержание модуля 2:

Тема 2.1 Сравнительный анализ существующих подходов к анализу полезности

Тема 2.2 Потребительский выбор и равновесие потребителя

Тема 2.3 Кривые «доход – потребление» и «цена – потребление»

Тема 2.1 Сравнительный анализ существующих подходов к анализу полезности

Анализ поведения потребителя основывается на следующих допущениях:

• поведение потребителя является рациональным, то есть он так распоряжается своим денежным доходом, чтобы извлечь из него как можно большее удовлетворение или полезность;

• потребитель имеет сложившуюся систему предпочтений в отношении товаров и услуг, предлагаемых на рынке;

• все товары и услуги, предлагаемые потребителям, имеют цену, отражающую фактор редкости.

Экономисты создали теорию потребительского поведения, основанную на гипотезе о сравнимости полезности разных благ. Предполагается, что при заданных ценах покупатель стремится так распределить свои средства на покупку различных благ, чтобы максимизировать ожидаемое удовлетворение своих потребностей или полезность от их потребления. При этом потребитель руководствуется своими личными вкусами и предпочтениями.

Предпочтение в экономике – это выбор благ, наборов благ экономическими субъектами из доступных альтернатив с учетом их значимости для потребителя. Основным преимуществом в экономике считается возможность получения выгоды (но не обязательно денежной). При этом выгодой для фирмы, как правило, выступает прибыль, а для потребителя – полезность благ. Полезность блага – это его способность удовлетворять потребность (или потребности) потребителей.

Очевидно, чтобы максимизировать ожидаемое удовлетворение потребностей или полезность приобретаемых благ, потребитель должен быть в состоянии каким-то образом сравнивать, сопоставлять, соизмерять полезности различных благ и их наборов, с учетом своих предпочтений. Известны два основных подхода к решению этой проблемы – количественный и порядковый.

Количественный поход в анализе полезности был предложен в последней трети XIX в. У. Джевонсом, К. Менгером, Л. Вальрасом одновременно и независимо друг от друга. Количественная (кардиналистская) теория полезности основана на представлении о возможности измерения полезности различных благ в гипотетических единицах– ютилах. В рамках данного подхода возможно построить функций полезности для наборов товаров.

Следует подчеркнуть, что количественные оценки полезности товара или товарного набора имеют исключительно индивидуальный, субъективный характер. Количественный подход не предполагает объективное измерение полезности того или иного товара в ютилах и не предусматривает также возможности соизмерения степени удовлетворения потребностей различными потребителями. Один и тот же продукт может представлять большую ценность для одного потребителя и никакой ценности – для другого.

Таким образом, согласно количественной теории полезности потребитель формирует свои индивидуальные предпочтения на то или иное благо в зависимости от данной им количественной оценки в ютилах полезности потребляемого им блага или набора благ.

Набор, в котором имеется только одно благо, представляется следующим образом: ( ), где - количество блага в наборе. Набор, состоящий их двух благ - ( ), где и , соответственно, количество одного и другого блага в наборе. В общем случае в наборе содержится товаров – . Зависимость между количеством блага или нескольких благ в наборе (независимой или независимыми переменными) и величиной их общей полезности ( - total utility) представляют функцией общей полезности, которая в зависимости от числа благ в наборе имеет вид:

.

Функция полезности — это такой способ приписывания каждому возможному потребительскому набору некоего численного значения, при котором более предпочитаемым наборам приписываются большие численные значения, чем менее предпочитаемым. Иными словами, набор предпочитается набору в том и только в том случае, если полезность набора больше полезности набора : на языке условных обозначений , если и только если . Единственный смысл приписывания полезности состоит в том, что с его помощью ранжируются товарные наборы.

Функция общей полезности непрерывна и дифференцируема. Это означает, что любое бесконечно малое изменение количества блага в наборе вызывает изменение общей полезности набора.

Допустим, что объемы потребления товаров постоянны. Как изменится общая полезность товарного набора при изменении объема потребления товара ? Графически эта зависимость отражена на рисунке 2.1 (а).

Длина отрезка равна полезности товарного набора при фиксированных объемах товаров в наборе и при нулевом объеме потребления товара . Функция общей полезности такого набора вначале возрастает (чем больше единиц блага в наборе, тем большую полезность он имеет); достигает своего максимума в точке S; после которой становится убывающей. Последнее означает, что после насыщения благом, каждая его дополнительная единица будет приносить потребителю меньшую общую полезность, чем предыдущая. Кривая общей полезности имеет выпуклую вверх форму: каждая последующая единица одного и того же блага увеличивает общую полезность на меньшую величину, чем предыдущая.

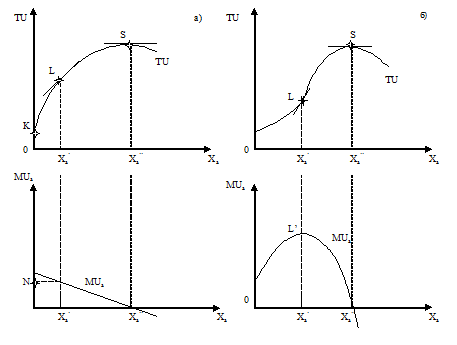
Рисунок 2.1 – Соотношение общей и предельной полезности

0

В процессе непрерывного потребления полезность каждой дополнительной единицы блага, его предельная полезность, убывает. Предельная полезность ( - marginal utility)- это прирост общей полезности товарного набора при увеличении объема потребления данного товара на одну единицу. На рисунке 2.1(а) представлена зависимость предельной полезности блага от объема его потребления.

Представим математическую интерпретацию предельной полезности. Общая полезность набора, состоящего из одного товара, . Если в наборе количество товара изменилось на величину , то полезность набора изменилась на :

.

Отношение приращения полезности к вызвавшему его приращению блага измеряет предельную полезность на дуге . Для бесконечно малого приращения аргумента (блага в наборе) определяют предельную полезность блага в точке, т.е. предельную полезность конкретной единицы блага. Для этого находим

.

Математически предельная полезность товара измеряется первой простой производная функции общей полезности товарного набора по объему потребления товара . Функция предельной полезности . График кривой предельной полезности представлен на рисунке 2.1.

Наклон кривой предельной полезности измеряется второй производной функции полезности: .

Если в наборе товаров , то общая полезность . Тогда предельная полезность товара измеряется следующим пределом: , т.е. частной производной функции общей полезности.

- измеряет наклон поверхности безразличия, описываемого аналитически функцией предельной полезности . Если , то .

Если в наборе товаров, то такой набор отмечается точкой в мерном пространстве, имеющей координат (по числу товаров в наборе) находящемся в пространстве товаров. Здесь наборы представлены точками на поверхности безразличия, касательной к которой является плоскость.

Графически значение предельной полезности равно длине отрезка (на нижнем рисунке) или тангенсу угла, который образует касательная к кривой в точке с положительно направленной осью абсцисс. Поскольку линия выпукла вверх, то с увеличением объема потребления -го товара наклон касательной уменьшается и, следовательно, предельная полезность товара понижается. Если при объеме потребления товара , общая полезность достигает максимума, то предельная полезность товара становится равной нулю.

Принцип убывающей предельной полезности называют первым законом Госсена, по имени немецкого экономиста Г. Госсена (1810-1859), впервые сформулировавшего его в 1854 г. Принцип убывающей предельной полезности заключается в том, что с ростом потребления какого-то одного блага (при неизменном объеме потребления всех остальных) общая полезность, получаемая потребителем, возрастает, но возрастает убывающим темпом. Математически это означает, что первая производная функции общей полезности по количеству данного блага положительна, а вторая – отрицательна:

, .

Однако принцип убывающей предельной полезности отнюдь не универсален. Во многих случаях предельная полезность последующих единиц благ сначала увеличивается, достигает максимума и после начинает снижаться. Такая зависимость характерна для небольших порций делимых благ. Она показана на рисунке 2.1(б). В интервале от нуля до общая полезность растает быстрее объема потребления блага, растет и предельная полезность. В интервале от до общая полезность растет медленнее объема потребления, а предельная полезность снижается от максимального значения (в точке ) до нуля. Математически это означает, что на участке от нуля до и первая и вторая частные производные функции общей полезности по объему данного блага положительны:

, .)

Таким образом, принцип убывающей полезности, или первый закон Госсена, справедлив лишь в том случае, если вторая частная производная функции общей полезности отрицательна. Однако поскольку потребитель покупает на рынке определенные блага, можем считать, что для обращающихся на рынке товаров первый закон Госсена выполняется.

Предельные величины - один из основных параметров современной микроэкономики. Анализ конкуренции, рыночных эффектов и парадоксов опирается на изучение потребностей и предпочтений человека, а также законов их насыщения и реализации.

Постепенно экономисты пришли к выводу, что применительно к потребительскому выбору полезность важна только в определении, обладает ли один набор благ более высокой полезностью, чем другой, а насколько более высокой — значения на самом деле не имеет. Это стало основой для развития альтернативной порядковой (ординалистской) теории полезности, представителями которой являются Ф. Эджуорт, В. Парето, И. Фишер, а в 30-х гг. 20 века после работ Р. Аллена и Дж. Хикса эта теория на западе стала общепринятой. Ординалистская теория полезности основана на следующих аксиомах:

1. Аксиома полной (совершенной) упорядоченности, или сравнимости. Допускаем, что любые два набора можно сравнить между собой. Если даны набор и набор , то либо , либо , либо имеет место то и другое одновременно. Последнее означает, что потребителю безразлично, какой из двух наборов потреблять.

2. Аксиома рефлексивности. Любой набор по крайней мере не хуже себя самого: .

3. Аксиома транзитивности. Если и , то . Иными словами, если потребитель считает, что набор по крайней мере не хуже набора , а набор по крайней мере не хуже набора , то, значит, он считает, что набор по крайней мере не хуже набора . Из этой аксиомы следует важное свойство кривых безразличия, которое гласит, что кривые безразличия никогда не пересекаются.

Графически удобно описать предпочтения, используя кривые безразличия. На рисунке 2.1 на осях координат отложено потребление неким потребителем товаров и . Выберем определенный потребительский набор и заштрихуем область всех потребительских наборов, предпочитаемых набору . Эта область называется слабо предпочитаемым множеством. Наборы, лежащие на границе этого множества, столь же хороши для данного потребителя, как и набор , образуют кривую безразличия.

Можно провести кривую безразличия через любой потребительский набор. На кривой безразличия все товарные наборы имеют для потребителя одинаковую полезность.

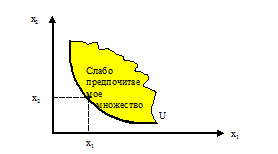
Рисунок 2.2 – Выражение предпочтения с помощью кривой безразличия

Одна из проблем использования кривых безразличия для описания предпочтений состоит в том, что точки на кривых показывают наборы, которые потребитель воспринимает как имеющие одинаковую полезность, и не отмечают при этом, какие наборы лучше, а какие хуже.

Кривую безразличия обычно обозначают буквой или , поскольку на ней представлено множество наборов одинаково предпочтительных для потребителя, т.е. множество наборов, имеющих одинаковую полезность для потребителя.

Для описания поведения потребителей с помощью типичных кривых безразличия, рассматриваемых в теории потребительского выбора, были введены еще три аксиомы в отношении предпочтений.

4. Аксиома ненасыщения. Если набор содержит не меньше каждого товара, а одного из них больше, чем набор , то . Смысл аксиомы в том, что она выражает желание потребителя иметь больше, по крайней мере, хотя бы одного товара. Для потребителя, чем больше содержится блага в наборе, тем лучше. Набор, лежащей на кривой безразличия более удаленной от начала координат, обладает большей полезностью, а, следовательно, предпочтительнее для потребителя (рис. 2.3а и 2.3б).

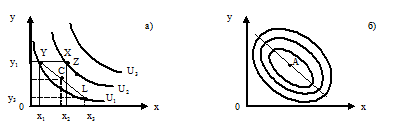
Рисунок 2.3 – Карта кривых безразличия

Данная аксиома предполагает, что потребность в благах, входящих в сравнимые наборы на определенном локальном отрезке времени, не получила удовлетворения. Иными словами, товары, входящие в набор, рассматриваются как благо для потребителя. Хотя по достижении определенной точки насыщения благом может стать не товар, а его отсутствие. Но в экономической теории анализируют отрезки кривых безразличия, расположенных ниже секущей линии, отражающих ситуацию ненасыщения (рис. 2.3б).

5. Аксиома непрерывности. Если , то наборы, достаточно близкие к (например, ), также должны предпочитаться (рис. 2.3 а). Данная предпосылка позволяет исследовать реакцию индивидов на относительно малые изменения дохода и цен.

6. Аксиома строгой выпуклости к началу координат (предпочтение среднего набора). Рисунок 2.3а представляет строго выпуклую кривую безразличия. Выпуклость можно описать с помощью математического понятия «выпуклый набор точек». Любые две точки на кривой безразличия можно соединить прямой. Набор , представленный средней точкой на отрезке с количествами благ , предпочитается любой из исходных комбинаций и , поскольку набор С лежит на более высокой кривой безразличия, следовательно, обладает большей полезностью.

Любая пропорциональная комбинация (взвешенная средняя) из двух товарных наборов, имеющих одинаковую полезность, предпочитает наборам с преобладающим удельным весом одного из товаров. Данная аксиома также отражает рациональный выбор потребителя.

Основным рабочим понятием порядковой теории полезности является предельная норма замещения. Предельная норма замещения для различных товаров ( - Marginal rate of substitution) измеряет пропорцию, в которой потребитель замещает один товар другим товаром, оставаясь при этом на кривой безразличия. Последнее означает, что полезность нового набора не изменяется. Потребление одного блага увеличивается (или уменьшается), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага.

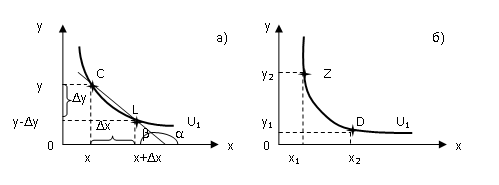
Рисунок 2.4 – Предельная норма замещенияError: Reference source not found

На рисунке 2.4а потребитель уменьшает потребление блага на и увеличивает потребление блага на , оставаясь на кривой безразличия. Благосостояние потребителя не изменяется. По определению предельная норма замещения измеряется отношением:

.

Такое отношение измеряет наклон кривой безразличия на дуге. Если величины и - бесконечно малые, то потребитель находится в точке, секущая занимает положение касательной, а предельная норма замещения одного товара другим принимает вид:

.

Предельную норму замещения можно измерить с помощью предельной полезности одного и другого блага. Пусть в наборе имеется два блага, а функция полезности . Уменьшив потребление блага на , полезность набора уменьшается на ; увеличив в наборе количество другого блага на , полезность набора увеличится на . Но общее изменение полезности будет равно нулю, так как наборы и находятся на одной и той же кривой безразличия. Поэтому . Отсюда

.

Аналогично в точке

Вопросы самоконтроля:

1. Перечислите основные положения количественной и порядковой теорий полезности

2. Как соотносятся между собою общая и предельная полезность товара. Ответ представьте графически и аналитически.

3. Перечислите и докажите аксиомы порядкового подхода.

4. Чем определяются форма и месторасположение кривых безразличия? Почему кривые безразличия не пересекаются?

5. Дайте определение следующим категориям: «полезность», «предельная полезность», «кривые безразличия», «предельная норма замещения».