4. Основні види вибірки та їх застосування в статистиці

За способом відбору одиниць для обслідування розрізняють такі різновиди вибіркового спостереження:

• власне випадкова вибірка (повторна та безповторна);

• механічна;

• типова (районована);

• серійна (гніздова);

• комбінована;

• моментне спостереження.

Власне випадкова вибірка. За такого способу відбору всі одиниці генеральної сукупності мають однакову можливість потрапити в досліджувану групу. Відбір одиниць проводять жеребкуванням.

Приклад власне випадкової безповторної вибірки — тираж виграшів грошово-речової лотереї: усі номери випущених лотерейних білетів кладуть в урну; ретельно перемішують і витягують із неї один за одним наперед задану кількість виграшних номерів.

Якщо, наприклад, потрібно визначити вік 1000 студентів, то на картки однакового розміру записують фактичний вік, кладуть картки в урну; витягнувши з неї одну картку, записують номер і знову кладуть картку в урну, ретельно перемішують картки, знову виймають одну й так до заданої чисельності вибірки. Це приклад повторної вибірки.

Механічна вибірка. Це різновид власне випадкової вибірки, коли всі одиниці генеральної сукупності розміщують у певному порядку:

• за алфавітом;

• часом реалізації (виробництва);

• розміщенням у просторі та ін.

Потім залежно від обсягу вибірки відбирають для дослідження кожну 2, 3, 4, 10-ту і т. д. одиницю.

Механічну вибірку широко застосовують для контролю якості продукції, відбору підприємств певної галузі для дослідження, під час бюджетних обстежень сімей.

Типова (районована) вибірка. Досліджувану генеральну сукупність розбивають на однорідні групи, райони чи зони. Потім із кожної групи випадково відбирають певну кількість одиниць пропорційно частці цієї групи в загальній сукупності.

Наприклад, відбираючи сім'ї для бюджетного обстеження, їх групують за видами економічної діяльності, а потім — за галузями промисловості, виробничими напрямками тощо.

Така процедура забезпечує потрапляння у вибірку представників усіх виділених типових груп, і вибірка стає більш достовірною.

Серійна (гніздова) вибірка. На практиці іноді замість відбору окремих одиниць відбирають цілі групи (гнізда), і вже в кожній групі спостерігають усі без винятку одиниці. Групи (гнізда) відбирають методом власне випадкової безповторної вибірки чи за допомогою механічного відбору.

Наприклад, з інкасаторської сумки випадково відбирають 10 пачок грошей по 100 купюр (це гнізда), а потім перевіряють кожну купюру на зношеність або автентичність.

Мала вибірка. Це несуцільне статистичне обстеження, коли вибіркову сукупність утворено з порівняно невеликої кількості одиниць генеральної сукупності. Обсяг малої вибірки зазвичай не перевищує 30 одиниць і може сягати 4-5 одиниць.

Помилки малої вибірки визначають за формулами, що відрізняються від формул для вибіркового спостереження з порівняно великим обсягом вибірки . Середню помилку малої вибірки обчислюють за формулою

де — дисперсія малої вибірки.

Відомо, що оскільки в разі малої вибірки множник суттєвий, то дисперсію малої вибірки обчислюють з урахуванням степенів вільності. Під кількістю степенів вільності розуміють кількість варіантів, які можуть набувати довільного значення, не змінюючи середньої. У разі визначення дисперсії кількість степенів вільності дорівнює :

Граничну помилку малої вибірки визначають за формулою

При цьому значення коефіцієнта довіри залежить не тільки від заданої довірчої ймовірності, але й від чисельності вибірки .

Для окремих значень й довірчу імовірність малої вибірки визначають за таблицями Стьюдента, у яких наведено дані розподілу стандартизованих відхилень:

Значення таблиць Стьюдента характеризують імовірність того, що гранична помилка малої вибірки не перевищує — кратну середню помилку:

Проводячи малі вибіркові обстеження, важливо мати на увазі те. що зі зменшенням обсягу вибірки збільшуються розбіжності між розподілом Стьюдента та нормальним розподілом. За мінімального обсягу вибірки ця розбіжність суттєва, що зменшує точність результатів малої вибірки.

Користуючись малою вибіркою, визначають межі генеральної середньої досліджуваної ознаки.

Середню помилку малої вибірки визначають за формулою

Для наведених у прикладі даних

Наприклад, проведено вибірку обсягом 20 одиниць. Вибірковий середній квадрат відхилення = 80. Обчислимо вибіркове середнє квадратичне відхилення малої вибірки:

У статистиці застосовують також моментний, багатоступеневий і багатофазовий види відбору. Різні форми організації відбору одиниць у вибіркову сукупність — це подальший розвиток і видозміни простого випадкового відбору. Застосування того чи іншого виду відбору залежить від характеру об’єкта спостереження, а також бажання здешевити чи полегшити процес спостереження.

Способи поширення вибіркових даних па генеральну сукупність. Кінцева мета вибіркового спостереження — поширення його характеристик па генеральну сукупність. Є декілька способів поширення вибіркових даних.

Якщо треба визначній обсяг ознаки в генеральній сукупності, роблять прямий розрахунок. Середній розмір ознаки, обчислений у результаті вибіркового спостереження, множать на чисельність одиниць генеральної сукупності.

Наприклад, у 3-процентній вибірці чисельністю 150 світильників шість виявилися бракованими (помилка вибірки — один світильник). За часткою браку у вибірковій сукупності ((6/150) • 100 = 4 %) можна визначити, скільки бракованих світильників у генеральній сукупності обсягом 5000:

(5000 • 4)/100 = 200.

Якщо вибіркове спостереження проводять для уточнення результатів суцільного спостереження, застосовують метод коефіцієнтів.

Нехай суцільний перепис (облік) показав, що в районі у приватній власності населення налічується 3000 корів. Під час контрольної перевірки 10% дворів (вибіркового спостереження) було виявлено, що під час суцільного спостереження в цих господарствах було зафіксовано 250 корів, а під час контрольного — 254. Отже, виявлено, що під час суцільного перепису не враховано чотири голови, що становить 1,6 % (4/250). Тоді 101,6 %— поправковий коефіцієнт, застосовуючи який, можна обчислити кількість корів у приватній власності населення району:

3000 * 101,6/100 = 3048. Відбір вважають задовільним, якщо гранична помилка репрезентативності не перевищує 2-5 %. Якщо помилка більша ніж 5 %, вибірку вважають нерепрезентативною й повторюють відбір. Якщо й повторний відбір не дає позитивних результатів, то для підвищення репрезентативності доцільно збільшити чисельність вибіркової сукупності.

Вибіркові значення розповсюджують па генеральну сукупність з урахуванням довірчих інтервалів. Для цього відповідні узагальнювальні показники вибіркової сукупності w та х корегують на граничну помилку вибірки та

• для частки альтернативної ознаки

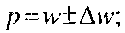
• для середньої величини кількісної ознаки

Методи формування вибіркової сукупності — важливий чинник, від якого залежить репрезентативність вибірки, а методи відбору одиниць у вибірку дають змогу підвищити точність характеристики та визначити оптимальну чисельність вибіркової сукупності в маркетинговій, правовій, фінансово-банківській та іншій діяльності.

Питання для самоконтролю

1. Що являє собою варіація ознаки? Від чого залежать її значення?

2. Чому важливо знати варіацію для характеристики досліджуваної сукупності?

3. У яких випадках використовують показники варіації?

4. Що таке розмах варіації? Наведіть формулу. Поясніть економічний зміст.

5. Що таке середнє лінійне відхилення? Наведіть формулу. Продемонструйте техніку обчислення. Поясніть економічний зміст.

6. Що таке дисперсія? Як її інакше називають в статистиці? Наведіть формулу. Продемонструйте техніку обчислення. Чи має дисперсія економічний зміст?

7. Що таке середнє квадратичне відхилення? Наведіть формулу. Продемонструйте техніку обчислення. Чи має середнє квадратичне відхилення економічний зміст?

8. Чи можна визначити середнє квадратичне відхилення, якщо відомі розмах варіації чи середнє лінійне відхилення?

9. Що таке квадратичний коефіцієнт варіації? Наведіть формулу. Продемонструйте техніку обчислення. Поясніть економічний зміст.

10. Назвіть основні види коефіцієнтів варіації.

11. На чому ґрунтуються спрощені способи обчислення дисперсії?

12. Що станеться з дисперсією, якщо зменшити чи збільшити кожне конкретне значення усереднюваної ознаки на одну й ту саму величину?

13. Що станеться з дисперсією, якщо зменшити чи збільшити кожне конкретне значення усерднюваної ознаки в одну й ту саму кількість разів?

14. Запишіть формулу обчислення середнього квадратичного відхилення способом моментів. Покажіть уміння користуватися нею.

15. Запишіть символами таку властивість дисперсії: дисперсія ознаки дорівнює різниці між середнім квадратом значень ознаки і квадратом їх середньої. Проілюструйте правильність цієї властивості.

16. Що таке міжгрупова дисперсія? Наведіть формулу. Продемонструйте техніку обчислення.

17. Як визначити внутрішньогрупові дисперсії та середню цих дисперсій? Наведіть формулу. Продемонструйте техніку обчислення.

18. Сформулюйте правило складання дисперсій. У чому полягає його практичне значення?