Фильтр Чебышева второго рода
Ф-ия передачи этого
фильтра имеет и нули, и полюсы. Она
связана с ф-ей передачи фильтра первого
рода следующим образом:
Полюсы передачи
фильтров 1 и 2 рода тоже связаны:
По этой причине фильтр 2 рода наз-ют инверсным фильтром Чебышева.
АЧХ фильтра:
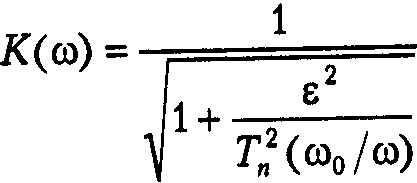
ω0 – частота среза; Tn(x) – полином Чебышева n-го порядка;
n – порядок фильтра; ε – параметр, определяющий величину пульсаций АЧХ в полосе задерживания.
А ЧХ в полосе пропускания (при |ω|≤ω0 ) монотонно затухает, а в полосе задерживания колеблется между 0 и значением
Значение параметра ε и уровень пульсаций связаны:
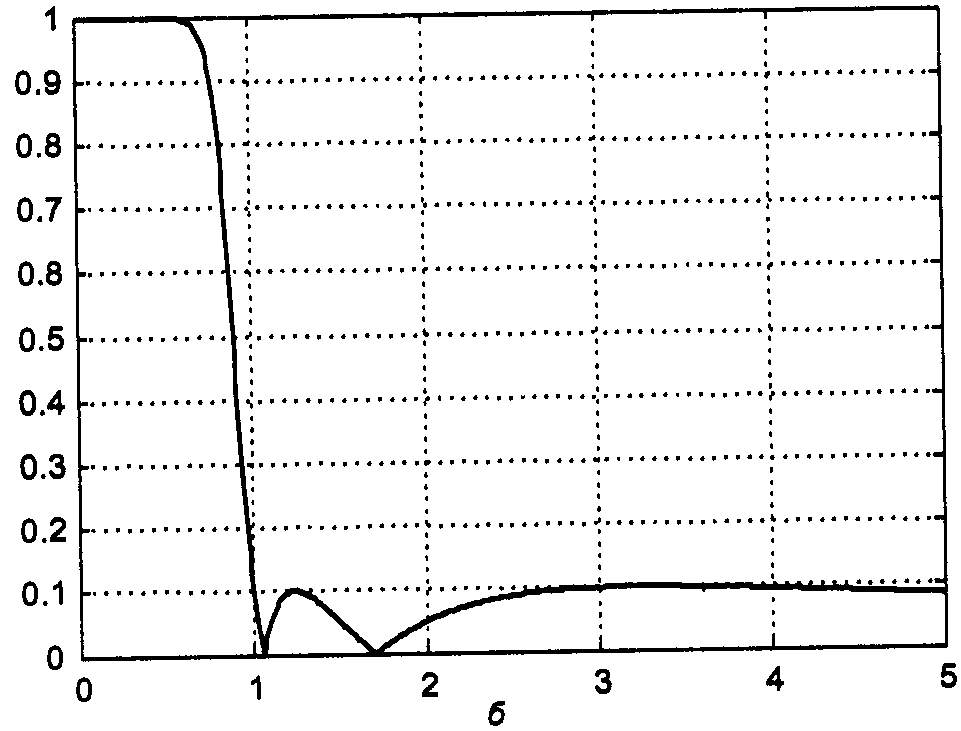
Эллиптический фильтр (фильтр Кауэра)
Объединяет в себе св-ва фильтров Чебышева 1 и 2 рода. За счёт этого удаётся обеспечить максимально возможную крутизну скачка АЧХ, то есть переходной зоны между полосами пропускания и задерживания.
АЧХ фильтра:
ω0 – частота среза; n – порядок фильтра; Rn(…) – рациональная ф-ия Чебышева n-го порядка; ε и L – пар-ры, определяющие величину пульсаций в полосах пропускания и задерживания.
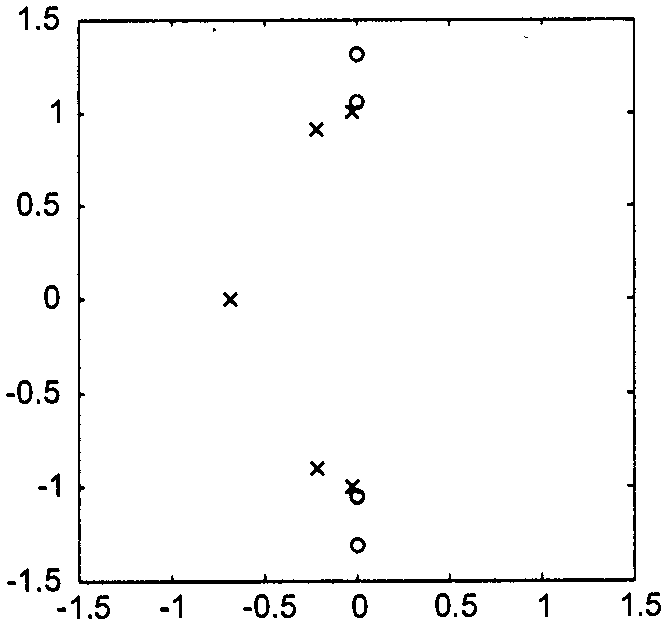
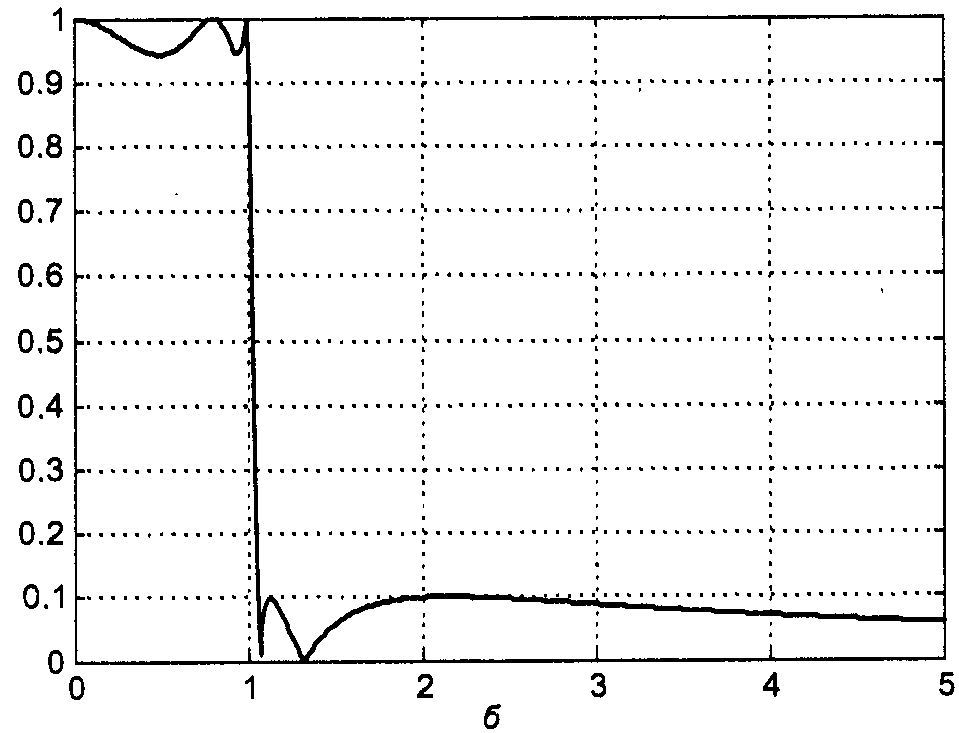
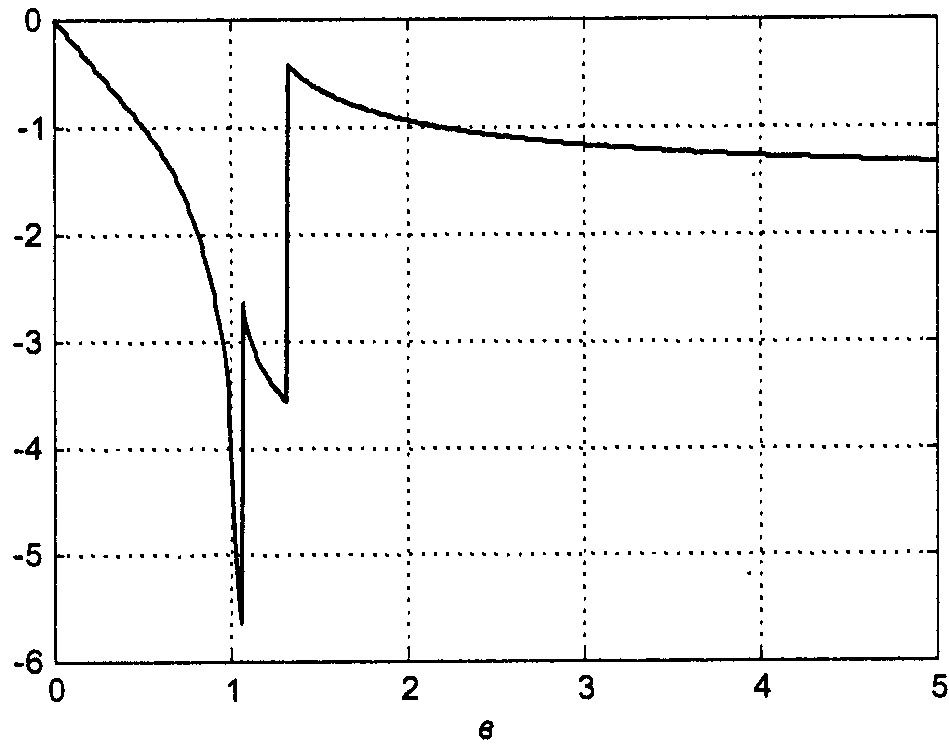
Фильтр Бесселя
Ценность этого фильтра в том, что для него зависимость группового времени задержки от частоты явл-ся максимально гладкой в точке ω = 0, и групповая задержка очень мало меняется в полосе пропускания.
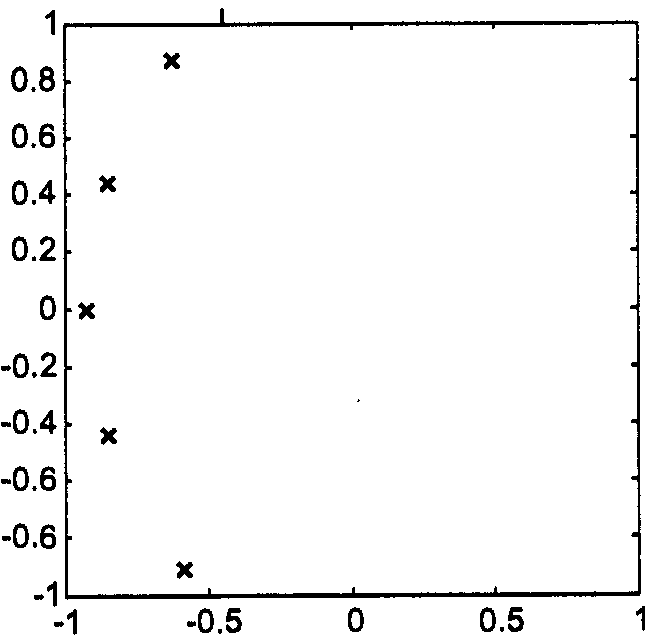
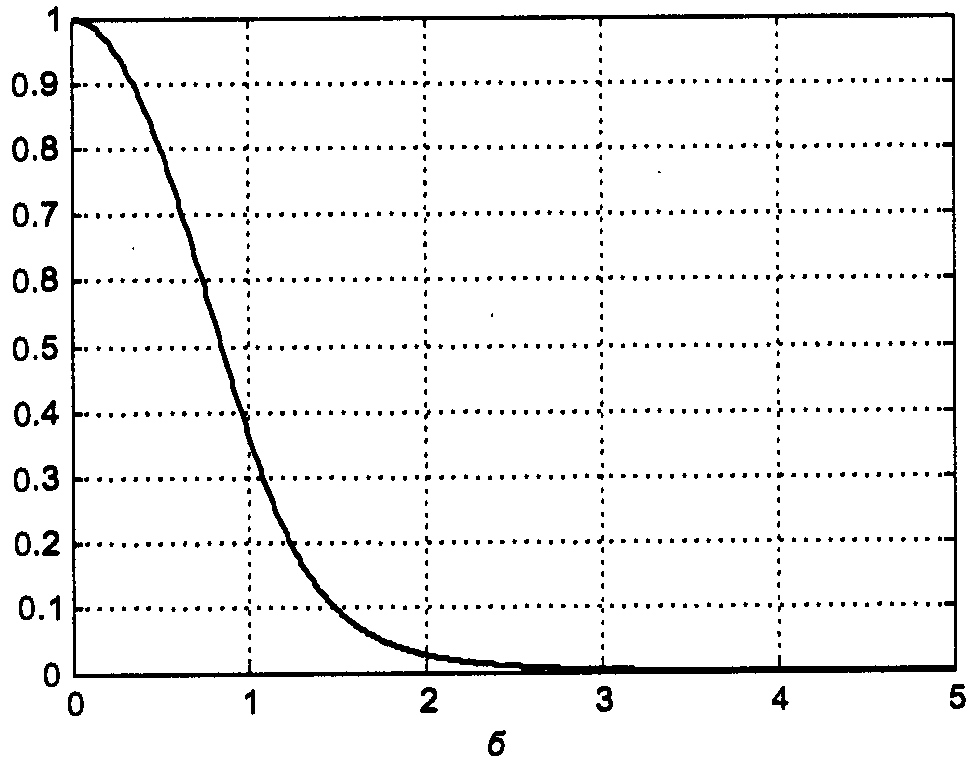
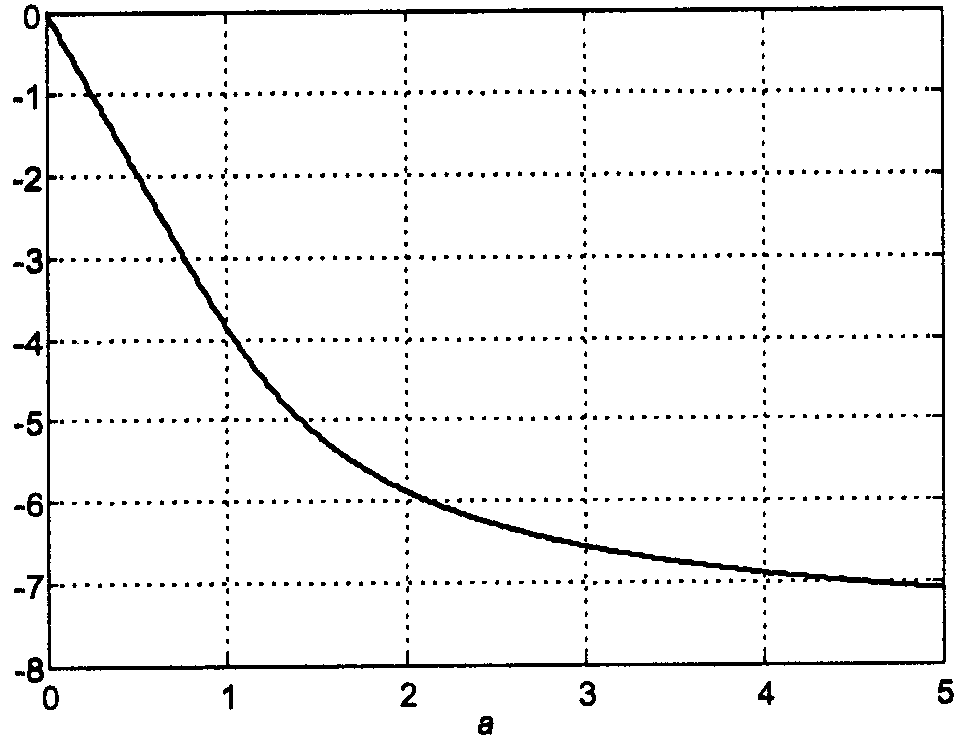
Ф-ия передачи фильтра:
,
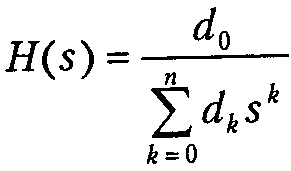где
Далее рассмотрены преобразования фильтров – прототипов.
Изменение частоты среза ФНЧ
С
водится
к простому масштабированию частотной
оси заменой переменной S:
где ω0 – требуемая частота среза ФНЧ.
Преобразование ФНЧ в ФВЧ
Требует инверсии
частотной оси, путём замены:
где ω0 – требуемая частота среза ФВЧ.
Преобразование ФНЧ в полосовой фильтр
,
где
,
ω1 и ω2 – соответственно нижняя и верхняя границы полосы пропускания фильтра.
Преобразование ФНЧ в режекторный фильтр
,
где
,
ω1 и ω2 – нижняя и верхняя границы полосы задерживания фильтра.
№7
Z - преобразование
Оно явл-ся удобным способом анализа дискретных последовательностей. Смысл его в том, что последовательности чисел {x(k)} ставится в соотв-ие ф-ия комплексной переменной z, определяемая так:
Ф-ия X(z) определена только для тех значений z, при которых ряд сходится.
Z – преобразование единичной импульсной ф-ии
Единичная импульсная ф-ия – это дискретный аналог дельта – функции, представляет собой одиночный отсчёт с единичным значением:
Его Z – преобразование:
Z – преобразование единичного скачка
Его Z – преобразование:
Ряд представляет собой бесконечную геом. прогрессию с первым членом
1*z-0 = 1, и знаменателем z-1. Ряд сходится при |z|>1. Его сумма:
Z – преобразование дискретной экспоненты
Это тоже геометрическая прогрессия. Первый член = 1, знаменатель = az-1. Ряд сходится при |az-1|<1, т.е. при |z|>|a|, а его сумма равна:
Связь Z – преобразования с преобразованием Лапласа и Фурье
Рассмотрим
последовательность, определённую при
k≥0,
и сопоставим ей временной сигнал в виде
набора дельта – функций:
,
где Т – интервал дискретизации
Преобразование Лапласа для этого сигнала:
Воспользовавшись фильтрующим св-вом дельта ф-ии получим:
Эта формула переходит в формулу для Z – преобразования, если выполнить подстановку z = epT
Таким образом, связь между Z – преобразованием и преобразованием Лапласа:
Связь между Z – преобразованием и преобразованием Фурье:
Свойства Z – преобразования
1) Линейность
2) Задержка
Если Z – преобразование последовательности {x(k)} равно X(z),
то z-преобразование послед-ти, задержанной на k0 тактов (y(k)=x(k-k0)), будет таким:
То есть появляется оператор задержки z-k0