Пример графа регулярной вычислительной системы представлен на рисунке 1.2.1.

Определение 1.2.10. Диаметр d – это максимальное расстояние, определяемое как

d = max{r_i,j}, i,j {0,…,N-1},

где r_i,j – расстояние между вершинами i, j графа рассматриваемой ВС.

Расстояние r_i,j есть минимальная длина простой цепи между вершинами i, j, где длина измеряется в количестве ребер между вершинами i, j.

Например, на рисунке 1.2.1 длины между вершинами (0,5) есть 3 ((0,1),(1,2),(2,5)), 2 ((0,1),(1,5)), 2 ((0,4),(4,5)), 3 ((0,3),(3,4),(4,5)), 3 ((0,3),(3,6),(6,5)), 2 ((0,6,),(6,5)) и др., длина которых больше 3-х. Следовательно, расстояние r_i,j равно 2. При рассмотрении всех возможных расс тояний определяется d=2.

Рисунок 1.2.1. Пример графа регулярной вычислительной системы

Определение 1.2.11. Средний диаметр di для i-й выделенной вершины определяется как

(1.2.1)

где p_i – расстояние от текущей до i-й выделенной вершины, – число вершин, находящихся на расстоянии p _i от выделенной.

Определение 1.2.12. Средний диаметр для графа вычислительной системы определяется в виде:

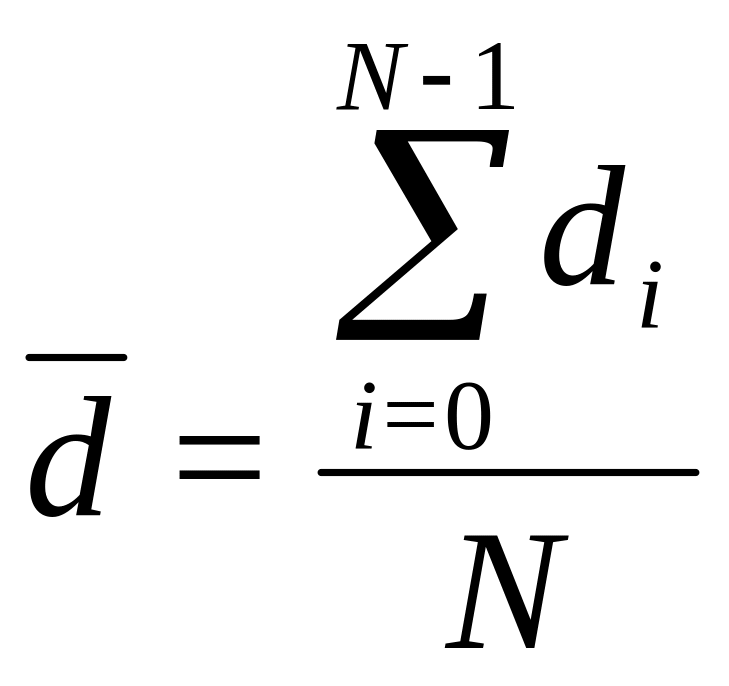
Примечание: Для регулярной вычислительной системы

Сеть S должна обеспечивать в каждый момент времени, требуемый обмен данными между вычислительными модулями. Наиболее подходящей для этой цели является сеть по полному графу, т.е. связь каждого вычислительного модуля с каждым. Построение такой сети для большого количества вычислительных модулей, содержащихся в современных ВС, является сложной и дорогостоящей процедурой. В связи с чем, разрабатываются различные типы и конфигурации сетей, в которых обеспечиваются связи в зависимости от различных требований. Очевидно, что в таких сетях, как правило, возникает необходимость транзитной передачи информации с помощью вычислительных модулей, попадающих в контур передачи информации. Такие передачи, естественно, требуют дополнительных затрат времени, в связи с чем возникает задача минимизации этих затрат c помощью выбора конструкций тех или иных разновидностей сетей с учетом структуры решаемых задач. Вследствие этого проблему выбора графа межмодульных связей необходимо рассматривать в нескольких аспектах:

• минимизация времени выполнения межмодульных обменов;

• максимизация числа одновременно выполняемых обменов;

• максимальная сохранность связности при выходах из строя ВМ и линий.

Таким образом, в качестве критериев выбора графа логично выбрать диаметр и средний диаметр графа. Диаметр графа определяет максимально необходимое число транзитных передач, а средний диаметр – среднюю длину транзитного пути. В качестве показателя, оценивающего вероятность существования межмодульных связей в графе (при заданных значениях коэффициентов готовности ВМ и линий, компоненты связности, включающей не менее 0, 1, 2, …, N-1 вершин, где N – количество вычислительных модулей в системе), используется вектор-функция структурной живучести графа. При определении данного показателя необходимо произвести достаточно сложные вычисления. По результатам моделирования оказалось, что минимизация обоих диаметров является необходимым условием максимизации координат вектор-функции структурной живучести графа. Поэтому в качестве критерия выбираются диаметр и средний диаметр.