11.6.Определение функций плотности загрузки, и минимальной загрузки для информационных граф-схем

Исследование проблемы загрузки вычислительных модулей в ВС является достаточно сложным процессом. С одной стороны, должны быть учтены многие факторы, связанные с функционированием ВС, с другой – с выполнением параллельной программы. Оценим временные затраты, а также необходимое число ВМ, исходя из условия, что время, затрачиваемое на выполнение оператора тратится ровно столько, сколько указано в весе оператора. Зададим области определения операторов граф-схемы. Отдельный оператор t_j задан в области t_1,j ≤ t_j ≤ t_2,j

Пусть А – множество начальных вершин, В – множество конечных вершин.

Зададим области определения интервалов времени выполнения операторов для множества вершин графов в виде трёх неравенств.

t_j ≥ p_j , j A. (6.1.1)

t_j – p_j ≥ t_i , если существует связь i→j , i X\B, j X\ A. (6.1.2)

tj ≤ T, если j B, (6.1.3)

где T – время решения задач. Эта система неравенств определяет многоугольник М_Т в RS-мерном пространстве. Если точка (t₁, ..., t_RS) M_T, то она удовлетворяет системе неравенств (6.1.1), (6.1.2), (6.1.3). RS – размер матрицы S.

Определение 6.1.3. Функция t₁, t₂, …, t_RS, ) = , где OP(t_j,)=  плотностью загрузки вычислительной системы для значений {t₁, …, t_RS} в точке .

В качестве примера вычисления функции PZ рассмотрим диаграмму рисунка 6.1.2.а. Значение функции PZ(1, 3, 5, 6, 8, 6, 8, 16, ) при  =1 равно единице, при  =3 равно двум, при  =6 равно трём.

Зафиксируем моменты окончания выполнения операторов таким образом, чтобы точки (t₁, t₂, …, t_RS ) M_T. Значение функции PZ в каждый момент времени формируется в том числе операторами множества ВНО, т.е. в каждый момент времени значение функции PZ совпадает с числом одновременно выполняемых операторов.

Вычислим Q = max{ q₁, …, q_s}, где q_i –множество ВНО, тогда можно утверждать, что

Q = t₁, t₂, …, t_RS, ), (6.1.4)

так как возможна ситуация, когда выполняются все операторы максимально полного множества ВНО. Учитывая соотношение (6.1.4), сформулируем лемму 6.1.1.

Лемма 6.1.1. Минимальное число N вычислительных модулей однородной ВС, способных выполнить данный алгоритм за время Т Т_кр не превышает f, где f – количество элементов в максимально полном множестве ВНО.

Определение 6.1.3. Функция Z(t₁, …, t_RS, a, b)= t₁, …, t_RS, ) d называется загрузкой отрезка [a, b] [0, T] для точки (t₁, …, t_RS) M_T.

С помощью функции Z определяется загрузка отрезка [a,b], выполняемыми на этом отрезке операторами.

Определение 6.1.4. Функция Z^(T)(a, b)= называется минимальной загрузкой отрезка [a, b] [0, T] для точки (t₁, …, t_RS) M_T.

Смысл этого определения заключается в том, что при любом планировании операторов для выполнения при решении задачи за время Т, загрузка отрезка

[a, b] [0, T] не может быть меньше вычисленной величины.

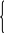Для составления алгоритма вычисления данной функции введем функцию :

x при х 0

=

0 при х < 0

При выборе интервалов для определения минимальной загрузки время окончания выполнения оператора размещается на отрезке [t_1,j, t_2,j], который случайным образом ложится на рассматриваемый интервал, поэтому целесообразно различные случаи относительного размещения интервалов [a, b]и [t_{1, j}, t_{2, j}]. Все возможные ситуации представлены на рисунке 6.1.3.

t_{1, j}-p_j a t_{1, j} t_{2, j}(T) b t a t_{1, j}-p_j t_{2, j}(T)-p_j b t_{2, j}(T) t

a) б)

t_{1, j}-p_j a t_{2, j}(T)-p_j t_{1, j} b t_{2, j}(T)

в)

а t_{1, j}-p_j t_{2, j}(T) b t t_{1, j}-p_j t_{2, j}(T)-p_j a b t_{2, j}(T) t

г) д)

Рисунок 6.1.3. Относительное размещения интервалов [a, b] и [t_{1, j}, t_{2, j}].

На рисунке 6.1.3.а оператор при раннем сроке окончания выполнения оператора попадает в рассматриваемый интервал частично. На рисунке 6.1.3.б оператор при позднем сроке окончания выполнения оператора попадает в рассматриваемый интервал частично. На рисунке 6.1.3.в оператор при раннем сроке его окончания и позднем сроке окончания попадает в рассматриваемый интервал частично. При определении минимальной функции загрузки необходимо выбрать его минимальную часть. На рисунке 6.1.3.г оператор попадает в рассматриваемый интервал полностью, поэтому время выполнения оператора включается полностью в рассматриваемый интервал. На рисунке 6.1.3.д оператор включает рассматриваемый интервал полностью, поэтому вклад оператора в загрузку определяется длиной рассматриваемого интервала.

Алгоритм вычисления функции минимальной загрузки отрезка Z^(T)(a, b).  

Алгоритм 6.1.3.

1. С помощью алгоритмов 6.1.1 и 6.1.2 вычисляются ранние t_1,j и поздние t_{2, j}(T) сроки окончания выполнения операторов.

2. Полагаем Z^(T)(a, b):=0.

3. Анализируем последовательность операторов j:=1, …,RS.

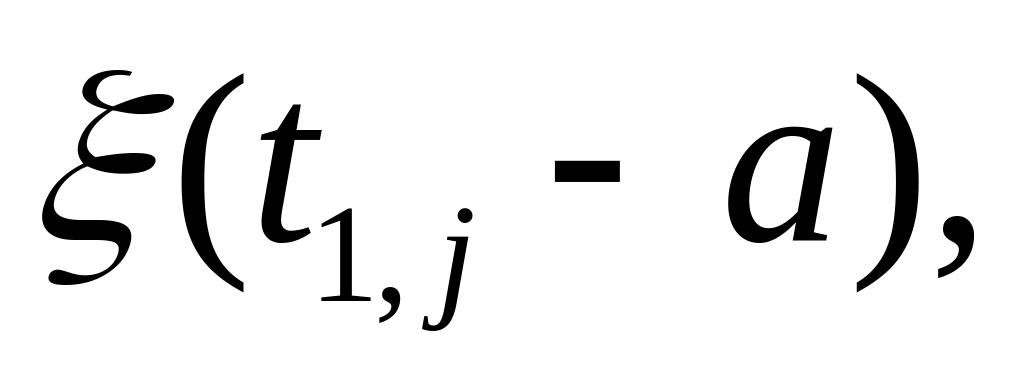
4. Вычислим Z^(T)(a, b):= Z^(T)(a, b)+min{ 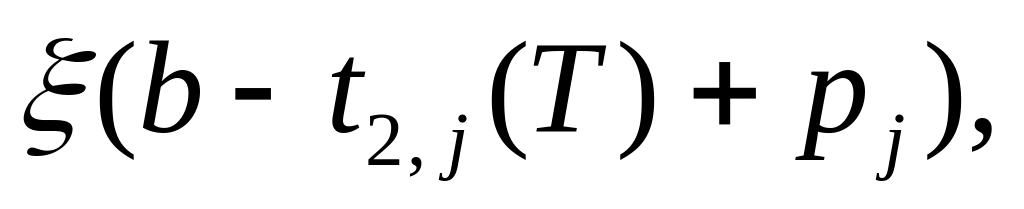p_j, b-a }

5. После перебора всех операторов получаем значение Z^(T)(a, b).  

При разработке и эксплуатации ВС одним из основных вопросов является определение требуемого количества ВМ для решения поставленной задачи за время Т или при заданном количестве ВМ определить, сколько потребуется времени для решения задачи. Ответ на этот вопрос дают две теоремы Барского [4].

Теорема 6.1.1. «Об оценке снизу числа ВМ, необходимых для решения задачи за время Т ».

Для того чтобы N вычислительных модулей было достаточно для выполнения заданного алгоритма за время Т необходимо, чтобы для отрезка[a, b] [0, T] выполнялось соотношение

Z^(T)(a, b) N(b-a) (6.1.5)

Доказательство. Согласно лемме 6.1.1 существует неравенство

t₁, t₂, …, t_RS, ) N. (6.1.6)

Для любого отрезка времени [a, b] [0, T]согласно определению 6.1.4 справедливо неравенство

Z^(T)(a, b) Z(t₁, …, t_RS, a, b). (6.1.7)

По определению 6.1.3:

Z(t₁, …, t_RS, a, b)= t₁, …, t_RS, ) d . (6.1.8)

Заменив, используя неравенство (6.1.6), подынтегральную функцию выражения (6.1.8) значением N, и учитывая неравенство (6.1.6), получим выражение (6.1.5).

Отсюда

N Z^(T)(a, b)/ (b-a) .

Необходимость, но недостаточность условия теоремы 6.1.1 можно продемонстрировать на следующем примере. Пусть задана граф-схема в виде, представленном на рисунке 6.1.4.

1 1 1

1 1 1

0 1 2 3

Рисунок 6.1.4. Иллюстрация выполнения условия необходимости и достаточности к теореме 6.1.1.

Определим число ВМ, необходимых для решения задачи, представленной граф-схемой на рисунке 6.1.4 Для этого проанализируем минимальную загрузку интервалов [0,1], [1, 2], [2, 3], [0, 2], [1, 3] и [0, 3]:

Z⁽³⁾(0, 1)= Z⁽³⁾(1, 2)= Z⁽³⁾(2, 3)=0, Z⁽³⁾(0,2)= Z⁽³⁾(1, 3)=3, Z⁽³⁾(0, 3)=6.

Согласно теореме 6.1.1 требуется два ВМ. Разместить операторы диаграммы, представленной на рисунке 6.1.4 на двух ВМ, не представляется возможным.

Теорема 6.1.2. «Об оценке снизу времени выполнения задачи при заданном количестве процессоров».

Если Т₁ – оценка снизу времени выполнения алгоритма, представленного информационным графом со скалярными весами вершин на ВС, имеющей N процессоров, и на отрезке [a, b] [0, T] выполняется соотношение

тогда наименьшее время Т реализации алгоритма удовлетворяет соотношению

Т .

Доказательство. Найдём величину g>0, такую, чтобы объём работ выполнялся и при значении Т=Т₁+g на интервале [a, b+g], но так же выполнилось условие (6.1.5):

тогда , отсюда получим g=d/N.

Алгоритм определения оценки минимального числа процессоров, необходимого для выполнения алгоритма за время Т, составленный на основании теоремы 6.1.1.

Алгоритм 6.1.4.

1. Вычислить N:=0.

2. Последовательно берутся интервалы [a, b] [0, T] в порядке:

[0,1]

[0,2], [1,2],

[0,3], [1,3], [2,3]

…

[0,T], [1,T],…, [T-1,T]. Всего отрезков: Т(Т+1)/2.

3. Для очередного интервала [a, b] вычислим N1= Z^(T)(a, b) / (b-a) , где Z^(T)(a, b)

определяется по алгоритму 6.1.3.

4. Если N1>N, то N:= N1.

5. После обработки всех интервалов, получается требуемое N .

Алгоритм определения оценки минимального времени Т выполнения заданного алгоритма на ВС, содержащей N процессоров, составленный на основании теоремы 6.1.2.

Алгоритм 6.1.5.

1. Вычислим Т:=Т_кр.

2. Просматриваются интервалы [a, b] [0, T], как в алгоритме 6.1.4 пункте 2.

Примечание. При таком выборе последовательности отрезков значение T можно увеличивать, не пересчитывая при этом ранее вычисленные значения d.

2. Для очередного интервала [a, b]вычислим значение

d:= Z^(T)(a, b)-N(b-a),

где Z^(T)(a, b) определяется по алгоритму 6.1.3.

2. Если d>0 вычисляется

T:=T+]d/N[.

где ]x[ – ближайшее целое, не меньшее x.

5. Вычислим t_{2, j}(T):= t_{2, j}(T)+]d/N[, j=1, …, RS

6. После обработки всех интервалов вычисляем значение Т – нижнюю оценку

минимального времени выполнения данного алгоритма на данной ВС.