1.3.13. Вычислительные системы с сетью связей типа «Граф л(n,V,g)»

Построение графа Л(N,v,g) осуществляется следующим образом: выбирается некоторый подграф бесконечного планарного графа L(v,g), содержащий N вершин. Вершины подграфа, имеющие степень меньше, чем v, соединяются рёбрами так, чтобы степени этих вершин стали равными v. Таким способом из бесконечного планарного графа L(v,g) можно построить множество графов Л(N,v,g), среди которых выбирается граф Л(N,v,g) с минимальным числом простых циклов, длина которых отличается от g.

Рассмотрим алгоритм построения бесконечного планарного графа L(v,g) [1,2] более подробно:

Заданы: степень вершин графа v; обхват графа g; количество ярусов NY, которые будут построены. Введем переменную NG общего числа вершин графа; матрицу s[i,j] номеров j-ых вершин на i-ых ярусах графа; матрицу X(i,j) свободных связей j-ых вершин на i-ых ярусах; матрицу B(i,j) текущих степеней j-ых вершин на i-ых ярусах; матрицу A(s[i,j], s[p,q]) смежностей вершин; вектор N(i) – число вершин на i-м ярусе. Пусть i – номер текущего яруса, j – номер текущей вершины на ярусе. Здесь окружность соответствует ярусу.

1. Исходные значения: обнуляем X(n,m), B(n,m), A(k,k), N(n).

2. Выбираем точку на плоскости, представляющую вершину s[0,0] – единственная вершина нулевого яруса. Полагаем N[0]:=1; NG:=1. s[0,0]:=0.

3. Номер текущего яруса i:=1. Количество вершин на первом ярусе N[1]:=v; NG:=NG+N[1].

4. Строим первую окружность (ярус) с центром в вершине s[0,0]. Разбиваем ее на v разных частей v точками. Размещаем в каждой точке вершины s[1,k], . Причем вершина s[1,k] располагается между s[1,(k-1)mod v] и s[1,(k+1)mod v], то есть вершины следуют по порядку. Вычисляем s[1,k]:=N[0]+k, .

5. Строим ребра (s[0,0]; s[1,k]), , то есть соединяем центральную вершину s[0,0] со всеми вершинами первого яруса. Формируем матрицу смежности A[0,s[1,k]]:=1; A[s[1,k], 0]:=1.

6. Проверяем, построены ли все ярусы: i>NY. Если да, то переходим на шаг 15, иначе – шаг 7.

7. Вычисляем i:=i+1. Строим i-ю окружность с центром в вершине s[0,0]. Полагаем j:=0; N[i]:=0.

8. Проверяем, существует ли j-я вершина предыдущего (i-1)-го яруса: j<N[i-1]. Если да, то переходим на шаг 9. Иначе – NG:=NG+N[i] и переход на шаг 15.

9. Вычисляем для вершины s[i-1,j]: степень , количество оставшихся свободных связей X[i-1,j] := v - B[i-1,j]. Вычислим количество вершин, которые необходимо построить на текущем i-ом ярусе: N[i] := N[i] + X[i-1,j].

10. Вычисляем j := j +1. Переход на шаг 8.

11. Разбиваем i-ю окружность N[i] точками на N[i] равных частей. В каждой точке размещаем вершины s[i,k], . Причем вершины следуют по порядку, то есть s[i,k] располагается между вершинами s[i,(k-1)mod N[i]] и s[i,(k+1)mod N[i]]. Вычисляем , .

12. Строим ребра:

Формируем матрицу смежности:

13. Если при слиянии двух соседних вершин i-го яруса s[i,k] и s[i,(k+1)mod N[i]], образуется простой цикл длины g, то эти вершины сливаются; количество вершин i-го яруса уменьшается на 1: N[i] := N[i] – 1. Перенумеровываем вершины.

Если проверены все возможные слияния вершин, то переход на шаг 14. Иначе – на шаг 13.

14. Если при соединении двух соседних вершин i-го яруса s[i,k] и s[i,(k+1)mod N[i]], ребром (s[i,k]; s[i,(k+1)mod N[i]]) образуется простой цикл длины g, то такое ребро вводится в граф. Если введены все возможные ребра, то переходим на шаг 6. Иначе – переход на 14.

15. Конец алгоритма.

Схема данного алгоритма представлена на рисунках 1.3.17 и 1.3.18.

На вход алгоритма (процедура PPG (v,g,NY)) подаются параметры v, g и NY. Алгоритм выдает результат работы в графическом виде – планарный граф L(v,g) с заданным количеством ярусов NY.

Рассмотрим процедуры, входящие в рассматриваемый алгоритм.

Процедура ODC – основная процедура – определяет длину простого цикла в графе. Входные данные – пара соседних вершин s[i,k] и s[i,(k+1)mod N[i]]. Выдает она – длину простого цикла g1, который образуется при слиянии пары этих вершин в одну. Для определения цикла в графе можно было бы использовать один из широко известных методов, например, поиск в глубину. Однако подобные алгоритмы имеют большую вычислительную сложность. Зная закономерность расположения вершин в графе, можно построить алгоритм значительно проще:

1. Пусть g1:=0; f0:=s[i,j]; fk:=s[i,(k+1)mod N[i]]. SM:=f0 – множество просмотренных вершин.

2. Проверяем f0=fk? Если да, то переходим на шаг 6. Иначе – шаг 3.

3. Используя матрицу смежности A[f0,k], , найдем {fl} – множество вершин, смежных с f0. Удалим просмотренные вершины: {fl}:={fl}\SM.

4. Определим ярусы {yl}, которым принадлежат вершины из {fl}. Выберем из множества ярусов {yl} максимальный ярус – y_max и множество вершин {fl}_max, принадлежащих этому ярусу. Из множества {fl}_max выбираем вершину с минимальным номером – fmin.

Полагаем: f0:=fmin; SM:=SM+{fmin}; g1:=g1+1. Переходим на шаг 2.

5. Простой цикл пройден. Его длина равна g1. Конец алгоритма.

Остальные процедуры носят вспомогательный характер:

Процедура RV – рисует N[i] вершин на i-ом ярусе графа. Реализуется при помощи графических средств языка программирования. Также здесь предполагается расчет порядкового номера вершины в графе на основании ее номера в яруса k и номера яруса i:

,

Процедура RR – рисует ребро между заданными вершинами s[i-1,j] и s[i,j1]. Реализуется также при помощи графических средств языка программирования. Дополнительно необходимо вычислить элементы матрицы смежности, так как введение ребра влияет на смежность вершин: A(s[i-1,j], s[i,j1]):=1 и A(s[i,j1], s[i-1,j]):=1.

Процедура OSV – определяет степень j-ой вершины (i-1)-яруса. Использует матрицу смежности A. Выдает матрицу степеней: B[i-1,j]:=B[i-1,j]+A[s[i-1,j],f], f=0, … , N[i-1]-1.

Процедура Summa – вспомогательная процедура для определения вершин, которые соединяются ребрами (пункт 12 алгоритма построения бесконечного планарного графа L(v,g)). На вход подаются – i, j, X. Процедура выдает результат R:= .

Процедуры SV – перерисовывает граф при слиянии двух вершин s[i,k] и s[i,(k+1)mod N[i]]. Реализуется при помощи графических средств языка программирования.

Процедуры DR – дорисовывает введенные ребра графа, соединяющие вершины s[i,k] и s[i,(k+1)mod N[i]]. Реализуется при помощи графических средств языка программирования

Рисунок 1.3.15. Схема алгоритма построения бесконечного планарного графа L(v,g)

Рисунок 1.3.18. Продолжение схемы алгоритма построения бесконечного планарного графа L(v,g)

Пример 1. Рассмотрим построение трёх ярусов бесконечного планарного графа L(4,5).

Исходные данные: v=4; g=5; NY=3.

1) Обнуляем X(n,m), B(n,m), A(k,k), N(n). Присваиваем v=4; g=5; NY=3.

2) Строим на плоскости вершину s[0,0]=0; N[0]:=1; NG:=1.

3) i:=1 (первый ярус); N[1]:=4; NG:=1.

4) Вершины на первой окружности: s[1,0]=1, s[1,1]=2, s[1,2]=3, s[1,3]=4.

5)Ребра: (s[0,0]; s[1,0]), (s[0,0]; s[1,1]), (s[0,0]; s[1,2]), (s[0,0]; s[1,3]). Построенный фрагмент графа представлен на рисунке 1.3.19.

Рисунок 1.3.19. Один ярус графа L(4,5)

Формируем матрицу смежности: A[0,1]:=1, A[0,2]:=1, A[0,3]:=1, A[0,4]:=1.

6) i=1 < 3, переход на шаг 7.

7) i:=2 (второй ярус);

8), 9), 10) j=0: B[1,0]:=1, X[1,0]:=4-1=3, N[2]:=0+3=3;

j=1: B[1,1]:=1, X[1,1]:=4-1=3, N[2]:=3+3=6;

j=2: B[1,2]:=1, X[1,2]:=4-1=3, N[2]:=6+3=9;

j=3: B[1,3]:=1, X[1,3]:=4-1=3, N[2]:=9+3=12.

j=4, тогда присваиваем NG:=17 и переход на шаг 15.

11) Вершины на второй окружности расположим еще 12 вершин: s[2,0]=1, s[2,1]=6, s[2,2]=7, …, s[2,10]=15, s[2,11]=16.

12) Ребра: каждую вершину первого яруса соединяем с тремя вершинами второго яруса, доводя степени вершин первого яруса до четырёх (рисунок 5.3.20а):

j=0: X[1,0]=3: (s[1,0]; s[2,0]), (s[1,0]; s[2,1]),

j=1: X[1,1]=3: (s[1,1]; s[2,3]), (s[1,1]; s[2,4]),

j=2: X[1,2]=3: (s[1,2]; s[2,6]), (s[1,2]; s[2,7]),

j=3: X[1,3]=3: (s[1,3]; s[2,9]), (s[1,3]; s[2,10]),

(s[1,0]; s[2,2]);

(s[1,1]; s[2,5]);

(s[1,2]; s[2,8]);

(s[1,3]; s[2,11]).

13) При слиянии вершин:

(s[2,0]; s[2,1]) – длина простого цикла = 4 < g=5;

(s[2,1]; s[2,2]) – длина простого цикла = 4 < g=5;

………………………………………………...

(s[2,11]; s[2,0]) – длина простого цикла =4 < g=5.

Граф остается без изменений

14) Введем поочередно ребра между соседними вершинами. Простой цикл длины пять получился при ребрах: (s[2,2]; s[2,3]), (s[2,5]; s[2,6]), (s[2,8]; s[2,9]), (s[2,11]; s[2,0]). Эти ребра добавляем в граф ( рисунок 1.3.20-б). Переход на шаг 6.

а)

б)

Рисунок 1.3.20. Фрагменты строящегося графа L(4,5)

6) i=2 < 3, переход на шаг 7.

7) i:=3 (третий ярус); j:=0; N[3]:=0.

8, 9, 10) j=0: B[2,0]:=2, X[2,0]:= 2, N[2]:=0+2=2;

j=1: B[2,1]:=1, X[2,1]:= 3, N[2]:=5;

j=2: B[2,2]:=2, X[2,2]:= 2, N[2]:=7;

j=3: B[2,3]:=2, X[2,3]:= 2, N[2]:=9;

j=4: B[2,0]:=1, X[2,4]:= 3, N[2]:=12;

j=5: B[2,5]:=2, X[2,1]:= 2, N[2]:=14;

j=6: B[2,6]:=2, X[2,2]:= 2, N[2]:=16;

j=7: B[2,7]:=1, X[2,3]:= 3, N[2]:=19;

j=8: B[2,8]:=2, X[2,8]:= 2, N[2]:=21;

j=9: B[2,9]:=2, X[2,9]:= 2, N[2]:=23;

j=10: B[2,10]:=1, X[2,10]:= 3, N[2]:=26;

j=11: B[2,11]:=2, X[2,11]:= 2, N[2]:=28.

j=12, тогда присваиваем NG:=45 и переход на шаг 11.

11) На третьей окружности: расположим еще 28 вершин: s[3,0]=17, s[3,1]=18, s[3,2]=19, …, s[3,26]=43, s[3,27]=44.

12) Каждую вершину второго яруса соединяем с вершинами третьего яруса, доводя степени вершин второго яруса до четырёх:

j=0: X[2,0]=3: (s[2,0]; s[3,0]), (s[2,0]; s[3,1]);

j=1: X[2,1]=3: (s[2,1]; s[3,2]), (s[2,1]; s[3,3]);

(s[2,1]; s[3,4]);

j=2: X[2,2]=3: (s[2,2]; s[3,5]), (s[2,2]; s[3,6]);

j=3: X[2,3]=3: (s[2,3]; s[3,7]), (s[2,3]; s[3,8]);

j=4: X[2,4]=3: (s[2,4]; s[3,9]), (s[2,4]; s[3,10]);

(s[2,4]; s[3,11]);

j=5: X[2,5]=3: (s[2,5]; s[3,12]), (s[2,5]; s[3,13]);

j=6: X[2,6]=3: (s[2,6]; s[3,14]), (s[2,6]; s[3,15]);

j=7: X[2,7]=3: (s[2,7]; s[3,16]), (s[2,7]; s[3,17]);

(s[2,7]; s[3,18]);

j=8: X[2,8]=3: (s[2,8]; s[3,19]), (s[2,8]; s[3,20]);

j=9: X[2,9]=3: (s[2,9]; s[3,21]), (s[2,9]; s[3,22]);

j=10: X[2,10]=3: (s[2,10]; s[3,23]), (s[2,10]; s[3,24]);

(s[2,10]; s[3,25]);

j=11: X[2,11]=3: (s[2,11]; s[3,26]), (s[2,11]; s[3,27]).

13) При слиянии вершин:

(s[3,0]; s[3,1]) – длина простого цикла = 0 < g=5;

(s[3,1]; s[3,2]) – длина простого цикла = 4 < g=5;

...

(s[3,27]; s[3,0]) – длина простого цикла =3 < g=5.

Все получаемые простые циклы имеют длину 0, 4 или 3. Поэтому граф остается без изменений.

14. Введем поочередно ребра между соседними вершинами. Простой цикл длины 5 получился при ребрах: (s[3,1]; s[3,2]), (s[3,4]; s[3,5]), (s[3,8]; s[3,9]), (s[3,11]; s[3,12]), (s[3,15]; s[3,16]), (s[3,18]; s[3,19]), (s[3,22]; s[3,23]), (s[3,25]; s[3,26]). Эти ребра добавляем в граф. Они показаны жирными линиями на рисунке 1.3.21. Переход на шаг 6.

6) i=3, т.е требуемое количество ярусов построено. Переход на шаг 15.

15) Конец алгоритма.

Рисунок 1.3.21. Планарный граф L(4,5) в трех ярусах

В результате построены первые три яруса бесконечного планарного графа L(4,5) (рисунок 1.3.19).

Пример 2. Рассмотрим теперь построение трёх ярусов бесконечного планарного графа L(3,4).

Исходные данные: v=3; g=4; NY=3.

Краткие выкладки по построению графа:

N[0]:=1; i:=1; N[1]:=3.

Начальная вершина s[0,0] соединяется ребрами с тремя вершинами первого яруса.

i:=2; j=0, ..., 2:

B[1,0]:=1; B[1,1]:=1; B[1,2]:=1;

X[1,0]:=2; X[1,1]:=2; X[1,2]:=2;

N[2]:=6. Строится шесть вершин на втором ярусе.

Фрагмент графа представлен на рисунке 5.3.22а.

Здесь при слиянии последовательно вершин (2,1)-(2,2), (2,3)-(2,4) и (2,5), (2,6) образуются простые циклы длины g1=4=g. N[2]:=3. Граф после слияния вершин и их перенумерации показан на рисунке 1.3.22б.

а) б)

Рисунок 1.3.22. Фрагменты строящегося графа L(3,4)

i:=3; j=0..2: B[2,0]:=2; B[2,1]:=2; B[2,2]:=2;

X[2,0]:=1; X[2,1]:=1; X[2,2]:=1; N[3]:=3.

Строятся три вершины на третьем ярусе. Вершины второго яруса соединяются ребрами с вершинами третьего яруса. Фрагмент графа представлен на рисунке 1.3.23а. Здесь все вершины третьего яруса слились в одну с образованием двух простых циклов длины пять – рисунок 1.3.23б.

а) б)

Рисунок 1.3.23. Планарный граф L(3,4) в трех ярусах

Ввиду сложности построения требуемого графа Л(N,v,g), который ищется методом перебора среди множества создаваемых графов Л(N,v,g), генерируется справочник заинтересованным производителем ВС, в котором наиболее часто используемые графы представлены в виде матриц смежности. Пример матрицы смежности графа Л(32,4,6) с d=4 и d_ср=2.36 представлен на рисунке 1.3.22.

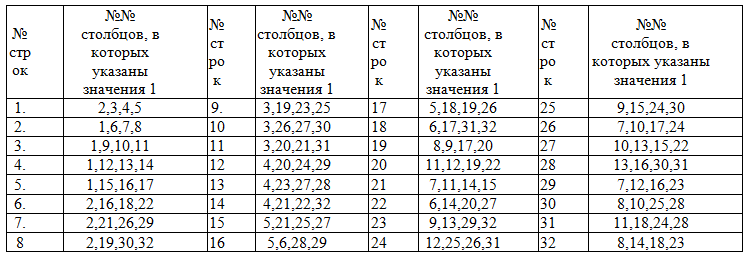
Рисунок 1.3.24. Матрица смежности для графа Л(32,4,6)

Определение 1.3.17. Структура вычислительной системы типа « Л(N,v,g) граф» описывается графом GS =(М, S*), где М – множество вычислительных модулей, определяемых вершинами графа, М ={mi}, i = 0, … , N-1. Связи сети S* соответствуют рёбра графа Л(N,v,g).

На рисунке 1.3.24 представлена структурная схема вычислительной системы МИКРОС (есть конфигурации МИКРОС-1, МИКРОС-2 и МИКРОС-Т), созданная на базе оптимальной сети, представленной графом D2(24, 3, 4). Каждый элемент В_i i=0, … ,23 представляет композицию из локальных коммутаторов и вычислительной части.

Рисунок1.3.24. Структура ВС МИКРОС в виде D2(24,3,4) графа

Рисунок 1.3.25. Структура элемента Bi вычислительной системы МИКРОС-Т

На рисунке 1.3.25 в состав элемента B_i входят транспьютер, коммуникационная память, процессор и оперативная память. Эта структура позволяет управлять переключением узлов с помощью программ и решать вычислительные задачи. Эта способность и порождает системы с программируемой структурой, а наличие процессора и оперативной памяти позволяет организовать вычислительный узел. Такая структура порождает настраиваемую под класс задач вычислительную сеть. В более простых случаях вместо транспьютера используется распределённый коммутатор и таким образом может быть создана вычислительная сеть или с фиксированной, или с программируемой архитектурой.