
лекции, учебные пособия / учебное пособие компьютерные лабораторные работы по динамике. мельников в. г., иванов с.е., мельников г. и. / pri_meh_method_complabrabpodin
.pdf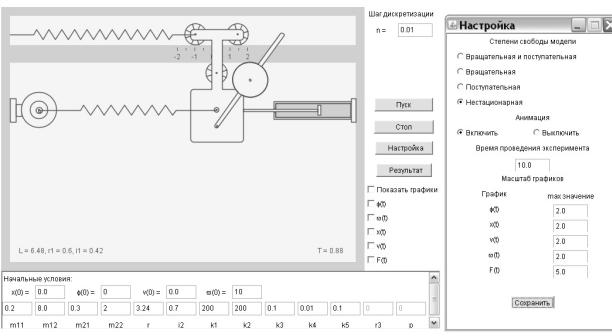
ЛАБОРАТОРНАЯ РАБОТА №5
КОЛЕБАНИЯ ГОЛОНОМНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
Исследуются линейные вынужденные колебания одностепенной голономной нестационарной системы, плоского механизма с пятью подвижными звеньями с одной нестационарной связью в виде заданного кинематического уравнения вращения маятника ϕ =ω0t
Цели работы
1.Экспериментальное определение амплитудно-частотной характеристики нестационарной механической системы с одной степенью свободы.
2.Сравнение экспериментальных результатов с результатами полученными по аналитическим формулам для нестационарной механической системы.
1.Описание установки
Рис. 5.1. Виртуальная лабораторная установка в нестационарном режиме
Перед выполнением работы необходимо в окне «Настройка» лабораторной установки переключить ее в режим «Нестационарная» (рис. 5.1).
На рис. 5.2. приведена схема установки. Она состоит из пружин жесткостью k1 и k2 .
61
Платформа состоит из груза массой m12 , который вместе с двухэлементным маятником массой m21 + m22 совершает возвратно-
поступательные движение по направляющей на четырех роликах массой
3m11 .
Маятник вращается с постоянной угловой скоростью ω =ω0 =ω(0) = const . Все три ролика платформа идентичны. Коэффициент
вязкого трения в подшипнике, радиус инерции и радиус каждого из роликов платформы обозначены соответственно символами k5 , i1 , r1 .
Масса пружин жесткостью k1 и k2 считается пренебрежимо малой. Демпфирующее устройство с коэффициентом вязкого трения k3 прикреплено справа к платформе.
Параметры механической системы:
•m11,m12 ,m21,m22 −массы соответствующих звеньев, остальные звенья установки считаются невесомыми
•k1,k2 −жесткость пружин
•k4 , k5 − коэффициенты вязкого трения в подшипниках
•k3 − коэффициент вязкого трения в демпфере,
•i2 −радиус инерции диска маятника,
•r −расстояние от оси подвеса маятника до центра диска массой
•x(0), x&(0) начальное состояние механической системы
Неизменяемые параметры механической системы:
•r1 ,i1 − радиус и радиус инерции колес платформы, их значения фиксированы и составляют r1 = 0.6 , i1 = 0.424
•l −длина стержня маятника, звено является однородным тонким стержнем, значение параметра фиксировано и равно l = 6.48
62

Рис. 5.2. Система с заданной нестационарной связью ϕ =ω0t
2.Математическая модель
Вкачестве обобщенной координаты и обобщенной скорости
механической системы выберем координату x |
и скорость v = x |
платформы. |
& |
|
Кинетическая энергия механической системы равна сумме кинетических энергий всех подвижных звеньев – трех колес, платформы и маятника.
|
3 |
|
|
i2 |
|
2 |
|
1 |
|
2 |
|
1 |
(m21 + m22 )v |
2 |
+ω0 cosω0t (m21l / 2 |
+ m22r )v |
|
T = |
|
m11 1 |
+ |
1 |
v |
|
+ |
|
m12v |
|
+ |
|
|
(5.1) |
|||
2 |
2 |
|
2 |
|
2 |
|
|||||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Виртуальная мощность системы приложенных сил вычисляется при условии ϕ = const . т.е. в предположении. Что с произвольного момента t маятник перестает вращаться.
Тогда маятник движется поступательно с момента времени t , равны нулю мощности сил тяжести маятника, мощности крутящего момента и момента трения в подшипнике. Получаем: P =F1 v +F2 v +F3 v +3M1тр щ
Обобщенная сила системы сил, приложенных к механизму |
|
Q = −(k3 + k4 )v −(k1 + k2 )x |
(5.2) |
Подставим выражения (5.1) и (5.2) в уравнение Лагранжа
63

|
d ∂T |
|
− |
∂T |
−Q = 0 |
|
|
|
|
|
∂x |
||
|
|
|||||
|
dt ∂v |
|
|
|
||
Получим дифференциальное уравнение движения нестационарной |
||||||
системы с одной степенью свободы: |
|
|
|
|
||
|
|
&& |
|
|
|
|
|
& |
|
|
|
|
|
2 |
sinω0t |
|
(5.3) |
|||
a11x + (k3 |
+ k4 )x |
+ (k1 + k2 )x = a12ω0 |
|
|||||||||||||||||
при обозначениях a |
= m + m |
|
+ m + |
9 m , |
a |
= m l / 2 + m r, |
|
|||||||||||||
11 |
12 |
|
|
21 |
|
22 |
2 |
11 |
12 |
21 |
|
|
22 |
|
||||||
Запишем уравнение движение в классическом виде: |
|
|
|
|
||||||||||||||||
|
|
&& |
+ |
|
& |
2 |
|
|
|
|
|
|
|
|
|
|
(5.4) |
|||
при обозначениях констант |
x |
2nx + k0 x = hsin(ω0t) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
n = |
k3 + k4 |
, |
|
k |
0 |
= |
k1 + k2 , |
h = |
a12 |
ω |
2 = a |
H |
ω 2 , |
(5.5) |
||||||
|
|
|
||||||||||||||||||
|
2a11 |
|
|
|
|
|
a11 |
|
|
|
a11 |
|
|
|
|
|
||||
где n- коэффициент демпфирования, k0 - собственная частота колебаний.
Предполагается, что характеристическое уравнение, составленное для дифференциального уравнения (5.4), имеет пару комплексно-сопряженных корней с малой вещественной частью.
Общее решение уравнения (5.4) состоит из частного периодического решения, и общего решения однородного уравнения с двумя константами
С и β :
|
x = H sin(ω0t −α) +Ce−nt sin(kt − β), |
|
k = |
k0 |
2 − n2 |
(5.6) |
||||||
H = |
|
h |
|
, α = arccos |
H (k2 |
−ω |
2 ) |
|
|
|
||
|
|
|
|
|
|
|||||||
|
(k02 −ω02 )2 + 4n2ω02 |
|
|
|
h |
0 |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Константы |
С и β |
определяются |
через |
начальные |
условия |
|||||||
x(0) = x0 , x&(0) = v0 посредством подстановки их в общее решение (5.6) и в
производную от него.
Согласно уравнению (5.6) система совершает двухчастотные колебания с собственной циклической частотой k и вынужденной частотой ω0 . При этом амплитуда собственных колебаний уменьшается по
показательному закону e−nt с коэффициентом затухания n , обусловленным трением.
В результате любое движение системы асимптотически приближается к одночастотному колебанию, не зависящему от начальных
условий, подчиненному уравнению: |
|
x = H sin(ω0t −α) |
(5.7) |
Система совершает гармонические колебания согласно формуле (5.7), асимптотически устойчивые относительно начальных возмущений.
Переходный процесс, начинающийся из любого состоянияx(0) = x0 , x&(0) = v0 , асимптотически переходит в периодические
колебания с постоянной амплитудой H , с частотой, равной частоте возмущающей силы и с фазой, смещенной на величину α .
64
3.Порядок выполнения работы
1.Задать постоянную угловую скорость ω0 =ω(0) = const , выбрать масштаб получаемых графиков.
2.Получить график x(t) колебаний. По графику определить период колебаний и максимальную амплитуду.
3.Вычислить амплитуду колебаний H по формуле (5.8) и смещение фазы α
4. Задать начальные условия x0 |
= −H sin(α) и x0 = −ω0 H cos(α) , |
|
& |
получить график x(t) колебаний. |
|
5.Сравнить эти графики с точным решением (5.7) нестационарной механической системы с одной степенью свободы, определить погрешность.
4. Содержание отчёта
1. График x(t) для ω0 =ω(0) = const . Период колебаний и максимальную амплитуду.
2.Амплитуду колебаний H и смещение фазы α .
3.График x(t) для x0 = −H sin(α) и x&0 = −ω0 H cos(α) , погрешность линеаризации.
65
Приложение А
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Виртуальная лабораторная установка (механическая система) представляет собой механизм с пятью подвижными звеньями: Т-образной подпружиненной платформы с тремя колесами и с маятником регулируемой длинны.
Электродвигатель обеспечивает через пружину “подкачку” энергии в систему, а линейный вязкий демпфер осуществляет диссипацию (тепловое рассеивание энергии).
Виртуальная лабораторная установка предназначена для изучения динамики стационарных и нестационарных механических систем с одной и двумя степенями свободы.
Для её работы необходимо, чтобы на компьютере был установлен
Internet Explorer 6.0 и установлена Java Runtime Environment 5.0,
последнюю версию которой можно бесплатно загрузить с сайта Sun Microsystems www.java.com/en/download/.
Виртуальная лабораторная установка разработана на языке программирования Java.
Пользовательский интерфейс виртуальной лабораторной установки показан на Рис.1. Он состоит из главного окна анимации и двух областей задания параметров и управления анимацией, расположенных внизу и справа от окна анимации.
В нижней области задаются параметры механической системы, а также – её начальные условия ν(0) ,ω(0) , x(0) ,ϕ(0) . Совокупность четырех
параметров V =[ν,ω, x,ϕ] называют фазовым вектором или вектором состояния системы в момент времени, а каждый из четырёх элементов называются фазовой координатой.
Вывод расчетных формул всегда происходит на основании рисунка, на котором показано “положительное” состояние объекта с положительными фазовыми координатами.
Справа от окна анимации расположено поле ввода параметра n , кнопка запуска и остановки анимации, кнопка настройки анимации «Настройка», кнопка вывода числовых результатов анимации «Результат».
66

Рис.А.1. Лабораторная установка
Параметры и начальные условия моделируемой модели механической системы задаются в соответствующих полях ввода.
К изменяемым параметрам лабораторной установки относятся: m11,m12 ,m21,m22 −массы соответствующих звеньев,
k1,k2 − коэффициенты жесткости пружин,
k3 − коэффициент вязкого трения в демпфере,
k4 − коэффициент вязкого трения в подшипниках трех колес, k5 − коэффициент вязкого трения в подшипниках маятника, i2 −радиус инерции диска маятника,
r3 −радиус эксцентрика электродвигателя,
r −расстояние от оси подвеса маятника до центра диска массой
В левом нижнем углу окна анимации отображены неизменяемые параметры лабораторной установки:
r1 = 0.6 , i1 = 0.424 - радиус и радиус инерции колес платформы, l = 6.48 - длина однородного тонкого стержня маятника.
67

Параметр моделирования n - “шаг дискретизации”, влияет на скорость и погрешность моделирования механической системы.
Вокне настройки анимации (рис.2) пользователь может выбрать степени свободы лабораторной установки: вращательная, поступательная, стационарная выбрав соответствующую кнопку.
Вокне настройки возможно отключить анимацию, которая по умолчанию включена.
Пользователь может установить время проведения эксперимента и масштаб получаемых в результате графиков.
Для того чтобы измененные параметры были применены, необходимо сохранить настройки, нажав соответствующую кнопку “Сохранить”
Рис.А.2. Окно настройки |
Рис.А.3 Окно результатов эксперимента. |
анимации. |
|
По окончании времени эксперимента пользователь при нажатии кнопки результат (рис.3) получает таблицу с исследуемыми параметрами с заданным шагом по времени.
Для получения необходимых графиков эксперимента x(t) , ϕ(t) , ν(t) , ω(t) , F(t) (рис.4) пользователь может выбрать соответствующие кнопки или выбрать все графики отметив кнопку “Показать графики”.
68

Рис.А.4. Графики результатов эксперимента
69
ЛИТЕРАТУРА
1.Мельников В.Г., Иванов С.Е., Мельников Г.И. Компьютерные технологии в механике приборных систем. Учебное пособие / Под редакцией В.Г. Мельникова. – СПб: СПб ГУ ИТМО, 2006. – 127 с.
2.Кривошеев А.Г., Мельников Г.И., Тихонов А.А. Под. ред. Г.И. Мельникова. Статика на компьютере. – СПб., ГИТМО(ТУ) 2000.
3.Курс теоретической механики. / Дронг В.И., Дубинин В.В., Ильин М.М. и др. Под ред. К.С. Колесникова. – М.: МГТУ им Н.Э. Баумана, 2005.
4.Тарг С.М. Краткий курс теоретической механики. – М.: Наука, 2005
5.Диевский В.А. Теоретическая механика. – СПб.: изд. Лань, 2005. – 320 с.
6.Яблонский А.А., Никифорова В.Я. Курс теоретической механики.
М.:Наука, 2001
7.В.М. Сурин Прикладная механика – Минск: ООО " Новое знание", 2006 . – 388 с
8.Маркеев А.П. Теоретическая механика. – М.:Наука, 2001.
9.Журавлев В.Ф. Основы теоретической механики. – М.: Наука, 2001.
10.Тимошенко С.П. Колебания в инженерном деле. – М.:Наука, 1967. – 444 с.
70
