лекции, учебные пособия / учебное пособие компьютерные лабораторные работы по динамике. мельников в. г., иванов с.е., мельников г. и. / pri_meh_method_complabrabpodin

Рис. 2.2. Маятник двухстепенной системы

Мощность пар сил вязкого трения в подшипниках колес

M11тр щ11 =−3k4ω112 cos(щ11,щ11) =−3k4ω112

где принято во внимание, что момент M11тр направлен перпендикулярно плоскости рисунка, а щ11 “от нас”.

В выражении (2.3) для мощности Pм(1) следует учитывать, что маятник зафиксирован поэтому угол между силами G21, G22 и скоростями точек их приложения vG21, vG22 остается постоянным и равным π / 2 . Во

всех механических системах мощность сил и моментов вязкого трения отрицательна, т.е. PMтр ≤0, PFтр ≤0 .

Кинематическое состояние механизма V =[v, x], при котором его

обобщенные скорости и обобщенные координаты имеют положительные значения [v > 0, x > 0] , соответствует положительному фазовому вектору V и называется положительной фазой. На рис. 2.2. представлен механизм, находящийся в положительной фазе. В общем случае в процессе движения элементы фазового вектора могут принимать как положительные, так и отрицательные значения, но расчетные формулы получены для положительной фазы.

Обобщенная сила одностепенной системы находится по формуле

41

1.2. Механизм с двумя степенями свободы

1.2.1. Описание двухстепенного механизма

Механическая система с отклоненным маятником, совершающая угловые колебательные движения на подвижной платформе (рис.2.3.) состоит из поступательно движущейся со скоростью v платформы на которой вращается тела вокруг осей. В таком случае механизм имеет две степени свободы, представляет собой голономную стационарную двухстепенную механическую систему. Положение такой системы фиксируется двумя обобщенными координатами q1,q2 , в качестве которых

примем направленную линейную координату x и направленную против часовой стрелки угловую координату ϕ . Быстрота движения характеризуется двумя соответствующими обобщенными скоростями q&1 = v, q&2 =ω.

Фазовый вектор состояния двухстепенной системы содержит четыре фазовые координаты характеризующие быстроту и конфигурацию объекта

выводе расчетных формул положительную фазу движения, а затем – фазу в соответствии с заданием.

Мощность системы приложенных сил состоит из мощности сил на поступательном движении и мощности моментов сил взятых относительно осей вращения на угловых скоростях относительного вращения. Две обобщенные силы находятся путем приведения подобных членов в мощности, выделения коэффициентов при v,ω. При этом зависимости сил

и моментов от v,ω следует раскрывать лишь после выполнения группировки членов. Кинетическая энергия системы равна кинетической энергии поступательного движения вместе с поступательной системой отсчета сложенной с кинетической энергией вращения звеньев вокруг своих осей и дополнительных членов для неуравновешенных звеньев, в данном случае для маятника.

42

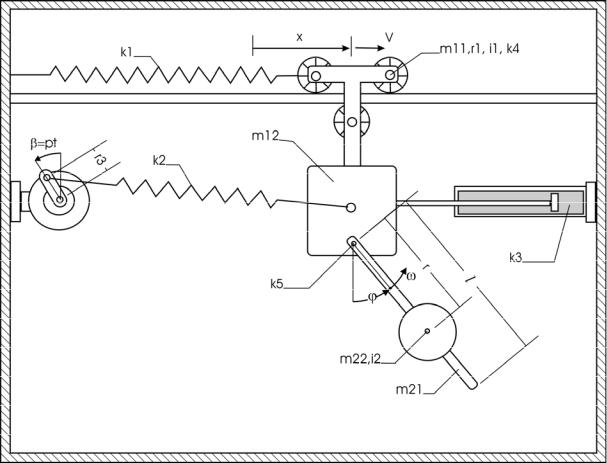
Рис. 2.3. Механизм с двумя степенями свободы

1.2.2. Мощность и обобщенные силы

В качестве двух обобщенных координат механической системы выберем направленную вправо линейную координату x платформы и направленную против часовой стрелки угловую координату ϕ маятника.

нас.

Силы тяжести всех звеньев на поступательном движении не имеют мощностей ввиду их перпендикулярности к скорости v , поэтому их опускаем в формулах, имеет мощность (отрицательную) только сила сопротивления демпфера F3 и две упругие силы F1,F2 . На вращательном относительном движении имеют мощность моменты сил тяжести неуравновешенного маятника M21,M22 и моменты трения в подшипниках 3M4,M5 , направленные противоположно угловым скоростям и поэтому имеют отрицательные мощности.

Получаем выражения мощностей всей системы сил и пар сил, приложенных к устройству, показанному на рисунке.

43

P = (F1 + F2 + F3 ) v +3M4 ω1 + (M5 + M21 + M22 ) ω

или, выражая скалярные произведения через произведения проекций сомножителей:

P = (F1X + F2 X + F3 X )v −3M4v / r1 + (−M5 + M21 + M22 )ω

где M4 , M5 - модули моментов трения, M21, M22 - моменты сил тяжести маятника относительно оси О, отрицательные для показанного на рис.2.3

Коэффициенты в мощности при обобщенных скоростях называются обобщенными силами. Получаем обобщенные силы по обобщенной скорости v и по угловой скорости ω:

Q1 = −3M4 / r1 + F1X + F2 X + F3 X

Q2 = −M5 + M21 + M22

На данном этапе можно раскрывать функциональную зависимость обобщенных сил от фазовых координат и времени.

Окончательно получаем выражение

Расчетная формула мощности системы приложенных сил в произвольной фазе движения, в произвольный момент времени:

где функции Q1 ,Q2 определяется формулой (2.6)

Замечание. Пусть к физическому маятнику дополнительно приложен

некоторый крутящий момент M kp , создаваемый дополнительным двигателем, расположенным на платформе около оси О. Тогда, очевидно, этот момент войдет в виде слагаемого в формулу (2.6).

Линеаризацией выражений называется приближение (аппроксимация) нелинейных функций от фазовых координат на малом интервале изменения этих координат. В данном случае, предполагается, что при малых колебаниях маятника, например в пределах −π / 10 ≤ϕ ≤π / 10 можно в формуле (2.6) положить sin(ϕ) =ϕ , т.е. спрямить нелинейную

Выражение для первой обобщенной силы есть линейная функция относительно фазовых переменных v, x , поэтому остается неизменным. Очевидно, что коэффициент М равен модулю момента сил тяжести маятника при его отклонении от вертикали на угол π / 2.

44

2. Порядок выполнения работы.

1.1.В соответствии с номером варианта и таблицы 2.1. ввести значения параметров и начальные условия одностепенной механической системы. В окне «Настройки» задать режим «одностепенная» Произвести моделирование движения механизма, получить графики x(t), v(t) , F(t) .

1.2.По графикам v(t) , x(t), определить численное значение фазового вектора V =[v, x] одностепенной системы для заданного момента

времени t1 . Изобразить механизм в состоянии, соответствующем

значению фазового вектора.

1.3.Вычислить мощности внешних сил приложенных к платформе:

3.Содержание отчёта

Вотчёт о проделанной лабораторной работе должны быть включены следующие разделы:

1.Номер варианта и исходные данные для расчёта.

2.Графики x(t), v(t) , F(t) , одностепенной системы, численное

значение фазового вектора V =[v, x] для заданного момента

времени t1 . Изобразить механизм в состоянии, соответствующем значению фазового вектора.

3. Мощности внешних сил приложенных к платформе: P3G11 , PF1 ,

PMтр , PG12 , PFтр , PF и Pпл(1) .

4.Мощности сил, приложенных к маятнику: PG 21 , PG 22 , и мощность P1м системы сил.

5.Мощность P(1) системы сил, приложенной к одностепенной системе и обобщенная сила Q(1) одностепенного механизма

6.Графики x(t), ϕ(t), v(t) ,ω(t) , F(t) двухстепенной системы.

7.Фазовый вектор двухстепенной системы V =[v,ω, x,ϕ] для

заданного момента времени t1 . Изобразить механизм в состоянии, соответствующем значению двухстепенного фазового вектора.

45

8. Мощности системы сил Pм(2) , Pпл(2) и мощность системы сил, приложенной к двухстепенной системе.

9.Две обобщенные силы Q1(2) и Q2(2)

4.Исходные данные для выполнения лабораторной работы.

Таблица 2.1.

46

ЛАБОРАТОРНАЯ РАБОТА №3

СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ ЛИНЕЙНОЙ И НЕЛИНЕЙНОЙ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ

В работе исследуются свободные затухающие колебания системы с одной степенью свободы на примере колебаний физического маятника. Определяется частота собственных колебаний, логарифмический декремент колебаний, коэффициент вязкого трения и коэффициент демпфирования. Оценивается влияние на период колебаний погрешности линеаризации уравнений, выполненной двумя способами. Линейными колебаниями называют повторяющиеся движения, подчиненные линейным дифференциальным уравнениям, нелинейными – в том случае если ОДУ содержат хотя бы один нелинейный член относительно переменных состояния. Переход от нелинейной математической модели к линейной обычно осуществляется линеаризацией нелинейных параметров.

Цель работы

Экспериментальное определение периода собственных колебаний и определение логарифмического декремента колебаний. Оценка погрешности линеаризации.

1. Описание установки.

Рис. 3.1 Лабораторная установка

47

Кинетическая энергия T системы состоит из кинетической энергии маятника и кинетической энергии груза. Она приводится к виду T = 12 a22ω2

, посредством вынесения общего множителя ω2 / 2 , где полученный коэффициент a22 называется приведенный коэффициент инерции

механизма

Коэффициент (3.1) называется также приведенным моментом инерции маятника. В данном случае a22 есть момент инерции физического

маятника относительно оси подвеса Oz , состоящего из двух тел. Обобщенная сила Q , определяется как частное от деления мощности

P системы сил на угловую скорость, Q = P /ω , и представляет собой в

данном случае главный момент системы приложенных сил. Мощность системы сил состоит из мощностей сил тяжести и мощности момента пары сил трения:

P = (M21 + M22 + Mтр) щ или P = −((m21gl / 2 + m22 gr)sin(ϕ) −Mтр ) щ (3.2)

Либо мощность можно вычислить через мощность моментов сил:

После выполнения указанных в нем вычислений над кинетической энергией принимает форму дифференциального уравнения второго порядка

где начальное состояние механической системы [ω0 , ϕ0 ] должно быть

задано.

Для рассматриваемой механической системы ∂a22 / ∂ϕ = 0 , в виду того, что a22 = const и уравнение (3.3) имеет вид

обобщенной силы, в качестве которой и имеем главный момент приложенных сил.

49

Математическая модель механической системы (3.5)-(3.4) является нелинейной, ввиду нелинейной зависимости обобщенной силы Q от угла

поворота. Считаем, что эта модель является точной, она точно описывает движение маятника при больших и малых колебаниях, но при малых колебаниях функцию Q =Q2 будем определять по формуле (2.8).

При колебаниях с малой амплитудой удовлетворяющих, например

при M = m22 gr + m21gl / 2

Подставим линейную функцию (3.6)относительно фазовых переменных [ϕ&, ϕ] в уравнение и введем новые обозначения

коэффициентов. Получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами вида

Дифференциальное уравнение (3.7)-(3.8) вместе с начальными условиями (3.4) представляет собой математическую модель линейных колебаний маятника, называемую задачей Коши. Параметр n называется

коэффициентом затухания, параметр k0 - собственной циклической частотой незатухающих колебаний без трения. Наряду с параметром k0

будем рассматривать также параметр k вида

называемый собственной циклической частотой затухающих колебаний.

В уравнении (3.7) слагаемое 2nϕ& обусловлено наличием в механизме

Из выражения (3.10) следует, что система совершает гармонические колебания с затухающей амплитудой A = A0 e−nt , с начальной фазой α , с

50