лекции, учебные пособия / учебное пособие компьютерные лабораторные работы по динамике. мельников в. г., иванов с.е., мельников г. и. / pri_meh_method_complabrabpodin

Обобщенной силой нестационарной голономной одностепенной

механической системы называется отношение виртуальной мощности системы сил (мощности системы сил на виртуальных скоростях) к обобщенной скорости:

В общем случае Q есть функция трех параметров: Q =Q(q&, q,t). В (1.50) силы зависят от действительных (не виртуальных) скоростей. Уравнение Лагранжа для нестационарной одностепенной системы имеет такой же вид, как и для стационарной системы:

т.е. полная производная по времени от обобщенного импульса ∂T∂q&, уменьшенная на величину ∂T∂q равна обобщенной силе системы

приложенных сил, определяемой по формуле (1.50) через мощность реальных сил на виртуальных скоростях.

Выполнив процедуры дифференцирования трехчленного выражения кинетической энергии (1.48), указанные в уравнении (1.51), получим окончательно динамическое уравнение в форме ОДУ второго порядка вида:

Начальные условия не задают в случае, когда требуется найти установившийся периодический режим колебаний, тогда их заменяют требованием периодичности искомого частного решения.

21

Пример. Электродвигатель с вращающимся кривошипом.

Рис. 1 Вибрация подпружиненного электродвигателя с вращающимся кривошипом

Электродвигатель массой m1 , включающий массу корпуса, платформы

и четырех направляющих колес, установлен на пружинах общей жесткости с2 , с массой пружин m2 . Радиусы инерции каждого из четырех

направляющих колес i3 , радиусы колес r3 , масса колес m3 . На оси О двигателя установлен неуравновешенный маховик массой m4 с расстоянием до центра масс r4 , радиус инерции маховика относительно

оси О равен i4 , маховик равномерно вращается согласно кинематическому уравнению φ= ω4 t , при ω4=2. Задан общий момент вязкого трения на осях M3= b3 ω3 . Составить динамическое уравнение устройства.

Решение Уравнением ϕ= ω4t =2t задана нестационарная связь.

Пружины не создают связей, они лишь создают силы и имеют инерционность, которую согласно методу Рэлея учтем, прибавив к массе m1 двигателя третью часть массы пружин m2 . Имеем нестационарную

механическую систему с одной степенью свободы, в которой за обобщенную координату примем направленное вверх смещение от положения оси О, соответствующего недеформированному состоянию пружины.

22

G1 = −m1g j , G4 = −m4 g j

Кинетическая энергия устройства состоит из кинетической энергии его поступательного движения со скоростью v , вращения четырех колес вокруг их центров масс и энергии маховика со смещенным от оси центром масс:

где v vCO = −vω4r4 sin(ω4t) .

Отсюда получаем кинетическую энергию в форме квадратного полинома относительно v :

Обобщенная сила Q по обобщенной скорости v = y& находится через вычисление виртуальной мощности системы всех приложенных сил на виртуальных скоростях точек приложения сил. При этом в выражениях сил зависящих от скоростей не следует заменять действительные скорости на виртуальные. Не принимаем во внимание крутящий момент электродвигателя вместе с моментом трения в подшипнике O , осуществляющих нестационарную связь – программное движение кривошипа, поскольку их мощность на виртуальном движении при фиксированном в связях параметре t (т.е. при ϕ = const ) равна нулю.

Мощность силы G4 подсчитываем на виртуальной скорости vC* = v . Центр

масс пружин амортизатора имеет скорость v / 2 . Имеем:

Подставляя в уравнение Лагранжа (1.52) выражения (1.59),(1.60) получаем динамическое уравнение устройства:

23

Окончательно имеем линейное неоднородное ОДУ второго порядка с постоянно действующими периодическими возмущениями следующей

Общее решение уравнения (1.61) состоит из частного периодического решения, имеющего гармоническую и постоянную составляющие, и общего решения однородного уравнения с двумя константами С и β :

частотой k1 и вынужденной частотой p . При этом амплитуда собственных

колебаний уменьшатся по показательному закону e−nt с коэффициентом затухания n , обусловленным вязким трением. В результате любое движение системы асимптотически приближается к одночастотному колебанию, не зависящему от начальных условий, подчиненному уравнению:

Иными словами, система совершает гармонические колебания согласно формуле (1.64), асимптотически устойчивые относительно начальных возмущений в том смысле, что любой переходный процесс, начинающийся

постоянной амплитудой H , с частотой, равной частоте возмущающей силы и с фазой, смещенной на величину α от фазы кинематического возмущения.

Замечание В случае нестационарной одностепенной механической

уравнения T& = P получается дифференциальное уравнение, содержащее мощность крутящего момента. Такое уравнение можно использовать для

24

вычисления крутящего момента, обеспечивающего выполнение нестационарной связи, но прежде следует применить уравнение Лагранжа и получить решение (1.64).

Замечание Имеется другой способ решения одностепенной нестационарной задачи. Можно обобщенную координату q переобозначить q1 и в уравнении нестационарных связей время t переобозначить q2 , вводя

условно дополнительную координату, дополнительную степень свободы. Получаем стационарную двухстепенную механическую систему для которой составляем два уравнения Лагранжа. Затем в этих уравнениях полагаем q2 =t , первое из уравнений есть искомое ОДУ, второе можно

отбросить или использовать для реакций нестационарных связей. В рассмотренном примере в качестве q2 можно принять угол поворота кривошипа и в конце принять q2 =ω4t

25

ЛАБОРАТОРНАЯ РАБОТА №1

ОПРЕДЕЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МНОГОЗВЕННОГО МЕХАНИЗМА С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ

В работе определяется и исследуется кинетическая энергия механической системы с двумя степенями свободы, совершающей вынужденные колебания в условиях периодических возмущений создаваемых электроприводом при заданном начальном состоянии системы. Механизм представляет собой поступательно движущуюся платформу, на которой размещены три уравновешенных вращающихся колеса и физический маятник, состоящий из двух элементов с известными положениями центров масс.

Цель работы

Определение кинетической энергии многозвенного механизма с двумя степенями свободы по экспериментальным данным и расчетным формулам в виде однородной квадратичной формы относительно обобщенных скоростей с постоянными и зависимыми от обобщенных координат коэффициентами, и составление матрицы инерции механизма.

1. Описание установки

Рис.1.1. Окно виртуальной лабораторной установки

26

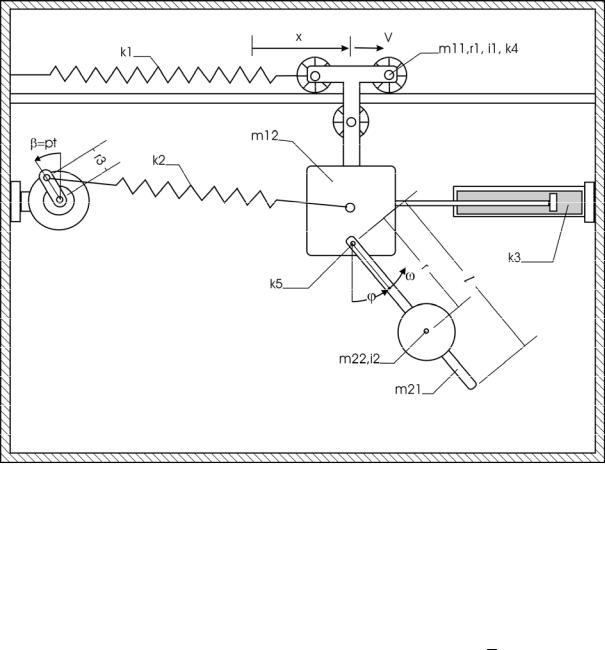
Рис. 1.2. Параметры системы с двумя степенями свободы

2. Математическая модель

Общая трехчленная формула для двойной кинетической энергии

плоского движения тела имеет вид

где vo - скорость полюса тела, OC - расстояние от полюса O до центра массы С,Oz – ось вращения, Joz - момент инерции тела относительно оси, проведенной через полюс перпендикулярно плоскости движения, vco -

относительная скорость вращения центра масс тела С вокруг полюса O .

vo vco =vo vcocos(vo vco )

В случае, когда за полюс принят центр масс тела, получаем из (1.1) двухчленную формулу:

28

Кинетическая энергия механической системы равна сумме кинетических энергий всех ее звеньев:

совершающего плоское движение

T22 - кинетическая энергия диска массой m22 , совершающего плоское

движение

T2 - кинетическая энергия маятника, состоящего из стержня и диска.

При обозначении (1.4), окончательная формула (1.3) принимает вид кинетической энергии механической системы:

2.1. Кинетическая энергия платформы и колес

Двойная кинетическая энергия платформы, движущейся поступательно определяется формулой

Кинетическая энергия трех колес с общей массой 3m11 , совершающих

плоское движение состоит из кинетической энергии поступательного движения вместе с полюсом О и кинетической энергии вращения вокруг О в поступательной системе отсчета

Коэффициент инерции системы трех колес, приведенный к скорости

a11 =3m11(1+i12 / r12 )

2.2.Кинетическая энергия маятника

В данном механизме маятник совершает плоское движение. Найдем его кинетическую энергию T2 двумя способами.

29

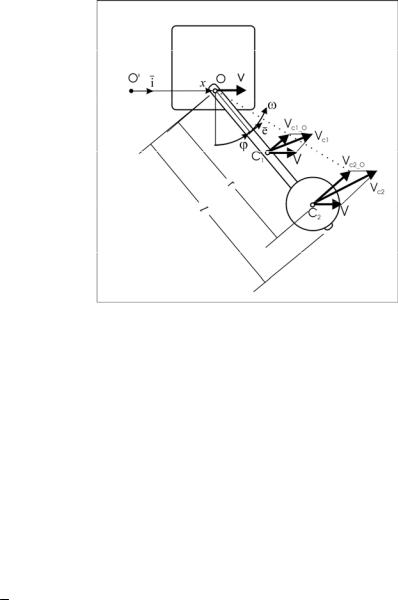
Первый способ

Из выражения (1.2) следует, что кинетическая энергия маятника (Рис.6) состоит из энергии стержня и диска, совершающих плоское движение, из четырех слагаемых,

их центральных осей, перпендикулярных плоскости движения.

Рис. 1.3. Маятник

Скорости центров масс находятся как векторные суммы скорости

полюса и относительной скорости движения вокруг полюса:

e OC1

(1.10)

Здесь i -орт линейной координаты x , e - сопровождающий касательный орт угловой координаты ϕ направленный против часовой стрелки, O -

точка подвеса маятника, v - скорость точки O , равная скорости платформы, vC1_ O и vC 2 _ O - относительные скорости вращения центров

масс стержня и диска маятника вокруг точки подвеса O , vC1_ O и vC 2 _ O -

30