Порядок выполнения работы
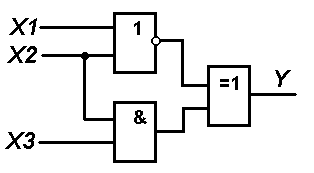
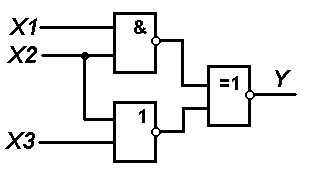
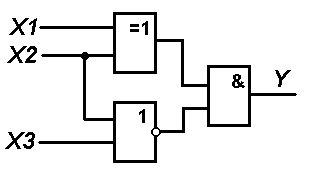
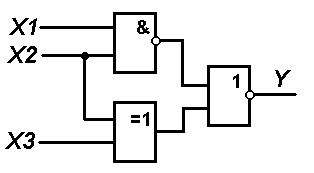
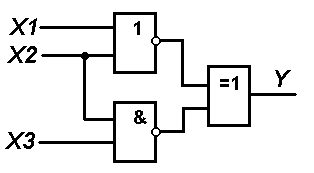
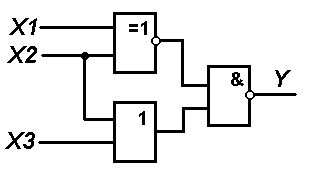
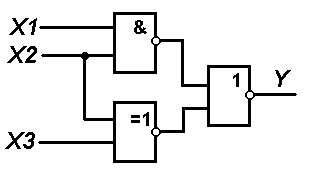
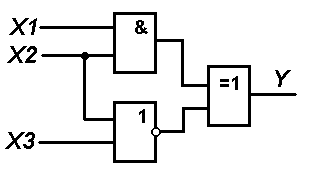
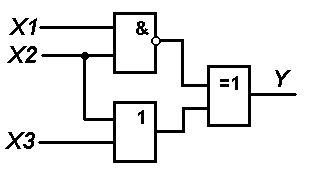
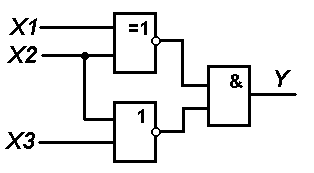
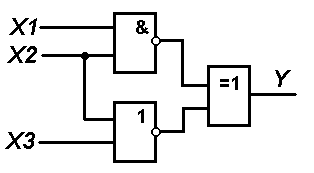
1. В соответствии с вариантом выбранного задания каждому студенту следует согласно схеме представленной на рисунке составить логическую функцию и таблицу истинности
Вариант №1 |
Вариант №2 |
Вариант №3 |
|
|
|
Вариант №4 |
Вариант №5 |
Вариант №6 |
|
|
|
Вариант №7 |
Вариант №8 |
Вариант №9 |
|
|
|
Вариант №10 |
Вариант №11 |
Вариант №12 |
|
|
|
2. В соответствии с вариантом выбранного задания каждому студенту следует согласно заданной булевой функции составить логическую схему устройства и таблицу истинности
Вариант |
Функция |
|
Вариант |
Функция |
1 |
|
|
10 |
|
2 |
|
|
11 |
|
3 |
|
|
12 |
|
4 |
|
|
13 |
|
5 |
|
|
14 |
|
6 |
|
|
15 |
|
7 |
|
|
16 |
|
8 |
|
|
17 |
|
9 |
|
|
18 |
|
Практическая работа №3 «Синтез логических схем в базисах имс»
Цель работы:
Оборудование: ПЭВМ
Программное обеспечение: Electronics Workbench
Основные положения Лабораторная работа №1 «Изучение работы дешифратора»
Цель работы: Изучить принцип работы дешифратора
Оборудование: ПЭВМ
Программное обеспечение: Electronics Workbench
Основные положения
Шифраторы и дешифраторы. Основными видами преобразования информации являются шифрование и дешифрование (сжатие данных и обратное преобразование). Для реализации таких преобразований служат шифраторы и дешифраторы. Они представляют собой комбинационные устройства, поскольку состоят только из логических элементов, а элементов памяти не имеют. Шифраторы преобразуют код «1 из N» в двоичный код, а дешифраторы – двоичный код в код «1 из N». Число разрядов двоичного кода обычно меньше N, поэтому операцию шифрования можно считать сжатием данных. Иными словами, шифратор превращает сигнал 1 на одном из нескольких входных зажимов в выходную кодовую комбинацию. Поэтому для шифратора используется также название «кодер», а на его условном обозначении пишут буквы CD. Дешифратор превращает комбинацию из нулей и единиц на входе в сигнал 1 только на одном единственном из нескольких выходных зажимов. Поэтому для дешифратора используется также название «декодер», а на его условном обозначении пишут DC.
Дешифраторы широко применяются в устройствах управления, вывода информации на цифровые индикаторы, в коммутаторах для распределения сигналов по различным цепям.
Различают полные и неполные дешифраторы. Число выходов у полного дешифратора Nвых = 2n, а у неполного Nвых < 2n, где п – число двоичных разрядов (число входов). На рис. 4.1, а приведено условное графическое обозначение полного стробируемого дешифратора «1 из 8», а табл. 4.1 представляет собой его таблицу истинности.
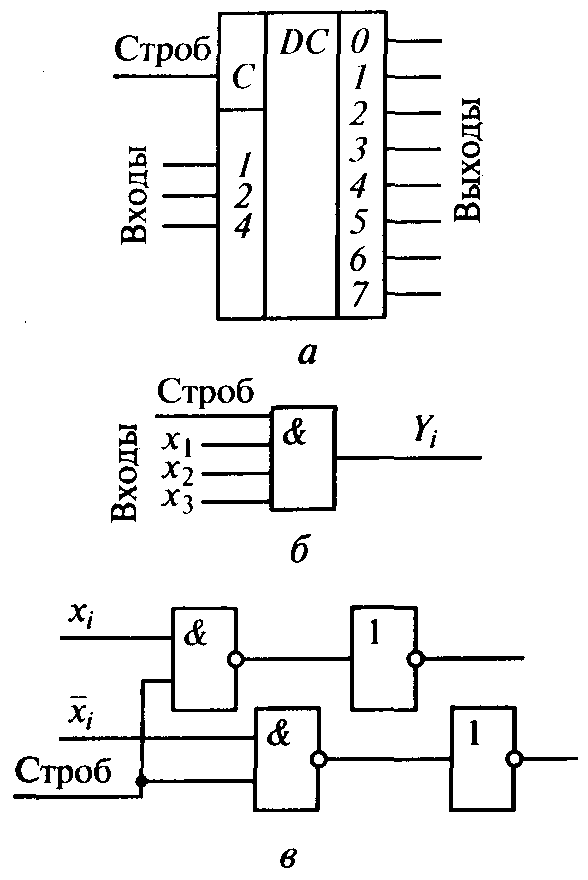
Рис. 4.1. Условно-графическое обозначение дешифратора «1 из 8»:
Шифратор – это комбинационное устройство, преобразующее код «1 из N» в двоичный код. Полный шифратор имеет 2n входов и п выходов. Одно из основных применений шифратора – ввод данных с клавиатуры, при котором нажатие на клавишу с десятичной цифрой должно приводить к передаче в устройство этой цифры в двоичном коде. При нажатии любой из десяти цифровых клавиш единица появляется только на одном из десяти входов шифратора X0, X1, ..., X9. На выходе шифратора должен появиться двоичный код (y0 y1 y2 y3) введенного десятичного числа. Из таблицы истинности (табл. 4.2) видно, что в этом случае нужен преобразователь с десятью входами и четырьмя выходами, т.е. так называемый шифратор «10 – 4».
Таблица 4.1
Таблица истинности дешифратора «1 из 8»
Входная кодовая комбинация |
Сигнал на выходе |
||||||||||
С |
x1 |
x2 |
x3 |
Y0 |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
Y6 |
Y7 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
Любые комбинации нулей и единиц |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
Таблица 4.2
Таблица истинности шифратора «10 – 4».
Десятичное число |
Сигнал на входе |
Выходная кодовая комбинация |
||||||||||||
Х0 |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
Х9 |
у3 |
у2 |
у1 |
у0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
На выходе у0 единица должна появиться при нажатии любой нечетной клавиши (Х1, Х3, Х5, Х7, Х9), т. е. у0 = Х1 v Х3 v Х5 v Х7 v X9. Состояние остальных выходов определяется следующими логическими функциями:
y1 = Х2 v Х3 v Х6 v Х7; у2 = Х4 v Х5 v Х6 v Х7; у3 = Х8 v X9.
Следовательно, для реализации указанного шифратора понадобятся четыре логических элемента ИЛИ: пятивходовый, два четырехвходовых и двухвходовый.