1. Синхронный метод

Множитель находится в едином регистре В, управление осуществляется одним УА, умножение производится одновременно на разряды n и n/2 множителя. Такт суммирования пропускается, если только разряды множителя n и n/2 равны 0, иначе сложение выполняется хотя бы на одном сумматоре. В такте сдвига УА вырабатывает сигнал микрооперации сдвига в обоих сумматорах и регистре В (обе части регистра В сдвигаются одновременно).

t_умн.ср=_.n/2(3/4Т_умн.+Т_сдв.)+Т_сум.

n n/2

0 0 - такт сложения пропускается

0 1

1 0

1 1

2. Асинхронный метод

Старшая и младшая часть множителя находится в двух разных регистрах В₁ и В₂: регистр В аппаратно разделен на две части, управление осуществляется двумя автономными УА. Первый УА управляет вычисление суммы частичных произведений при умножении на В₁, второй УА – на В₂. в одном и том же такте в каждом из сумматоров может хранится сумма 5 и 7 частичных произведений(3 и 6, и т.д.). Операции сдвига в В₁С₁ и В₂С₂ независимы и инициируются разными УА. По окончании процесса умножения выдается в каждом из сумматоров осведомительный сигнал.

t_умн.ср=_.n/2(0.5Т_умн.+Т_сдв.)+Т_сум.

Если сумматоров к, то t_умн.ср=_.n/к(0.5Т_умн.+Т_сдв.)+Т_сум.

Для предельного распараллеливания процесса требуется n-1 сумматоров, чтобы сложить n частичных произведений за 1 такт. Подобное устройство называется одновременным множительным устройством.

Использование сумматора с запоминанием переноса.

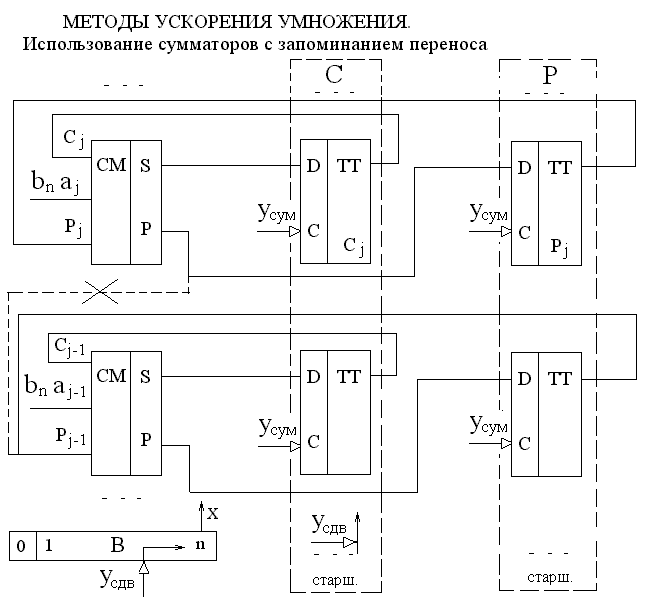
t_сум=nt_кс+t_{пр.кода}

Основная идея:

n-разрядный сумматор строится на базе одноразрядных сумматоров с разорванными цепями переноса. Переносы запоминать на регистре и прибавлять к сдвинутой сумме частичных произведений в следующем такте.

В цикле проверки B_n

1такт – y(+) (множитель+сумма част.произведений+перенос)

2Такт – y(-)(сдвиг)

Пропуски тактов суммирования в этом алгоритме запрещены, т.к. перенос всегда необходимо прибавлять.

После n циклов вычисленное произведение будет представлено двумя числами С и Р. их нужно сложить на обычном сумматоре с замкнутыми цепями переноса.

Пример:

В 0 0111 0 0111 0 1011 0 1011 0 0101 0 0101 0 0010 0 0010 0 1001

СМ 00 0000 00 1111 00 0111 00 1000 00 0100 00 1100 00 0110 00 0001 00 0000

Р 0000 0000 0000 0111 0111 0111 0111 0110 0110

А 0 1111 0 1111 0 1111 0 1111 0 1111 0 1111 0 1111 0 1111 0 1111

Сч 00 00 01 01 10 10 11 11 00

0 1001 7/16*15/16=105/256

00 0110 6/16+9/256=105/256

0110

0 1111

00

Дерево сумматора.

Идея: увеличить количество сумматоров с разорванными цепями переноса, чтобы умножение производилось за 1 такт.

С₁+С₂+С₃=S₁^s+S₂^p

C₁+C₂+…+C_n= 2/3n слагаемых

4/9n слагаемых и т.д.

Ускорение достигается за счет того, что при выработке каждой суммы в каждом из n-2 сумматоров нет задержки распространения переноса. Последние два слагаемых складываются на n-1 сумматоре, у которых цепи переноса замкнуты.

Если очередной ярус слагаемого не делится на 3 , свободные входы сумматоров можно использовать для прибавления суммы из другого яруса.

Дерево сумматора для умножения 12-разрядных чисел:

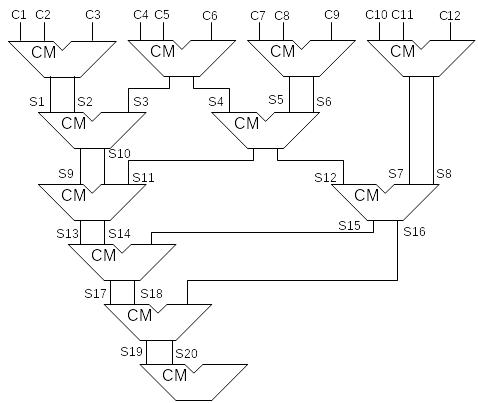
С_i(1:n)=A(1:n)*b_i

t_сум=17_кс<=24t_кс<=2nt_кс

Все слагаемые подаются на сумматоры с необходимым сдвигом.

Пример:

0,1111*0,1111

дерево сумматора:

t_сум=2t_кс+5t_кс=7t_кс

1					1	1	1	1	C1 Sum8
				1 1	1 1	1	1		C2 C2
			1	1	1	1			C3
			1	0	1	1	0		S1
			0	1	1	1	1		S2
2			1	0	1	1	0		S1 Sum7
		0	1	1	1	1			L1(S2)
		1 1	1 1	1 1	1				C4
		1	1	0	1	0			S3
		0	1	1	1	1			S4
3		1	1	0	1	0			S3 Sum6
	0	1	1	1	1				L1(S1)
	1	1	1	0	0				Sum(1:5)

Умножение чисел представленных в дополнительных кодах.

С=А*В

1. В>0

Алгоритм умножения применяется без изменения. К сумме частичных произведений в каждом такте прибавляется А, если цифра B_n =1. знаковые разряды С иа учавствуют в суммировании, у А знаковый разряд при суммировании удваивается.

С 11 0111

После сдвига 11 1011

С 10 1000

После сдвига 11 0100

2. B<0

А*(-В)=А*(1-В)=А-АВ

1-АВ

А-АВ+(1-А)=1-АВ

Корректирующее слагаемое

После умножения в цикле на n цифр множителя к сумматору прибавляется корректирующее слагаемое(кс). Если B>0, то корректирующее слагаемое=0, иначе – 1-А .

А*В

5*6 кс=0

-5*6 кс=0

5*(-6) кс=1-5=11 1011

-5*(-6) кс=00 0101

микропрограмма:

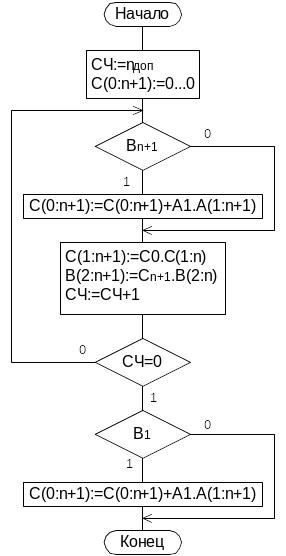
Деление двоичных чисел с фиксированной точкой.

D=A/B,

|A| < 1, |B| < 1

1. |A| >=|B|, |D|>=1, F_пп:=0

2.B=0, F_пп:=1

F_пп – флаг переполнения.

Деление чисел, представленных в прямых кодах.

Числа делятся по модулю, знак числа – сложение по модулю2.

|D|=|A|/|B|

Зн.D=Зн.АЗн.В

Две постановки задачи деления:

1. деление с вычитанием остатка.

Результат деления D и R остаток от деления вычисляются с точностью до n знаков, где n – число информационных разрядов в делимом и делителе.

2. деление с округлением.

Вычисляется только частное D (n-знаковое). Вычисляется n+1 цифра частного для округления, чтобы не накапливалась ошибка.

D_i=0.d₁d₂…d_i, i-цифр

Найти I=1 цифру:

0D-D_i2^-I

D=0 110001

D_i=01101

D-D_i0.0000|₁2ⁱ⁺¹

02ⁱB(D-D_i)B

0 2ⁱ(A-BD_i)B

R_i

R_i – остаток от деления при вычислении i-той цифры частного.

R_i=2ⁱ(A-BD_i)

0R_iB

Пусть d_i+1=0, тогда D_i=D_i+1

R_i+1=2ⁱ⁺¹(A-BD_i+1)= 2ⁱ⁺¹(A-BD_i)=2*2ⁱ(A-BD_i)=2R_i

0R_i+1B; 02R_iB

Если 2R_i<B, то d_i+1=0

Пусть d_i+1=1

D_i+1=D_i+2^-(i+1)

R_i+1=2ⁱ⁺¹(A-BD_i+1)= 2ⁱ⁺¹(A-BD_i-B*2^-(i+1))=2*2ⁱ(A-BD_i)-B=2R_i-B

02R_i-BB

Если 2R_iB, то d_i+1=1

R₀=A

Алгоритм деления с восстановлением остатка.

1. Сч:=0, А0, В0.

2. R:=A-B

3. Если R0, то F_пп:=1, конец.

Иначе R:=R+B.

4 . R:=2R

5. R:=R-B

6. Если R0, то D:=L(D).1

Иначе D:=L(d).0: R:=R+B

7. Сч:=Сч+1

8. Если Сч<n+1, то перейти к п.4

9. Зн.D=Зн.АЗн.В

10. Конец.

Пример:

.1011/.1100

_ .1011

1100

_10100,0>0……….0.00001

1100

_1000.0>0………….0.0011

1100

_100.0>0…………..0.00111

1100

₊отриц.число<0………0.01110

1100

_1000

1100

100>0……………..0.11101

R^t;

R^t+1=R^t+B;

R^t+2=2R^t+1=2R^t+2B;

R^t+3+R^t+2-B=2R^t+2B-B=2R^t+B.

Алгоритм деления без восстановления остатка.

1. Восстановление отрицательного остатка

2. Сдвиг или удвоение остатка

3. Сдвиг и вычитание делителя эквивалентны удвоению отрицательного остатка и прибавлению делителя.

Алгоритм позволяет уменьшить количество микроопераций сложения(на каждую цифру частного выполняется одно сложение, а не 1,5).

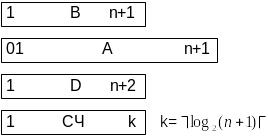
Микропрограмма:

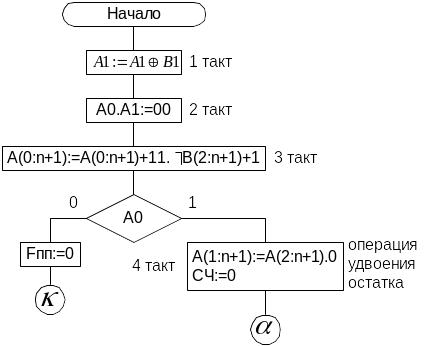
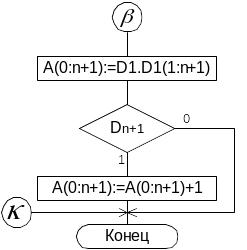
Операции в АЛУ на двоичными числами с плавающей точкой.

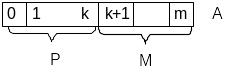
Р – порядок

М – мантисса

А=М*2^Р

Если Р определяет диапазон представления чисел в ЭВМ, то М – точность представления чисел в ЭВМ.

С:=АВ; {+,-,*,/}

Необходимое оборудование:

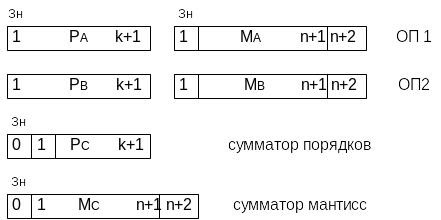
N+2 разряд в мантиссах необходим для округления, т.к. выполнение операций с плавающей точкой связаны с потерей точности.

Операнды (ОП) поступают из памяти в ОА в нормализованном виде; знаковые разряды дублируются только на ОЭ. Результат операции тоже должен быть в нормализованном виде.

Нормализованное число: 1/2|М|1.

Нормализованное число – это число, у которого первая информационная цифра мантиссы равна 1 для положительных чисел и равна 0 – для отрицательных чисел, и знаковые разряды мантиссы при этом одинаковые.

00,11001 – нормализованное число

11,0011 – нормализованное число

Требования для нормализованных чисел:

М_с(0)М_с(2)=1

М_с(0)М_с(1)=0.

Виды нарушения нормализации:

1. Нарушение нормализации влево(переполнение мантиссы).

01,110

01 – для положительных чисел

10 – для отрицательных чисел

Восстановление нормализации в этом случае происходит сдвигом мантиссы на один разряд, при этом мантисса уменьшается в два раза, поэтому порядок нужно увеличивать на 1.

2. Нарушение нормализации вправо(знаковые разряды мантиссы равны, но не выполняется условие: М_с(0)М_с(2)=1).

00.00010

11.110

Восстановление нормализации возможно сдвигом мантиссы влево и уменьшением порядка на 1.

-1/2₁₀=11,100₂ – нормализованное число, не выполняется условие М_с(0)М_с(2)=1;

+1/2₁₀=00,100₂

Исключительные ситуации при нормализации и после выполнения операций с плавающей точкой.

1. Аварийное завершение операции(прерывание).

Мантисса=0, а порядок любой. Ситуация такая называется потеря значимости.

F_пз:=1; Р:=0.

2. При нарушении нормализации влево, после сдвига мантиссы вправо может возникнуть переполнение порядка. Такая ситуация называется переполнение порядка.

F_пп :=1.

3. При нарушении нормализации вправо, после сдвига мантиссы влево может возникнуть отрицательное переполнение порядка. Такая ситуация называется исчезновением порядка.

F_ип :=1.

Микропрограмма нормализации чисел:

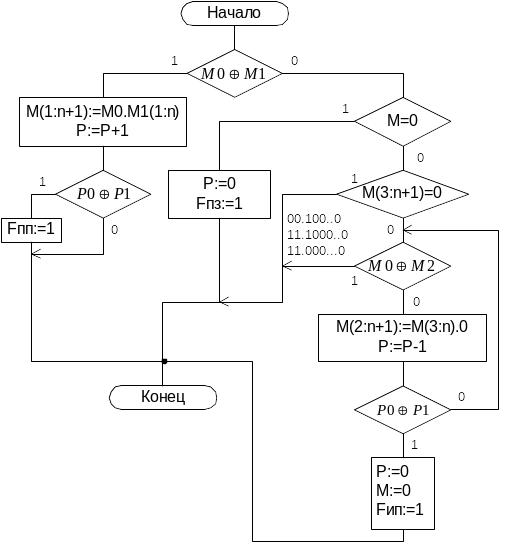
Алгоритм сложения чисел с плавающей точкой.

Даны:

А=М_А*2^Ра

В=М_В*2^Рв

Найти:

С=М_С*2^Рс

Операнды и результат должны быть в нормализованном виде.

1. Проверка особых ситуаций:

Если М_В=0, то С:=А

Если М_А=0, то С:=В

Переход к концу.

2. Выравнивание порядков.

0,5*10³+0,4*10²=0,5*10³+0,04*10³=0,54*10³.

0. Вычисление разности порядков: Р_С:=Р_А-Р_В.

1. Если |Р_С|n+1, то сумма принимается равной числу с большим порядком:

Если Р_С=0, то С:=А;

Если Р_С=1, то С:=В.

Переход к концу.

0. Если Р_С0, то производится уравнивание порядков слагаемых, путем приведения числа с меньшим порядком к числу с большим порядком. Уравнивание порядков выполняется арифметическим сдвигом мантиссы числа с меньшим порядком вправо на число разрядов равное |Р_С|.

Если ЗнР_с=1, то преобразуется М_А.

Если ЗнР_с=0, то преобразуется М_В.

Сдвиг осуществляется следующим образом:

При каждом элементарном сдвиге на 1 разряд из Р_С вычитается 1, если сдвигается М_В, и прибавляется 1, если сдвигается М_А.

Выход из цикла по Р_С=0.

Если М_А и М_В представлены в прямом коде, то старшие освобождающиеся при сдвиге информационные разряды заполняются нулями; если в инверсном коде, то знаковыми разрядами.

3. Мантиссы, полученные после уравнивания порядков, складываются как числа с фиксированной точкой.

М_С:=М_А+М_В.

Порядок суммы принимается равным наибольшему из порядков слагаемого.

Р_С:=max(Р_АР_В).

Отличие от алгоритма сложения с фиксированной точкой – не вырабатывается сигнал переполнения, т.к. возможна нормализация со сдвигом вправо.

4. Округление мантиссы результата осуществляется прибавлением 1 к n+2 разряду сумматора мантисс.

5. Нормализация результата (см. алгоритм выше).

Исключительные ситуации при сложении:

• Потеря значимости;

• Переполнение порядка при нормализации со сдвигом вправо;

• Исчезновение порядка при нормализации со сдвигом влево.

Умножение чисел с плавающей точкой.

С=А*В

Даны:

Р_А, М_А, Р_В, М_В.

Найти:

Р_С, М_С.

1. Порядки складываются по правилам сложения чисел с фиксированной точкой. Мантиссы перемножаются по правилам умножения чисел с фиксированной точкой.

2. Младшие разряды произведения, выдвигаемые в такте сдвига из сумматора мантисс, не сохраняются, кроме n+2 разряда.

3. Результат округляется добавлением 1 в n+2 разряд М_С и нормализуется.

Исключительные ситуации:

• Исчезновение порядка при нормализации со сдвигом влево;

• Переполнение порядков, т.к. имеет место сложение порядков в алгоритме.

Деление чисел с плавающей точкой.

С=А/В.

Р_С=Р_А-Р_В;

М_С=М_А/М_В.

Порядки вычитаются, а мантиссы делятся по соответствующим алгоритмам выполнения операций с фиксированной точкой.

Исключительные ситуации:

• Деление на ноль;

• Исчезновение порядка при нормализации со сдвигом влево;

• Переполнение порядков, т.к. имеет место сложение порядков в алгоритме.

Особенности применяемого алгоритма деления с фиксированной точкой.

В классический алгоритм деления вносятся незначительные изменения:

• М_А перед выполнением деления с фиксированной точкой сдвигается влево на один разряд, порядок увеличивается на 1.

• Предусматривается нормализация со сдвигом влево.

Выполнение операций десятичной арифметики в АЛУ.

Не во всех системах команд есть такие операции. Наличие операций десятичной арифметики целесообразно для несложных расчетов коммерческого характера с простыми формулами, где нужны целочисленные вычисления и невыгодно переводить числа в двоичные представления и обратно, для того чтобы над ними выполнить 2-3 операции.

Десятичные числа представляются в АЛУ в двоично-десятичном коде.

Сложение двух десятичных чисел сводится к последовательной выработке сумм вида:

P_iC_i=A_i+B_i+P_i+1 , где

A_i и B_i – четырехразрядные коды десятичных цифр слагаемых;

P_i+1 – десятичный перенос(перенос со сдвигом 10) из предыдущего младшего десятичного разряда суммы;

P_i – десятичный перенос в следующий старший разряд суммы;

C_i – 4-х разрядный двоичный код цифр суммы

A_i+B_i+P_i+1<=19;

Построение такой схемы достаточно сложное и схема будет сложной, поэтому обычно для сложения десятичных чисел используется обычный двоичный сумматор, который настраивается на уровне микропрограммы применительно к специфике сложения десятичных чисел.

Вычисление десятичной суммы может быть параллельно-последовательным процессом, т.к. двоичный сумматор имеет ограниченную длину, а число десятичных цифр может варьироваться.

Три случая возникающие при сложении десятичных чисел на двоичном сумматоре:

1. 0C_i9 C_i

0010+0011=0101

P_i=0

2. 10C_i15 C_i

1001+0011=1100

P_i=0

надо: P_i=1, C_i=0010

1100

+

0110

P -1.0010 - C_i

3. 16C_i19 C_i 0001

1000+1001=0001 +

P_i=1 0110

0111

Если C_i10, то всегда нужна коррекция.

Алгоритм сложения десятичных чисел.

A>0; B>0; C=A+B.

1. Вычисляется сумма С=а₁а₂..a_n+bb..b (рассматриваются только информационные разряды).

2. С:=С+В

Если перенос старшей тетрады равен1, то фиксируется F_пп:=1.

Иначе переход к концу.

3. Формируется корректирующее слагаемое.

Корректирующая цифра k_i=0000, если P_i=1.

K_i=1010, если P_i=0.

4. Вычисляется сумма: С:=С+Л(суммирование производится с разорванными цепями межтетрадных переносов).

Пример:

134+591=725

0001 0011 0100

+

0110 0110 0110 +6

0111 1001 1010

+

0101 1001 0001 +В

1101 10010 1011 (*)

-

1010 0000 1010 +К

0111 0010 0101

Для того, чтобы преодолеть недостаток, заключающийся в управлении цепями переноса, предложен следующий подход – корректирующие константы уменьшить на 1, перенос в младший разряд сделать равным 1, заведя на него перенос со старшего разряда, либо замкнуть на вход управляющий сигнал.

В этом случае во все тетрады будет идти перенос, но учитываться он не будет.

Пример:

(*) 1101 0010 1011

1001 1111 1001

1

0111 0010 0101

Вычитание десятичных чисел.

С=А-В (A>0, B>0)

B^*=10ⁿ-B

0001 0000 0000 0000

b₁ b₂ b₃

b₁^* b₂^* b₃^*

b_i^*=10-b_i для i=n;

b_i^*=9-b_i для i=1, .. , n-1;

_

C_i=A_i+6+b_i^*=A_i+6+9-b_i=A_i+15-b_i=A_i+b_i

Алгоритм вычитания:

_ _ _

1. С:=а₁а₂..а₃+b₁b₂..b_n+1

2. K=K₁…K_n

K_i=1111, если P_i=1

K_i=1001, если P_i=0.

3. C:=C+K

Перенос со старшей тетрады замкнут на младший разряд двоичного сумматора.

Пример:

725-135=590 А>B

01111 0010 0101

+

1110 1100 1010

1

10101 1111 10000

1111 1001 1111

1

0101 1001 0000

Если А<B, то результат получится в дополнительном коде.

А>B С:=А-B

А<B C:=10ⁿ-|B-A|

Пример:

135-725

0001 0011 0101

+

1000 1101 1010

1

11010 10001 10000

1001 1111 1111

0100 0001 0000

410=1000-590

Для того, чтобы избежать дополнительного сложения используется обобщенный алгоритм, который позволяет получить результат в прямом коде:

Обобщенный алгоритм:

С:=А+В

1. Зн С:=Зн А

2. Если Зн А=Зн В, то выполняется микропрограмма сложения.

Если перенос из старшего информационного разряда P₁=1, то вводится F_пп:=1, иначе переход к концу.

3. Если Зн АЗн В, то выполняется микропрограмма вычитания А-В.

Если перенос из старшего разряда Р₁=0, то знак суммы меняется на противоположный и выполняется микропрограмма В-А.

Пример:

135-725=-590

Зн С:=Зн А

0001 0011 0101

1000 1101 1010

1

11010 10001 10000

С:=В-А

0111 0010 0101

1110 1100 1010

1

и т.д.

Реализация микропрограммы в АЛУ.

Некоторые участки кода используются в различных ветвях алгоритма, существует алгоритм оптимизации ГСА.