Арифметико-логическое устройство эвм как операционное устройство.

АЛУ – это операционное устройство предназначенное для выполнения следующих классов операций:

1. Операции двоичной арифметики над числами с фиксированной точкой.

2. Операции двоичной арифметики над числами с плавающей точкой.

3. Операции десятичной арифметики над целыми десятичными числами, представленные в двоично-десятичном коде.

4. Операции индексной арифметики над целыми двоичными числами без знака.

5. Операции специальной арифметики (сдвиг, нормализация, перевод чисел из одной системы счисления в другую).

6. Логические поразрядные операции (сравнение кодов, инвертирование кодов, конъюнкция, дизъюнкция, сложение по модулю 2).

Типы данных обрабатываемые а АЛУ.

1. Двоичные числа с фиксированной точкой.

0 – положительное число;

1 – отрицательное число.

Если точка зафиксирована слева, то А<1, иначе - А>=1.

Пример:

0,0110 = +6\16

0 0110, = +6

пусть точка зафиксирована слева: А<1.

2. Двоичные числа с плавающей точкой.

А=М*2^Р,

где Р – порядок.

Количество разрядов мантиссы определяет точность представления чисел в ЭВМ.

Количество разрядов порядка определяет диапазон представления чисел в ЭВМ.

3. Целые десятичные числа.

0000 0011 0101 1001

знак 3 5 9

4. Символьные данные.

5. Двоичные коды.

6. у кодов знаковый разряд не выделяется, все разряды равнозначны. Операнды трактуются как коды при выполнении логических поразрядных операций.

Классификация АЛУ.

1. По способу организации:

• Многофункциональные АЛУ, выполняющие весь набор операций в одном устройстве;

• Блочные АЛУ, в них выделяются специализированные блоки для выполнения операции каждого класса.

2. По способу представления и обработки чисел в АЛУ:

   • Параллельные АЛУ, операции производятся над всеми разрядами числа одновременно.

   • Последовательные АЛУ, операции производятся над каждым разрядом отдельно и последовательно.

   • Параллельно-последовательные АЛУ.

3. По взаимодействию АЛУ с центральным устройством управления (процессором):

• Встроенный процессор в АЛУ характеризуется тем, что АЛУ интегрировано в процессор, имеет с ним общие цепи передачи данных и составляет единое устройство.

• Автономные АЛУ.

ЦУУ только загружает АЛУ операндами (регистры Р1 иР2) и инициирует нужную операцию y_i^АЛУ . операция выполняется внутри АЛУ под управлением собственного управляющего устройства АЛУ. Когда выполнение операции заканчино, АЛУ выдает осведомительный сигнал z_АЛУ.

z_АЛУ=1 – АЛУ занято,

z_АЛУ=0 – АЛУ свободно.

Алгоритмы и аппаратное обеспечение операции в АЛУ.

1. операции над числами с фиксированной точкой.

   1. а лгебраическое сложение:

недостаток – задержка переноса.

Знаковый разряд учавствует в операции сложения аналогично всем остальным разрядам.

Пример:

0 0101

+

0 0110

0 1011

вычитание:

если нужно выполнить вычитание, то его заменяют сложением с инверсным кодом числа В^*.

С:=А-В , А>0, В>0.

C:=А+(-В)=А+В^*.

Инверсный код может быть обратным и дополнительным. Любой инверсный код положительного числа совпадает с его прямым кодом.

А=0 0101

А_обр=А_доп=0 0101

Обратный код отрицательного числа получается из его прямого кода инвертированием всех разрядов за исключением знакового.

(10101)_обр=11010 -5

Дополнительный код отрицательного числа получается прибавлением 1 к его обратному коду.

(10101)_обр=11011 В_доп=1-В

Дополнительный код отрицательного числа можно получить из прямого следующим образом:

• проинвертировать все разряды, кроме знакового, к младшему разряду добавить 1(можно прибавлять при суммировании чисел как единичный перенос в младший разряд сумматора):

1 101000

1 01011

+

1

1 011000

• знаковый разряд оставить без изменения, все информационные разряды, начиная с младшего до первого включительно, оставить без изменения, остальные разряды проинвертировать.

1 101000

1010000

правило:

если оба складываемых числа представить в обратных(доп.) кодах, то и сумма получится в обратном (доп.) коде.

Пример:

+6 +5

0. 0110 - 0 0101

(0 0110)_обр=0 0110

(1 10101)_обр=1 1010

0 0110

+

1 1010

0 0000 +

1

0 0001

при сложении в обратных кодах перенос из старшего знакового разряда замыкается на младший разряд. При сложении в дополнительных кодах этот перенос теряется.

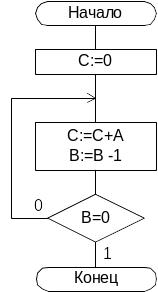
Алгоритм сложения.

1. перевести все слагаемые в инверсный код.

2. выполнить микрооперацию сложения на двоичном сумматоре.

3. перевести результат в прямой код.

Для того, чтобы из приведенной ГСА сложения, получить ГСА вычитания, кроме изменения обозначений (0и1) выходов условной вершины нужно еще проинвертировать знаковые разряды в микрооперациях у₂ и у_3.

Обобщенный алгоритм сложения и вычитания.

C:=C_SB

S-триггер

S=1 – вычитание

S=0 – сложение

микропрограмма обобщенного алгоритма сложения и вычитания

Переполнение разрядной сетки.

Переполнение разрядной сетки может возникнуть только при сложении чисел с одинаковыми знаками.

Пример:

0. 1000

0 1001

1 0001

8/16+9/16=17/16>1

Способы распознавания ситуации переполнения:

1. Переполнение возникает, когда знак суммы отличается от равных знаков слагаемых.

2. Использование модифицированных кодов слагаемых. Модифицированный код числа – это код с удвоенным знаковым разрядом. В памяти числа хранятся с одним знаковым разрядом (в обычных кодах), удвоение происходит при выполнении сложения на входах сумматора.

Пример:

00 1000

+

0 0 1001

01 0001

11 1000

+

11 0111

1 0 1111

Если в результате выполнения операции сложения знаковые разряды отличаются друг от друга, значит произошло переполнение.

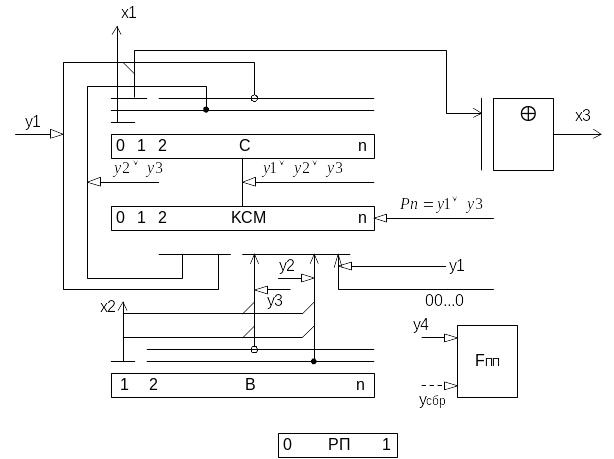
М икропрограмма сложения двоичных чисел с фиксированной точкой.

Структурная схема ОА.

Формирование признака результата.

C=0 ПР РЕЗ = 00

C<0 ПР РЕЗ = 01

C>0 ПР РЕЗ = 10

ПП ПР РЕЗ = 11

Умножение двоичных чисел с фиксированной точкой в АЛУ.

С=А*В

Числа вступают в операцию в прямом коде.

1. умножение с удвоенной точностью.

Разрядность результата в 2 раза больше разрядности операндов.

2. умножение с округлением.

Разрядность результата такая же как разрядность операндов.

С=А*В

Зн С=Зн АЗн В

Замена умножения сложением.

.358*.256

.1011000110

*

.1000000000

1 0110011000000000

1 слож-е 8 сдвигов

умножение “в столбик”

Каждое частное произведение может быть равно 0 или А.

С_i=0, если b_i=0,

С_i=A, если b_i=1.

У множение сводится к вычислению суммы частичных произведений, т.е. к последовательности сложений и сдвигов.

Методы умножения.

С:=А*В

1.1101 А

*

1011. В

Вычисление модуля результата:

1101

*

1011

1101

1101

0000

1101

10001111

вычисление знака:

Зн С=Зн А  Зн В=1 + 0=1

1. Умножение, начиная с младших разрядов множителя со сдвигом суммы частных произведений.

Микропрограмма умножения:

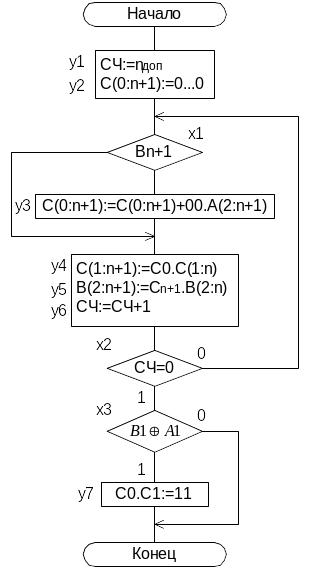
Пример:

нач.сост подгот. слож-е сдвиг слож-е сдвиг сдвиг слож-е сдвиг знак

В 0 1011 0 1011 0 1011 0 0101 0 1101 0 1110 0 1111 0 1111 0 1111 0 1111

С х хххх 00 0000 00 1101 00 0110 01 0011 00 1001 00 0100 01 0001 00 1000 01 1000

А 1 1101 1 1101 1 1101 1 1101 1 1101 1 1101 1 1101 1 1101 1 1101 1 1101

С ч хх 00 00 01 01 10 11 11 00 00

Результат: 11 1000 1111

8/16+15/256=143/256

11/16*13/16=143/256

Правило арифметического сдвига вправо:

Сдвигается та часть сумматора, начиная с разряда переполнения. Знаковый разряд остается на месте, освобождающийся разряд доопределяется знаковым.

Округление результатов.

1 1 1000 1111

+

1

11 1001

Чтобы округлить число, нужно прибавить единицу к старшему отбрасываемому разряду.

окончание микропрограммы

в случае применения округ-

ления