Теория информации 2. Введение в теорию сигналов

2. Введение в теорию сигналов

2.1. Общие сведения и понятия

Понятие сигнала. В технических отраслях знаний термин «сигнал» (от латинского signum – знак) очень часто используется в широком смысловом диапазоне, без соблюдения строгой терминологии. Под ним понимают и техническое средство для передачи, обработки и использования информации, а по существу, материальный носитель определенного информационного сообщения; и физический процесс, представляющий собой материальное воплощение информационного сообщения - изменение какого-либо параметра носителя информации во времени, в пространстве или в зависимости от изменения значений каких-либо других аргументов; и форму представления данных в виде последовательности значений определенной скалярной величины, как правило – амплитуды, измеренной во времени; и смысловое содержание определенного физического состояния или процесса, как, например, сигналы светофора, звуковые предупреждающие сигналы и т.п.

Принимая во внимание изложенное, под термином «сигнал» в строгом смысле этого слова в данном курсе будем понимать определенным образом организованное отображение определенной информации π о характере изменения в пространстве, во времени или по любой другой переменной физических величин (Рис.2.1.1), физических свойств или физического состояния объекта исследований. При этом материальная форма носителей сигналов, равно как и форма их отображения, значения не имеет.

Сигнал - это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а цель обработки сигналов - извлечение сведений, которые отображены в этих сигналах и преобразование этой информации в форму, удобную для восприятия и использования.

Шумы и помехи. При регистрации сигналов, несущих целевую информацию, в сумме с основным сигналом одновременно регистрируются и мешающие сигналы - шумы и помехи самой различной природы (Рис.2.1.2).

Шум – это беспорядочные или случайные колебания различной физической природы, отличающиеся сложностью временной и спектральной структуры. Обычно шумы являются естественным фоном полезного сигнала или дестабилизирующими процессами в аппаратуре измерения и обработки сигналов.

К помехам относят нежелательные физические явления или воздействия внешнего или внутреннего источника, которые нарушают нормальную работу технических средств, или вызывают ухудшение технических характеристик и параметров этих средств.

Выделение полезных составляющих из суммы зарегистрированных сигналов или максимальное подавление шумов и помех в сигнале при сохранении его полезных составляющих является одной из основных задач первичной обработки сигналов.

Рис.2.1.1. Сигнал. Рис.2.1.2. Сигнал с помехами.

Следует заметить, что деление сигналов на полезные и мешающие является достаточно условным. Источниками мешающих сигналов также являются определенные физические процессы, явления или объекты. При выяснении природы мешающих сигналов они могут переводиться в разряд информационных.

Размерность сигналов. Простейшими сигналами являются одномерные сигналы, как, например, звуковые сигналы, сейсмические импульсы s(t) и т. п. Значения одномерных сигналов зависят только от одной независимой переменной, как, например, на Рис. 2.1.1 и 2.1.2.

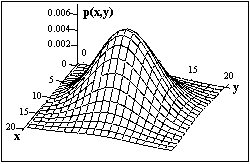
Рис. 2.1.3. Двумерный сигнал.

В общем случае сигналы являются многомерными функциями пространственных, временных и прочих координат – интенсивность компьютерного изображения р(x,y) (Рис. 2.1.3), сейсмическая волна вдоль профиля s(x,t) и т. п.

Многомерные сигналы могут иметь различное представление по своим координатам. Так, полный акустический сигнал сейсмического профиля дискретен по пространству (точкам расположения приемников) и непрерывен по времени.

В общем случае многомерный сигнал может рассматриваться, как упорядоченная совокупность одномерных сигналов. С учетом этого при анализе и обработке сигналов многие принципы и практические методы обработки одномерных сигналов, математический аппарат которых развит достаточно глубоко, распространяются и на многомерные сигналы. Физическая природа сигналов для математического аппарата их обработки значения не имеет. Вместе с тем обработка многомерных сигналов имеет свои особенности и может существенно отличаться от одномерных сигналов в силу большего числа степеней свободы. Так, при дискретизации многомерных сигналов имеет значение не только частотный спектр сигналов, но и форма растра дискретизации. Что касается порядка размерности многомерных сигналов, то ее увеличение выше двух не изменяет принципов и методов анализа данных и сказывается только на техническом усложнении вычислений. Учитывая эти факторы, при дальнейшем рассмотрении ограничимся, в основном, одно- и двумерными сигнальными функциями, а в качестве универсальной независимой переменной будем использовать, как правило, переменную t для одномерных сигналов и переменные x, t или x, y для двумерных сигналов, безотносительно к их физическому содержанию.

Математическое описание сигналов. Сигналы могут быть объектами теоретических исследований и практического анализа только в том случае, если указан способ их математического описания - математическая модель сигнала.

Слово «модель» произошло от латинского modelium, что означает: мера, способ, образ, описание. Назначение модели состоит в том, что она сохраняет лишь некоторые наиболее важные для исследователя черты объекта-оригинала.

Математическое описание позволяет абстрагироваться от физической природы сигнала и материальной формы его носителя, проводить классификацию сигналов, выполнять их сравнение, устанавливать степень тождества или различия, моделировать системы обработки сигналов. Как правило, описание сигнала задается функциональной зависимостью значений определенного информационного параметра π сигнала от независимой переменной (аргумента) – s(х), y(t) и т.п. Функции описания сигналов могут быть как вещественными, так и комплексными.

Сделаем одно замечание по терминологии описания сигналов. В работах по обработке сигналов значения величины сигнала (отсчеты значений по аргументу) часто именуют координатами сигнала. Под понятием координат сигнала будем понимать не только какие-либо пространственные координаты, но и любые другие аргументы, на числовой оси которых отложены значения или отсчеты сигнала (пример на Рис. 2.1.1).