2. Порядок выполнения работы

1. Изучить методические указания и ответить на контрольные вопросы.

2. Получить у преподавателя номер варианта.

3. В соответствии с пунктом 1:

• осуществить приближенную оценку корней заданной системы нелинейных уравнений;

• произвести уточнение корней, с этой целью представить математическую формулировку решения системы нелинейных уравнений по двум методам, составить схему алгоритма решения и написать программу в среде СИ++ или MathCad.

4. Отладить программу и получить результаты расчетов.

5. Провести анализ полученных результатов.

3. Краткие теоретические сведения

Решение систем нелинейных уравнений состоит из 2-х этапов:

- отделение корней;

- уточнение корней в отдельных интервалах.

Задача отделения корней даже для нелинейных уравнений может вызвать значительные трудности. А в случае систем нелинейных уравнений эта задача еще более усложняется.

.

Отделение корней будет заключаться в приближенном определении точек пересечения 2-х кривых f(х,у), (х,у). Для этого уравнения f(x,y)=0 и (x,y)=0 представить в виде y=f*(x) и y=*(x) и построить графики. Точка пересечения определит корни уравнения.

Например, имеется система нелинейных уравнений:

.

Преобразуем её в

и построим графики (рис. 1).

Из рис. 1 видно, что корень уравнения единственный и находится в области 6  x  10, –6  y  –2.

Рассмотрим два метода уточнения корней, которые используются для решения систем нелинейных уравнений.

Рассмотрим систему нелинейных уравнений 2-го порядка в общем виде:

. (1)

Однако необходимо учитывать, что метод Ньютона может использоваться и для систем уравнений более высокого порядка.

Рис. 1. Отделение корней

Метод Ньютона

Выберем х₀ и у₀ в качестве грубого приближения к решению, х₀ и у₀ могут выбираться либо на этапе отделения корней, либо из физических соображений или при постановке задачи.

Для реализации последовательного приближения грубого приближения к решению (точному) х и у необходимо записать в алгоритм поиска наиболее точного решения в следующем виде:

.

Т.е. для решения системы уравнений необходимо указать правила нахождения добавок h_i, k_i.

Для этого введем следующее обозначение

. (2)

Подставим (2) в систему (1):

. (3)

Разложим уравнения системы (3) в ряд Тейлора в окрестностях точки (х₀, у₀), при этом ограничимся линейными членами разложения

, (4)

Если пренебречь ₁ и ₂, то получим систему линейных уравнений относительно h и k, т.к.

k = - y₀ + y; h = x₀ - x

. (5)

Решение системы (5) даст неизвестные h и k, которые приближают х₀, y₀ точному решению, но точного значения корня не обеспечивают (вследствие пренебрежения остаточными членами разложения ₁ и ₂).

Т.к. f(x₀, y₀), ( x₀, y₀), f’_x( x₀, y₀), f’_y( x₀, y₀), _x^’( x₀, y₀), _y^’( x₀, y₀) – const, систему уравнений (5) можно представить в привычном (нормальном виде):

.

Решение системы может быть получено с использованием методов решения систем линейных уравнений, например, правилом Крамера:

; , где

Определитель матрицы, составленный из первых производных системы уравнений, называется Якобианом. После того как h и k найдено, необходимо повторить процесс поиска новых значений h и k и т.д., до тех пор пока решение не достигнет заданной степени точности . При этом в качестве начального приближения выбирается всякий раз очередное приближение к решению, т.е. итерационный процесс поиска можно представить в следующем виде:

. (6)

Условием прекращения поиска решения является выполнение, следующего условия:

. (7)

Причем эти условия должны выполняться одновременно.

Таким образом, поиск решения выполняется при реализации следующей последовательности действий:

1) выбираются начальные значения х₀ и у₀;

2) для этих значений рассчитываются значения функций f, , f'_x, f'_y, ’_x, ’_y;

3)решается система линейных уравнений (5), т.е. находятся значения h и k;

4)по формулам уравнений (6) находятся значения х, у. Процесс поиска, т.е. действия (2)-(4) выполняются до тех пор, пока не выполнится условие достижения заданной степени точности (7).

Рис. 1. Блок-схема решения системы нелинейных уравнений методом Ньютона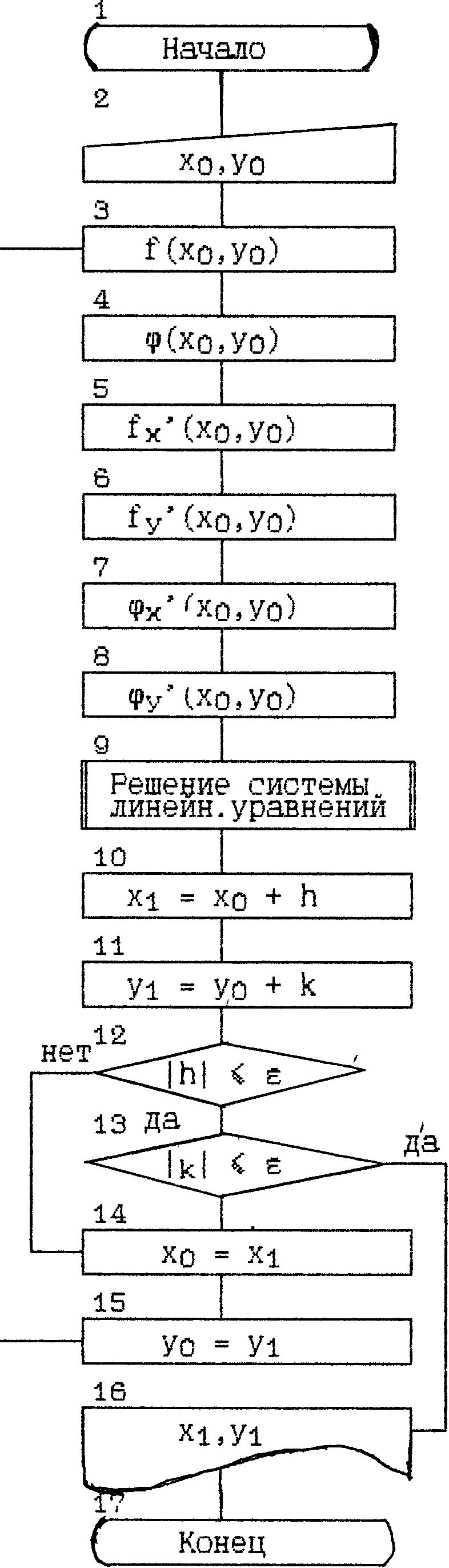

Метод итераций

Запишем систему нелинейных уравнений

. (8)

Приведем ее к нормальному виду

. (9)

Выберем грубые начальные приближения к решению х₀, у₀ подставляя их в правую часть системы можно подучить некоторые новые приближения x₁,у₁. Повторяя вновь процесс подстановки найденных значений в первую часть системы (9) получим последовательность приближений.

Последовательность х_i, у_i будет сходиться к решению системы (8) при выполнении следующий условий сходимости.

Условия сходимости последовательности х_i у_i.

1. Если в замкнутой окрестности R имеется только один корень (действительный)

Для двумерного случая замкнутая окрестность R определяется следующим соотношением:

y

a₂

b₂

а₁ b₁ x

Под корнем будем понимать вектор решений, который в двумерном случае имеет 2 компонента х и у.

2. Функции f₁ и ₁ в области R должна быть непрерывна и дифференцируема.

3. Выполняются следующие условия в R.

или

При выполнении всех трех условий последовательность х_i y_i имеет предел, т.е. сходится и этот предел является решением системы уравнений.

Начальные приближения должны выбираться в области R. Условием достижения заданной степени точности является выполнение следующих условий:

.