1

Лекция № 10 Математика эпохи Возрождения

XV и XVI ст. вошли в историю под названием эпохи Возрождения, т.е. возрождения уровня науки, искусства, который был, достигнут в период античности.

Математика развивалась главным образом в растущих торговых городах, под непосредственньм влиянием торговли, навигации, астрономии и землемерия. Центрами новой жизни стали итальянские города, т.е. города Центральной Европы: Нюрнберг, Вена, Прага. После падения Константинополя в 1453 г., когда Византийская империя перестала существовать, многие ученые греки переселились в города Запада, возрос интерес к оригинальным греческим произведениям. Одной из ведущих математических фигур XV ст. является Иоганн Мюллер из Кенигсберга или Региомонтанус - замечательный вычислитель, печатник и ученый. Он усердно переводил, публиковал доступные ему математические рукописи классиков среди них Птолемей, Аполонии, Герон, Архимед. Его главное собственное произведение - "О различных треугольниках" (1464 г.) - введение в тригонометрию. Здесь содержится теорема синусов для сферического треугольника. Все теоремы все еще формулируются словесно. Тригонометрия становится самостоятельной наукой, не зависящей от астрономии. Подобное было сделано Насир-ад-Дином в XIII ст., но его труды не получили дальнейшего развития.

Много труда положил Региомонтанус и на вычисление тригонометрических таблиц, он составил таблицу синусов с интервалом в одну минуту.

Заметным явлением в истории математики была деятельность францисканского монаха Луки Пачоли (около 1445-около 1515). Его книга "Сумма знаний по арифметике, геометрии, отношением и пропорциональности" - это одна из первых печатных математических книг (1494 г.). Она содержала правила арифметических действий, алгебраические и тригонометрические вычисления. Отныне использование индийско-арабских цифр стало общепринятым, а арифметические обозначения в этой книге не слишком отличаются от наших. Пачоли закончил свою книгу замечанием, что решение

уравнений х³ + тх = п, х³ + п = тх столь же невозможно при современном ему состоянии науки, как и квадратура круга.

Это стало отправной точкой для математиков Болонского университета. Древние греки и восточные народы пытались решать уравнения третьей степени, но они только численно решили несколько частных случаев. Болонские математики стремились найти общее решение уравнений третьей степени.

Эти уравнения можно было свести к трем типам:

х³ + px = q, x³ = px + q, x³ + q = px, где p, q > 0. Они были исследованы

профессором Сципионом Ферро (умер 1526 г.), однако он никогда не публиковал своих решений и рассказывал о них лишь близким друзьям. После смерти Ферро венецианский мастер счета, по прозвищу Тарталья (заика), переоткрыл его приемы (1535 г.)- Он публично продемонстрировал свои результаты, но держал в тайне метод их получения. Он раскрыл свои соображения лишь ученому доктору из Милана, Иерониму Кар дано. который поклялся, что будет хранить их в тайне. Однако в 1545 г. Кардано опубликовал книгу "Великое искусство или об алгебраических правилах", в которой описал метод Тартальи (с признанием заслуг автора), а также открытый Луиджи Феррари (1522-1565), учеником Кардано, метод решения в радикалах уравнений четвертой степени.

Полученное решение известно теперь как формула Кардано, и в случае уравнения

х + px + q = О имеет вид:

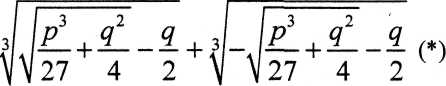
О но содержит выражение вида \Ja + y}b , отличные от евклидовых.

Кардано рассматривал и отрицательные числа, называя их "вымышленными", но он не был в состоянии что-либо сделать в так называемом "неприводимом" случае уравнения третьей степени, когда все коэффициенты и корни кубического уравнения

х + px + q = 0 были действительньми, а по формуле Тартальи-Кардано (*) приходится

под кубическим корнем извлекать корень квадратный из отрицательного числа. Вот пример такого уравнения:

х — 21х + 20 = 0, \J—10 + v243 + \—\0 — >J—243 , оно имеет действительные корни: -5,1,4.

Эта трудность была преодолена болонским математиком Рафаэлем Бомбелли, чья "Алгебра" появилась в 1572 г. В этой книге ив" Геометрии", написанной около 1550 г. (осталась в рукописи), он вводит последовательную теорию мнимых и комплексных

чисел. Он записывает, 3/ как V0 - 9 . Это позволило Бомбелли разрешить неприводимый случай, показав, например, что:

2 + V0-2209 =4 + л/0^Т Однако полное признание комплексных чисел пришло лишь в XIX ст. На границе эпохи Возрождения и Нового времени проходит деятельность выдающегося математика Франсуа Виета (1540-1603). Ф. Виет-французский юрист,

3

состоявший при дворе Генриха IV, свел решение Кардано кубического уравнения к тригонометрическому, и при этом в "неприводимом" случае, дело обошлось без введения

выражений вида л/0 — а.

Алгебра в его трудах стала общей наукой про алгебраические уравнения, которая основывается на символических обозначениях ((прежнее) использование численных коэффициентов препятствовало общему рассмотрению алгебраических задач, математическую символику после Л. Пачолли развивал^ немецкий! алгебраичее?ж& "коссисты" (от cosa - "вещь", "нечто", обозначали неизвестное) М. Штифель, Адам Ризе, но их работы написаны с помощью очень сложных обозначений). Виет использует буквы для выражения численных коэффициентов, знаки "+" и "-" применяет в современном смысле. Но его алгебра все же еще отлична от нашей из-за того, что Виет придерживается греческого принципа однородности: отрезки складывать только с отрезками, площади с площадями, объемы с объемами. Даже существовали сомнения: имеют ли смысл уравнения выше третьей степени.

Виет открыл теоремы про зависимости между коэффициентами и корнями алгебраических уравнений, доказал ряд формул плоской и сферической тригонометрии.

Нидерландский инженер Симон Стевин (1548-1620) в 1555 г. опубликовал книгу "Десятая", где впервые в Европе изложил теорию десятичных дробей и десятичную систему мер. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов. Некоторые математики XVI ст. занимались сопоставлением арифметической и геометрической прогрессий с целью облегчить работу с тригонометрическими таблицами. Михаэль Штифель (1486-1567) (священник) дал

словесную формулировку формулы (a + Z>) , где ueN, выдвинул идею логарифма,

идею многомерного обобщения куба.

Математика находит широкое применение в раскрытии тайн природы. В 1543 г. вышла работа Коперника "Про вращение небесных сфер". Математические методы широко используют в живописи Леонардо да Винчи и Альбрехт Дюрер, в физических исследованиях - Галилей.

Однако введением понятия логарифма мы обязаны шотландскому лорду Джону Неперу. Автор в 1614 г. напечатал свое "Описание удивительного канона логарифмов". Основная его идея: построение двух последовательностей чисел, связанных, так что когда одна из них возрастает в арифметической прогрессии, другая опадаот в геометрической. При этом произведение двух чисел друлЬй последовательности находится в простой зависимости от суммы соответствующих чисел первой и умножение можно свести к

4

сложению. Идею Непера развил его почитатель лондонский профессор Генри Бриг^с в "Логарифмической арифметике". Построенные ими последовательности соответствовали

в современных обозначениях формуле: у = 10* .

Лекция № 10 Математика эпохи Нового времени

XVII-XVIII ст. были эпохой технической и научной революции, которая началась в XVI ст.

На конец XVI ст. математика состоит из арифметики, алгебры, геометрии и тригонометрии. В XVII ст. появляются новые математические дисциплины: аналитическая геометрия, проективная геометрия, теория вероятностей и выдающееся открытие XVII в. — исчисление бесконечно малых, которое в свою очередь, способствовало возникновению — теории бесконечных рядов, интегрированию обыкновенных дифференциальных уравнений и вариационному исчислению. Одновременно продолжались исследования в алгебре, тригонометрии, создавались различные методы приближенных вычислений.

Математики Нового времени еще в большей мере были одновременно астрономами, физиками, математиками и философами.

Новые задачи требовали создание новой математических методов. Проверяя второй закон движения планет, немецкий математик Иоганн Кеплер (1571-1630) решил нон;ую задачу — вычислил площадь эллиптического сектора, а в своей "Стереометрии винных бочек" (1615 г.) он, вычисляя объемы тел, получающихся при вращении конических сечений вокруг оси, лежащей с ними в одной плоскости.

Галилео Галилей дал нам новую механику свободно падающих тел, был основателем теории упругости и защитником системы Коперника. В своих "Беседах" (1638 г.) Галилей пришел к математическому изучению движения, к зависимости между расстоянием, скоростью и ускорением.

Итальянский математик, профессор Болонского университета Бонавентура Кавальери в своей книге "Геометрия" (1635 г.) построил упрощенную разновидность исчисления бесконечно малых, основанную на схоластическом представлении о неделимых, так, что точка порождает при

движении линию, а линия — плоскость. Таким образом, у Кавальери не было бесконечно малых или атомов.

а-

Он получил свои результаты с помощью "принципа Кавальери": два тела одинаковой высоты имеют одинаковые объемы, если плоские сечения этих тел на одинаковом уровне имеют одинаковые площади. Это позволило ему выполнить вычисление, равносильное интегрированию многочленов.

Возникновение аналитической геометрии

В 1637 г. опубликована "Геометрия" французского математика и философа Рене Декарта. В алгебру включается вся область классической геометрии. Идею переменной величины и использование прямоугольных координат Декарт положил в основу новой математической дисциплины -аналитической геометрии. Заслугой Декарта является также то, что он отбросил ограничение однородности его предшественников. Теперь х², х³, ху рассматривались как отрезки. Алгебраическое уравнение стало

соотношением между числами.

Аналитическая геометрия появилась под влиянием книги Декарта, Но "Геометрия" сама по себе вряд ли может рассматриваться как первый трактат по этому предмету.

Следующий шаг к идее современной аналитической геометрии сделал Пьер Ферма (1601-1665), юрист из Тулузы. Во "Введении" Ферма мы находим уравнения:

,2 2 2 ~> 2 | 2 2 / 2

у - тх, ху — к , х + у —а , х ±а у = о

Для прямых линий и конических сечений относительно системы (обычно перпендикулярных) осей. Работа Ферма написана в обозначениях Виета. Под влиянием Декарта написаны также "Трактат о конических сечениях" (1655 г.) Джона Валлиса, "Основы кривых линий" Иоганна де Виета, но прогресс в этой области шел медленно, даже книга Лопиталя "Аналитический трактат о конических сечениях" (1707 г.) - это немногим более чем перевод Аполлония на язык алгебры. Первым, кто серьезно работал с алгебраическими уравнениями, был Ньютон при исследовании

кривых третьего порядка (1703 г.), а первую аналитическую геометрию конических сечений, находим только во "Введении" Эйлера (1748 г.).