Тема №4 «Динаміка твердого тіла»

1. Момент імпульсу твердого тіла. Момент інерції.

2. Рівняння динаміки обертального руху.

3. Кінетична енергія тіла, що обертається.

4. Закон збереження механічної енергії.

5. Сили тертя. Сухе і в’язке тертя.

6. Пружні властивості твердого тіла. Сили пружності.

7. Основні види деформації. Закон Гука.

8. Методи дослідження механічних властивостей сировини і матеріалів.

Якщо напрям сили, яка діє на закріплене в одній точці тверде тіло, проходить через точку закріплення, то очевидно, що ця сила не змінить положення тіла, оскільки дія сили буде зрівноважена силою, що закріплює тіло. Тому стан рівноваги чи стан руху тіла можна змінити лише силою, прикладеною до тіла по лінії, що не проходить через точку закріплення.

Аналіз руху тіла при довільному положення точки прикладення сили до твердого тіла є достатньо складною задачею. Тому розглянемо спочатку плоский рух тіла, при якому всі точки тіла рухаються по паралельних площинах.

Поняття моменту сили нами вже розглядалося. Він, у даному випадку, і буде мірою дії сили на тверде тіло.

Розглянемо такий дослід. На гладкий стіл покладемо дощечку, в яку в довільній точці заб’ємо цвях. До цвяха прив’яжемо нитку, за яку тягтимемо. Дощечка почне рухатися так, що прискорення центра інерції співпаде з напрямком прикладеної сили. Крім того, дощечка почне обертатися навколо вертикальної осі. Змінюючи положення гвіздка на дощечці, можна помітити, що обертання буде тим повільнішим, чим ближче до центра інерції буде вбитий цвях. У цьому випадку дощечка здійснюватиме поступальний рух без обертання, оскільки момент сили відносно вертикальної осі буде рівним нулю.

Отже, можна зробити висновок, що обертання залежить від момента зовнішньої сили відносно вертикальної осі, яка проходить через центр інерції. Якою є ця залежність?

Враховуючи, що при умовах експерименту прикладена сила буде прагнути повернути тіло навколо осі, що приходить через точку закріплення, моментом сили буде векторний добуток сили на радіус-вектор точки її прикладення:

(4.1)

або

, (4.2)

де h – плече сили. Визначення моменту сили як векторної величини дає можливість вказати напрям осі, навколо якої сила прагне повернути тіло.

При розгляді законів руху твердого тіла важливу роль відіграє момент кількості руху відносно деякої довільної точки, яку зазвичай називають полюсом.

Моментом кількості руху (імпульсу) окремої матеріальної частинки тіла масою Δm_і відносно даної точки називають векторний добуток радіус-вектора частинки R_і на вектор кількості руху цієї частинки . Тоді момент імпульсу всього твердого тіла визначають як суму моментів імпульсу всіх частинок цього тіла:

. (4.3)

Отже, загальний закон плоского руху твердого тіла як обертання його навколо нерухомої осі, що проходить через полюс, можна записати так:

, (4.4)

або похідна від момента імпульсу дорівнює сумі моментів зовнішніх сил:

. (4.5)

Якщо зовнішня сила направлена до осі, яка проходить через центр інерції, то і . Якщо у початковий момент часу, до прикладення сили, тіло перебувало у спокої, тобто  = 0, то й надалі кутова швидкість дорівнюватиме нулю. Тобто, тіло буде здійснювати поступальний рух, якщо лінія рівнодійної зовнішніх сил проходить через вісь, на якій знаходиться центр інерції, і тіло починає рух зі стану спокою.

Якщо ж у початковий момент часу тіло мало деяку кутову швидкість ω₀, тобто тіло оберталося, то воно й далі буде обертатися з тією ж кутовою швидкістю, оскільки кутове прискорення рівне нулю.

Відзначимо частковий випадок руху, що виникає під дією пари сил, рівних за величиною й протилежних за напрямком. Під дією такої пари сил тіло здійснюватиме обертання навколо осі, що проходить через центр інерції й перпендикулярної до площини руху тіла, не залежно від того, де прикладені сили.

Я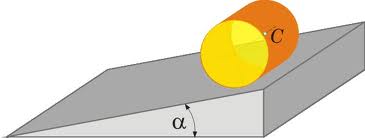 к приклад плоского руху розглянемо скочування циліндра чи колеса по площині. Вісь циліндра рухається з деякою швидкістю v₀, і тіло циліндра здійснює обертання з кутовою швидкістю ω. Якщо циліндр котиться по площині без ковзання, то між цими швидкостями справедливе таке співвідношення:

, (4.6)

де R₀ – радіус циліндра. Якщо рівність (4.6) не виконується, то точка дотику циліндра до площини ковзатиме – циліндр буде котитися з ковзанням.

В будь-якому випадку швидкість точок циліндра можна визначити за формулою

, (4.7)

де – вектор віддалі від осі циліндра доданої точки.

Р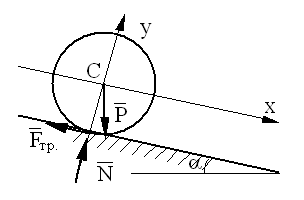 озберемося в динаміці кочення циліндра. Нехай циліндр скочується з похилої площини, що утворює кут α з горизонтом. На циліндр діють три сили: сила тяжіння Р, сила нормального тиску площини на циліндр N і сила тертя циліндра до площини F, що лежить у заданій площині. Оскільки циліндр не покидає площини під час руху, то прискорення центра мас у напрямку перпендикуляра до площини дорівнює нулю; звідси випливає, що

. (4.8)

З іншого боку, складова всіх сил, паралельна до похилої площини, рівна

. (4.9)

Ця сила визначає прискорення центра мас циліндра чи прискорення його поступального руху вздовж похилої площини, тому величина прискорення дорівнює

, (4.10)

де m – маса циліндра. Кутове прискорення, що визначається моментом сили тертя і моментом інерції циліндра відносно його осі, дорівнюватиме

, (4.11)

де R₀ – радіус циліндра.

Використовуючи співвідношення (4.6) між кутовим і лінійним прискоренням, отримаємо:

, (4.12)

. (4.13)

О тже, прискорення поступального руху залежить лише від кута нахилу площини і відношення . Чим більше це відношення, тим менше прискорення.

Нехай на вісь насаджений диск-маховик, який опускається на двох нитках, накручених на вісь. Нитки повністю розмотуються з осі, маховик продовжує обертальний рух в попередньому напрямку, що приводить до закручування ниток на вісь із сповільненням руху диска. Маховик деякий час продовжуватиме рух вгору-вниз, через що такий пристрій називають маятником Максвелла. Складемо рівняння руху такого маховика. Нехай Р – сила тяжіння, f – сила натягу нитки, R – радіус валика, І – момент інерції маховика. Тоді рівняння поступального руху матиме вигляд:

, (4.14)

а рівняння обертального руху –

, (4.15)

Враховуючи зв’язок між лінійною та кутовою швидкостями, можна записати співвідношення між кутовим та лінійним прискореннями:

. (4.16)

Звідси можемо отримати вираз для розрахунку прискорення центра мас маятника

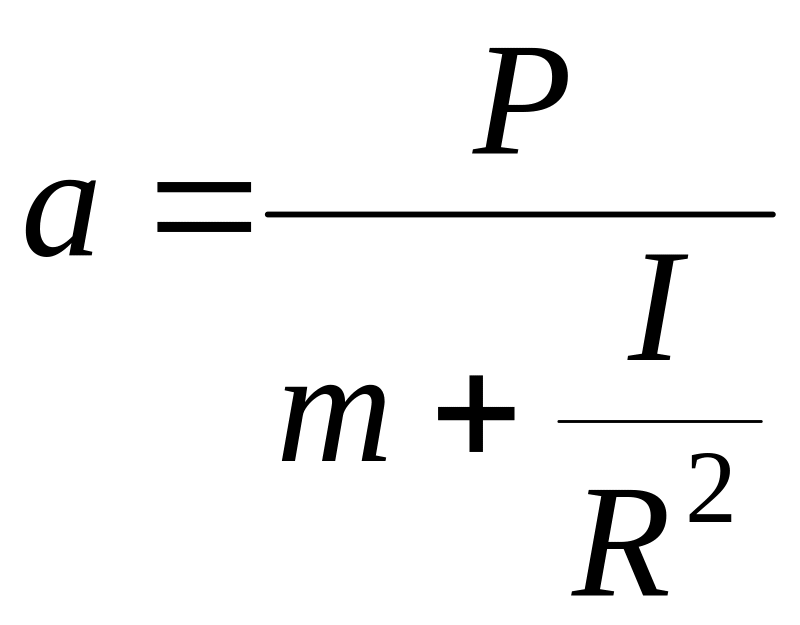(4.17)

та сили натягу нитки

. (4.18)

В одному з попередніх прикладів ми згадали про існування сили тертя. Такі сили існують у всіх механічних системах і явищах, і пов’язані з переходом одного виду енергії в інший. Як правило, механічна енергія внаслідок цих сил переходить у теплову.

Фізичний характер сили тертя може бути різним. Вона може виникати при русі тіла або у стані спокою, коли тіло нерухоме (в такому випадку її так і називають силою тертя спокою).

Робота сил тертя є від’ємною, оскільки сама сила напрямлена проти руху. Отже, енергія переходить в такому випадку від тіла, на яке дія сила тертя. Кінетична енергія зменшується завжди, якщо на тіло діє лише сила тертя:

. (4.19)

При терті спокою немає руху, тому робота не виконується і перетворення енергії відсутнє.

Розрізняють два види тертя: 1) тертя при сухих поверхнях твердих тіл; а також 2) тертя при рідкому чи газоподібному середовищі. Перший вид тертя скорочено називають сухим, а другий – в’язким тертям.

При сухому терті може виникати сила тертя спокою, а при в’язкому – ні. А, отже, сили в’язкого тертя завжди пов’язані з переходом механічної енергії в теплову.

Вивчаючи закони механіки твердих тіл, ми нехтували їх деформацією, вважаючи, що вона є незначною і не впливає на рух цих тіл. Однак, в багатьох задачах механіки потрібно знати закони, які пов’язують дію сил на тіло з тими деформаціями, які викликають ці сили.

П ри деформації не можна переносити силу по лінії її дії, оскільки вона буде різною залежно від того, де вона прикладена. Тільки у пружному тілі в у певному інтервалі зміни величини сил і деформацій дані сили однозначно визначають самі деформації і навпаки.

Розглянемо найпростіший вид деформації – розтягування (чи стискування) однорідного стержня (циліндра) вздовж його осі під дією сили F.

Якщо матеріал стержня однорідний, то всі однакові шматочки стержня будуть однаково розтягнуті однаково при заданому навантаженні. Стержень матиме однорідну деформацію розтягнення, яку можна охарактеризувати відносним видовженням

, (4.20)

де Δl₁ – видовження якогось відрізка стержня, що мав початкову довжину l₁. з умови рівноваги випливає, що сили, прикладені до кінців будь-якого відрізка стержня, рівні за величиною й протилежні за напрямком. Оскільки сказане справедливо для довільного відрізка, отже, в будь-якому поперечному перерізі виникають зусилля, що рівні F.

Якщо матеріал однорідний, то можна вважати, що зусилля розподілене по поверхні поперечного перерізу. Величину такого зусилля, яке дія на одиницю площі поперечного перерізу, називають напруженням і позначають σ. Воно дорівнюватиме:

. (4.21)

Як показує дослід, відносна деформація ε визначається напруженням σ.

Збільшуватимемо навантаження і спостерігати за зміною деформації. При цьому можна отримати діаграму залежності між напруженням і деформацією:

При невеликих зусиллях напруження і деформація будуть пропорційними. Так продовжуватиметься до точки А. Далі деформація буде наростати швидше, крива викривиться у бік видовження, а на відрізку Б-В деформація практично не залежатиме від прикладеного зусилля. Далі область деформацій називається областю текучості або областю пластичних деформацій. Далі, зі збільшенням навантаження, крива вийде не максимум у точці Д, і потім, спадаючи обірветься внаслідок розриву стержня.

Початкова ділянка кривої є прямою лінією; на цій ділянці, приблизно до точки А, залежність між напруженням і деформацією можна представити простим законом прямої пропорційності:

, (4.22)

який носить назву закону Гука. Постійний коефіцієнт пропорційності Е, що має розмірність Н/м², називають модулем Юнга; він є однією з важливих характеристик матеріалів. Область навантажень, в якій закон Гука справедливий, називають областю пропорційності. Межа пропорційності і межа пружності, в загальному, для різним матеріалів можуть і не співпадати.

Отже, деформацію називатимемо пружною, якщо вона зникає після видалення навантаження, яке її викликало, і пластичною, якщо після зняття навантаження вона не зникає (у всякому разі, повністю). Усі реальні тверді тіла при деформації більшою чи меншою мірою мають пластичні властивості. При деяких умовах пластичними властивостями тіл можна знехтувати, як це і робиться в теорії пружності. Тверде тіло з достатньою точністю можна вважати пружним, тобто воно не виявляє помітних пластичних деформацій, поки навантаження не перевищить певної межі (межі пружності).

Вимірювання деформації відбувається або в процесі випробування матеріалів з метою визначення їх механічних властивостей, або при дослідженні споруди безпосередньо чи на моделях для висновку про величину напруг. Пружні деформації дуже малі, і їх вимірювання потребує високої точності. Найпоширеніший метод дослідження деформації – за допомогою тензометрів.

Крім того, широко застосовуються поляризаційно-оптичний метод дослідження напруги, рентгеноструктурний аналіз.