Застосування визначеного інтеграла у фізиці.

Обчислення шляху за відомим законом зміни швидкості.

Раніше було встановлено, що є первісною для функції , яка виражає закон зміни швидкості. Оскільки шлях, який пройде тіло за інтервал часу від до , є приростом функції (приріст первісної), який виражається через інтеграл за формулою Ньютона – Лейбніца, то 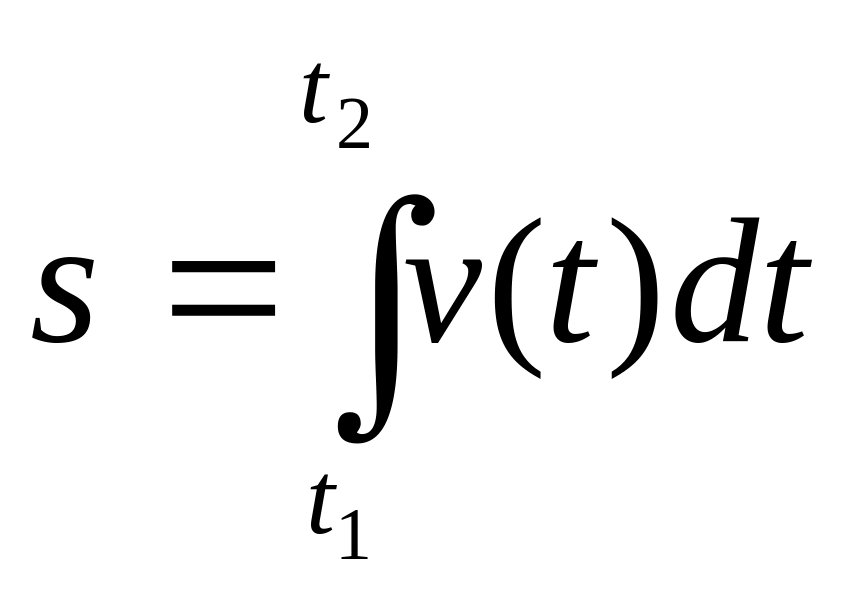за умови , що функція неперервна.

Приклад 14. Тіло рухається прямолінійно зі швидкістю, яка змінюється за законом (м/с). Знайти шлях, який пройшло тіло за інтервал часу від с до с.

Розв’язання.

(м).

Відповідь: 10 м.

Обчислення роботи змінної сили.

Нехай тіло, що розгля­дається як матеріальна точка, рухається під дією змінної сили F(х), напрямленої вздовж осі Ох. Знайдемо формулу для обчислення роботи при переміщенні тіла з точки х = а у точку х = b.

Нехай А(х) — робота при переміщенні тіла з точки а у точ­ку х. Надамо х приросту х. Тоді А(х + х) - А(х) — робота, яка виконується силою F(х) при переміщенні тіла з точки х у точку х + х. Коли х 0, силу F(х) на відрізку [х; х + х] вважатимемо сталою, що дорівнює F(х). Тому А(х + х) - . Звідси .

Тоді , або, за означення похідної, А`(x) =F(x).

Остання рівність означає, що А (х) є первісною для функції F(х). Тоді, за формулою Ньютона — Лейбніца, ,

оскільки А(а) = 0.

Отже, робота змінної сили F(х) при переміщенні тіла з точки а на точку b дорівнює .

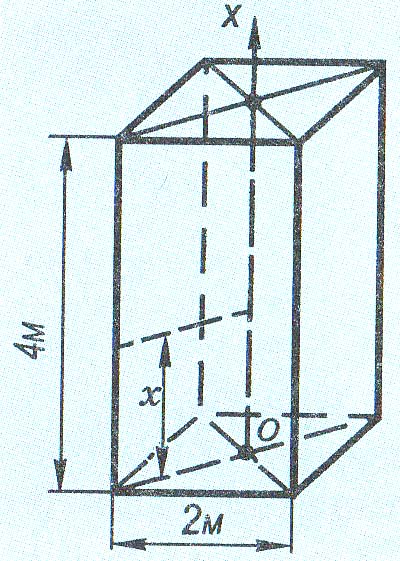
Приклад 15. Обчислити роботу, яку треба виконати, щоб викачати воду з ями глибиною 4 м, що має квадратний пе­реріз зі стороною 2 м. Густина води р = 10³ кг/м³.

Розв'язання. Спрямуємо вісь Ох вздовж діючої сили (мал. 58). Значення сили F(х), що діє на переріз прямокутного паралелепіпеда площею 4 м², визначається вагою шару води, що знаходиться вище від цього перерізу. Отже,

, де .

Обчислення маси неоднорідного стержня.

За означенням, лінійна густина неоднорідного стержня дорівнює похідній функції т = т(l), що виражає масу стержня як функцію його довжини.

Отже, = т'(l), тобто функція т = т(l) є

первісною для = (l). Звідси випливає, що масу

стержня на відрізку [l₁;l₂] можна обчислити за

формулою .

Приклад 16. Знайти масу стержня зав­довжки

35 см, якщо його лінійна густи­на змінюється

за законом .

Розв'язання.

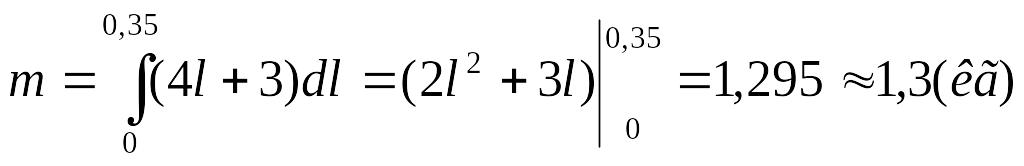
Обчислення кількості електрики.

За означенням, сила стру­му є похідною від кількості електрики Q=Q(t,) де t — час, тобто I(t) = Q'(t). А тоді функція Q = Q(t) є первісною для функції I = I(t)?, тому кількість електрики, що проходить че­рез поперечний переріз провідника за час від t₁ до t₂, можна

знайти за формулою .

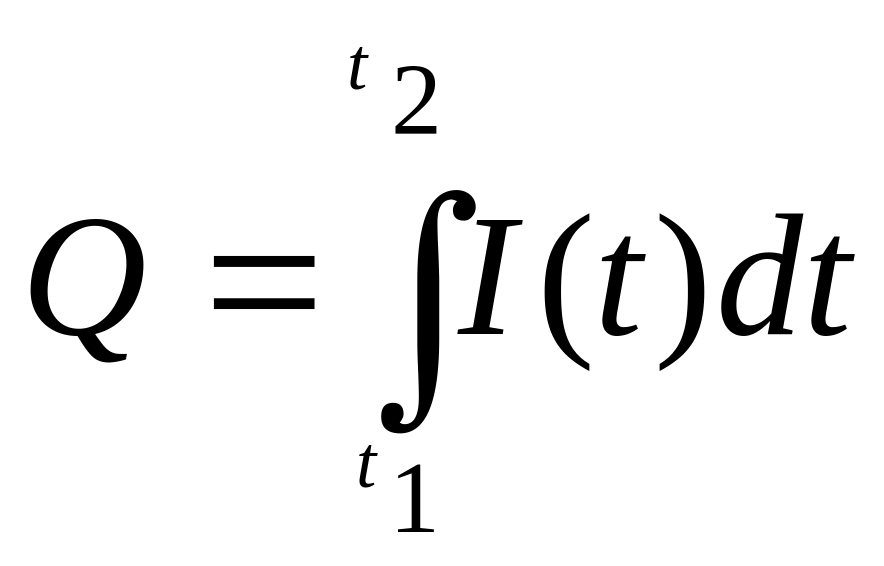За значенням , сила струму є похідною від кількості електрики Q=Q(t), де t – час , тобто .А тоді функція Q= Q(t) є первинною для функції f=f(x) , тому кількість електрики , що проходить через переріз провідника за час , можна знайти за формулою .

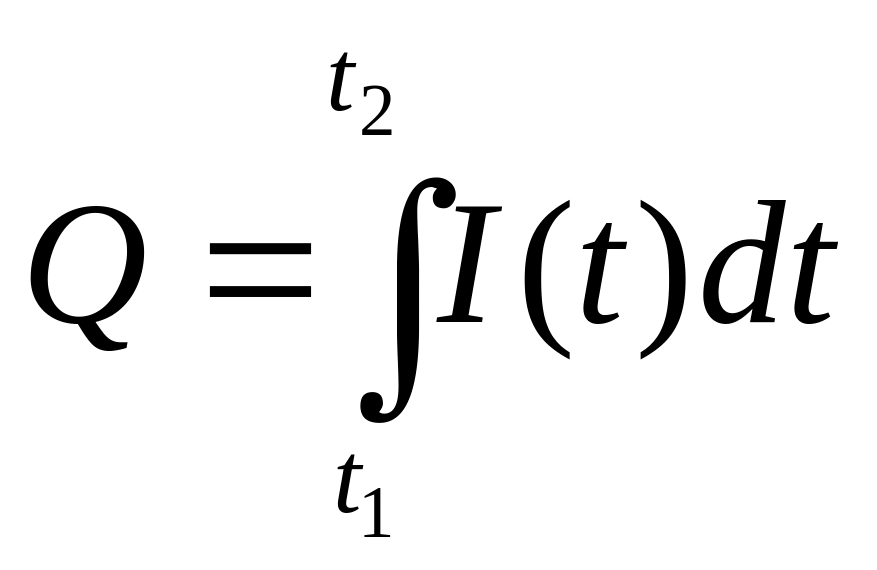Приклад 17. Знайдіть кількість електрики , що проходить через поперечний переріз дроту за 10 с, якщо сила струму змінюється за законом а.

Розв'язання

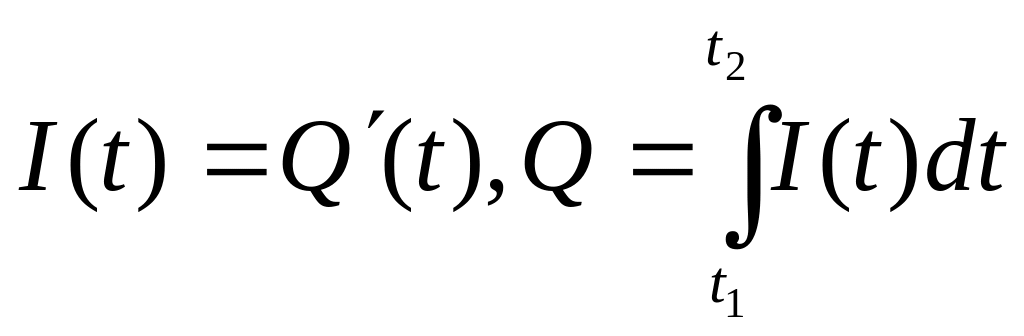, Кл.

Відповідь.210 Кл

Приклад 18. Знайти кількість електрики, що проходить через поперечний переріз провідника за 10 с, якщо сила стру­му змінюється за законом I(t) = (4t + 1)(A).

Розв'язання.

.

Визначений інтеграл широко застосовують під час розв'язування фізико-технічних задач різного характеру, а також задач економічного змісту.

Приклад 19. Експериментально встановлено, що продук­тивність праці робітника наближено виражається формулою

.

де t – робочий час у годинах. Обчислити обсяг випуску продукції за квартал, вважаючи робочий день восьмигодинним, а кількість робочих днів у кварталі – 62.

Розв'язання.

Обсяг випуску продукції протягом зміни є первісною від функції, що виражає продуктивність праці.

Тому

.

Протягом кварталу обсяг випуску продукції становитиме:

Приклад 20. Експериментально встановлено, що залежність затрати бензину автомобілем від швидкості на 100 км шляху визначається формулою Q=- 18 - 0,3u + 0,003u², де . Визначити середню затрату бензину, якщо швидкість руху 50—60 км/год.

Розв'язання.

Середня затрата бензину становить:

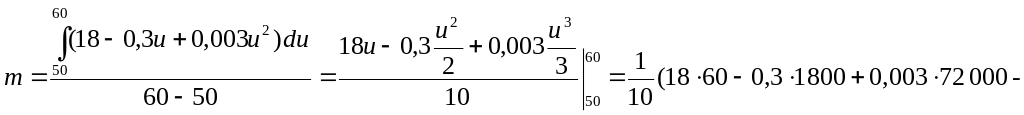
Отже, автомобіль на 100 км шляху, рухаючись зі швидкі­стю 50 — 60 км/год, затрачає в середньому 10,6 л бензину.

Лекція. Наближені методи обчислення визначених інтегралів.

План вивчення теми

1. Формула прямокутників.

2. Формула трапецій.

3. Формула параболічних трапецій (Формула Симпсона).

4. Розвязування прикладів.

Домашнє завдання: індивідуальні завдання (30 варіантів)

Формули прямокутників.

;

.

Формула трапеції:

.

Формула параболічних трапецій (формула Сімпсона):

Приклад 1. Обчислити за допомогою формули Сімпсона , прийняв n =2.

Розв’язання:

.

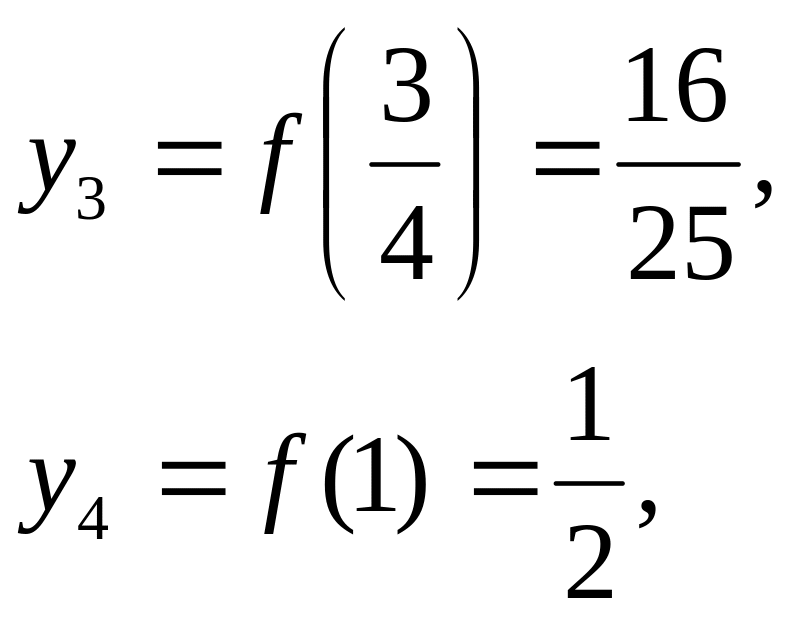Тому що то

.

Точне значення інтегралу є ; відносна похибка %.

Приклад 2.Застосовуючи формулу прямокутників (n = 10), наближено обчислимо (розрахунки вестимемо з трьома знаками після коми). Оцінити похибку наближення.

Розв’язання.

Розіб’ємо відрізок [1;2] на 10 рівних частин точками ( ).Обчислимо значення підінтегральної функції у вибраних точках. Результат запишемо в таблицях.

Хі	1	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2
Уі	1,0	0,909	9,833	0,769	0,714	0,667	0,625	0,588	0,556	0,526	0,5

Дістанемо , маємо .

Оцінюємо похибку наближення. Оскільки , то монотонно спадає на відрізку [1;2]. Тому . Отже, .

Оскільки допустима похибка з’являється вже на другому знаку після коми, третій знак слід округлити, остаточно маємо .

Обчислимо точно даний інтеграл за формулою Ньютона – Лейбніца:

.

Допущена похибка 0,03.

Приклад 3. Застосовуючи формули прямокутників, трапеції, Сімпсона (n = 10), наближено обчислимо .

За формулою прямокутників:

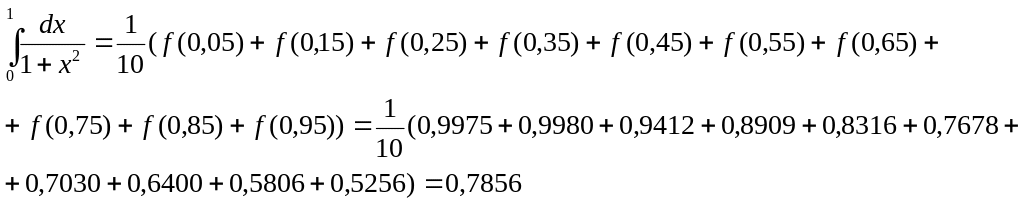
За формулою трапецій:

За формулою Сімпсона:

Точне значення цього інтегралу .

Приклад 4. Для даного інтеграла оцінити похибку за формулою прямокутників із кроком .

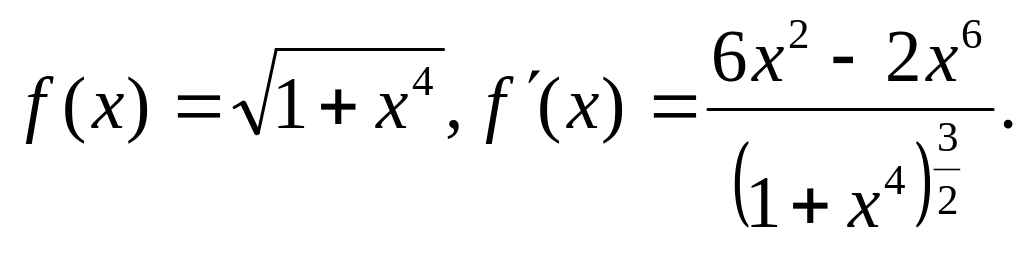Маємо Отже, . Використовуючи похибку для формул прямокутників, дістанемо .

Приклад 5. Знайти крок h, при якому похибка при наближеному обчисленні інтеграла за формулою Сімпсона не перевищуючи , .

Маємо . .Оскільки Враховуючи, що в формулі Сімпсона , з похибки цієї квадратурної формули дістаємо , звідки .

Для визначення кроку у формулі трапеції оцінимо .

і , бо

Використаємо формулу для похибки методу трапецій. Дістанемо ,отже, Тоді за формулою трапецій маємо

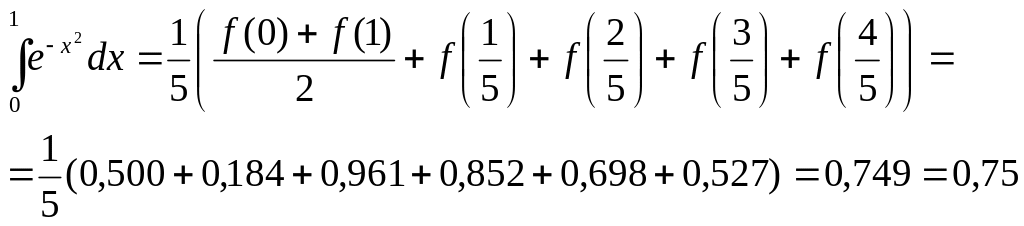
Приклад 6. Користуючись подвійним прорахунком, оцінити похибку результату обчислення інтеграла із заданим кроком за формулою Сімпсона.

Обчислення заданого інтеграла за формулою Сімпсона із кроком , дає результат , а з кроком маємо . Отже, похибка обчислень , і за формулою маємо .