5 . Фігура обмежена графіками трьох і більш неперервних на відрізку функцій.

У цьому випадку намагаються шукати площу представити у виді алгебраїчної суми площ, обчислення кожної з який зводиться до одному з попередніх випадків.

Так, наприклад, площа фігури , зображеної на мал. 8, обчислюється по чи формулі

. (4)

Приклад 5. Обчислити площа плоскої фігури, обмеженої лініями

(мал. 9)

∆ З мал. 9 видно, що шукана площа

чи

▲

Приклад 6. Обчислити площу фігури, обмеженої: 1) синусої­дою у = sin х і відрізком [0; ] осі Ох (мал. 42); 2) кубічною параболою у = х³, віссю Ох та прямими х = 2 і х = 5 (мал. 43).

Р о з в ’ я з а н н я.

1) S = sin xdx = - cos x = - (cos – cos0 ) = - (- 1 - 1) = 2 (кв.од.)

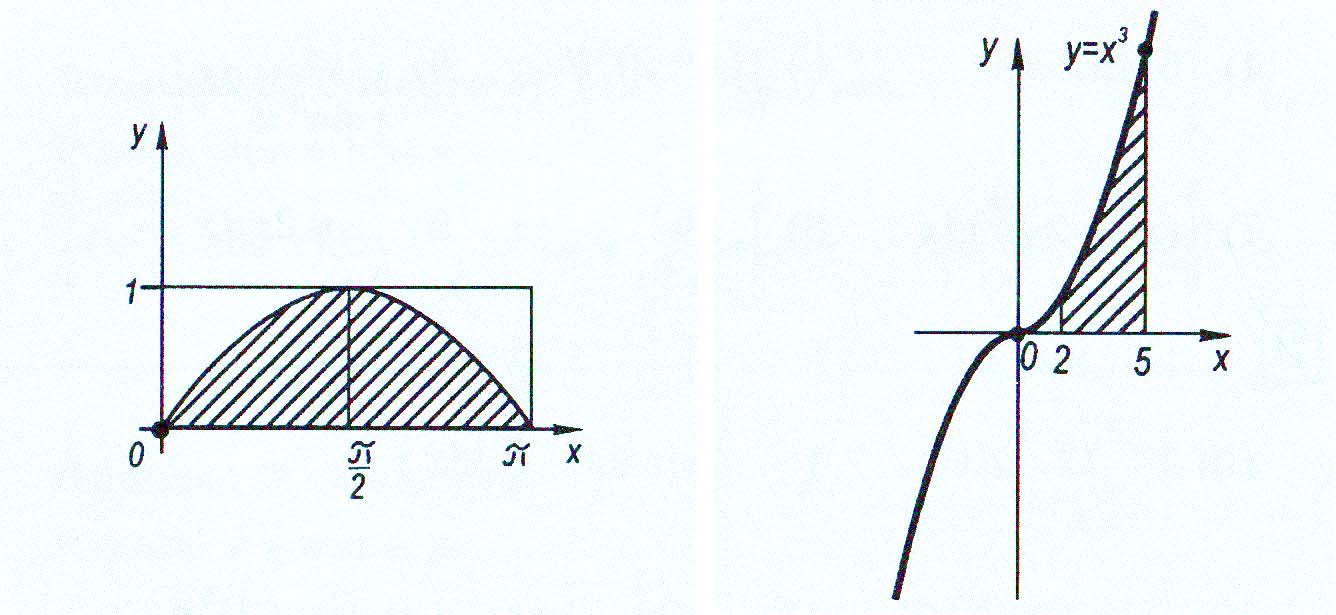
Мал. 42 Мал. 43

2) S = = (5⁴-2⁴) = (5²+2²) (кв.од.).

Виникає запитання, як обчислити площу фігури, обмеженої графіками двох неперервних функцій y=f(x) і y = φ(х) (мал. 44)

Неважко помітити, що S_A1ABB1= ,за першою властивістю інтеграла.

Приклад 6. Обчислити площу фігури, обмеженої кривими у = X² і y = X³.

Р о з в ’ я з а н н я.

Побудувавши ескізи графіків функцій (мал. 45), з'ясуємо, площу якої фігури слід знайти, графіки яких функцій її обмежують і визначимо межі інтегрування.

У даному випадку f(x) = x², φ(x) = x³, a = 0, b = 1.

Чи можна застосувати формулу , якщо фігура, площу якої треба обчислити, розміщена частково чи повністю під віссю Ох (мал. 46).

Щоб переконатися в цьому, досить пере­нести дану фігуру паралельно вздовж осі Оу на відстань т так, щоб вона розмістилася над віссю Ох (мал. 47).

А таке перетворення означає, що дані функції y = f(x) і y = φ(x) ми замінили на нові функції f₁{x) = f(x) + m і φ₁ = φ(x) + m. Площа фігури, обмеженої графіками цих функцій, дорівнює площі даної фігури.

Тому шукана площа

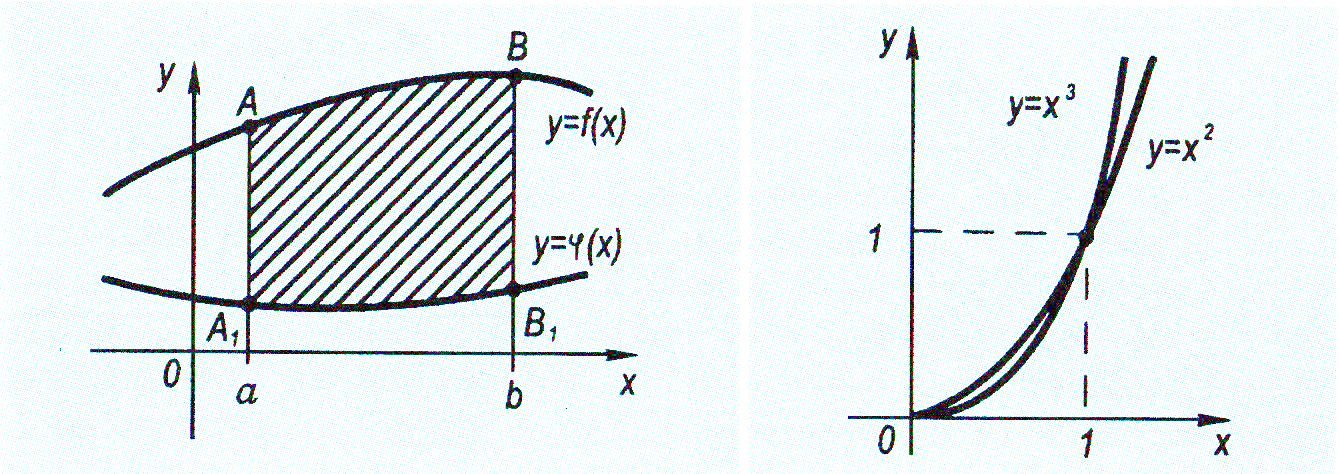
Мал. 44 Мал. 45

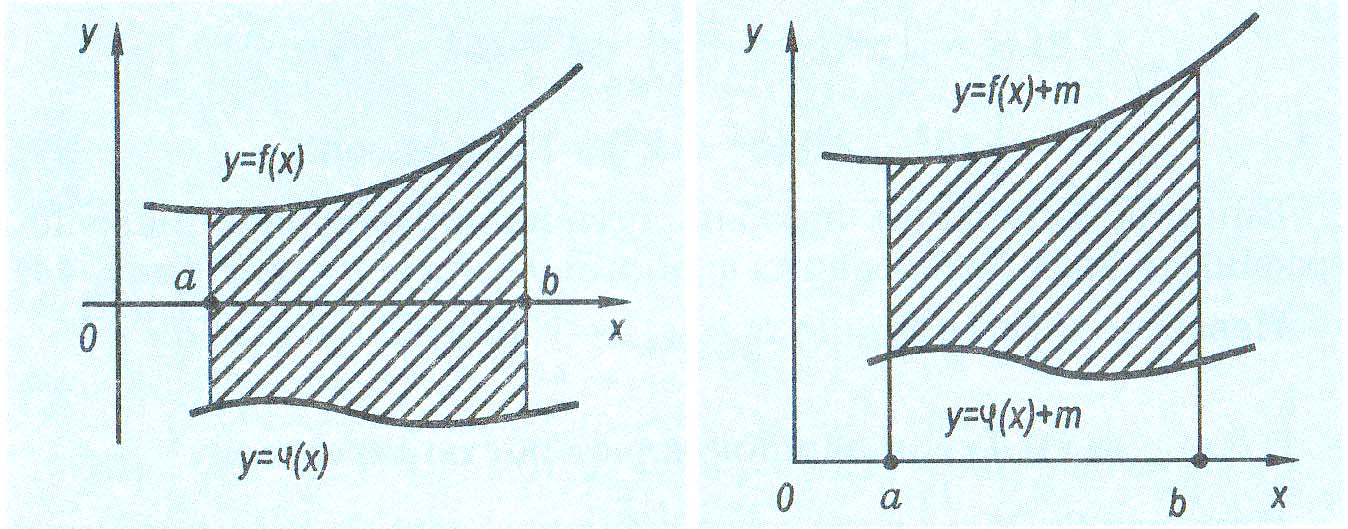
Мал. 46 Мал. 47

Якщо позначити f(x) – φ(x) = q(x), то S = q(x)dx.

Це означає, що для обчислення площі важливої є не форма фігури, а довжина відрізка q(x) ординати, що дорівнює різниці ординат точок графіків відповідних функцій y = f(x) і y= φ(x).

Отже, якщо взяти дві інші функції у = f₁(x) і у = φ₁(x), які задовольняють умови f₁(x) – φ₁(x) = q(x) у будь-якій точці х [а;b], то площа фігури, обмеженої графіками цих функцій, дорівнюватиме площі фігури, обмеженої графіками функцій y = f(x) i y = φ(x) (мал. 48).

Приклад 7. Знайти площу фігури, обмеженої параболою у = 4 – х² та прямими (мал. 49).

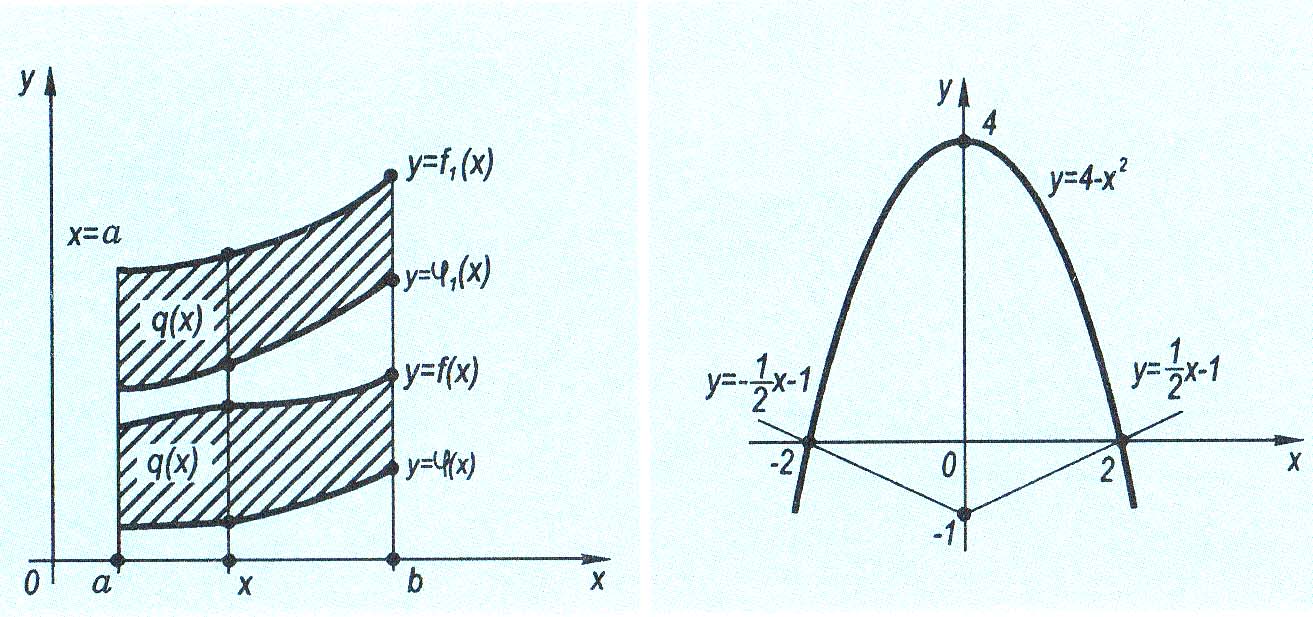
Мал. 48 Мал. 49

Р о з в ’ я з а н н я.

На відрізку [-2,0]

а на відрізку [-2;0]

Шукану площу знаходимо як суму двох визначених інтегралів:

(кв.од.).

Площа даної фігури можна обчислити раціональніше, якщо звернути увагу на те, що фігура симетрична відносно осі Оу.

Тому

(кв.од.).

Зазначимо, що коли криволінійна трапеція розміщена під віссю Ох (мал. 50), то - від’мний. Тоді вважатимемо, що S =

Обчислення об’єму тіла по відомих площах його поперечних переріз.

Нехай потрібно обчислити обсяг V тіла, укладеного між двома перпендикулярними до осі Ох площинами х = а, х = b (мал. 10).

П рипустимо, що відомо площу будь-якого перетину тіла площиною, перпендикулярної до осі Ох.

Ця площа залежить від положення січної площини, тобто є функцією від х. Позначимо її через S(x) і допустимо, что вона неперервна на відрізку [a; b].

Розіб'ємо відрізок [a; b] на n частин тачками

і через точками розподілу проведемо площини, перпендикулярні до осі Ох.

Ці площини розіб'ють тіло на n шарів. Позначимо через обсяг слоя, ув'язненого між площинами х = х_i-1 і х = х_i. Тоді V_i приблизно дорівнює обсягу циліндра, висота якого дорівнює , а підстава збігається з поперечним перерізом, утвореним перетинанням тіла якою-небудь площиною

По визначенню маємо (1)