1. Визначений інтеграл і його геометричний зміст.

Нехай функція F(x) є первісної для функції f(x) у деякому проміжку Х, а числа a і b належать цьому проміжку.

Приріст F(b) – F(a) кожної з первісних функцій (x) + C при зміні аргументу від х = а до х = b називається означеним інтегралом від а до b функції f(x) і позначається (читається: « інтеграл від а до b еф від ікс де ікс»).

Числа а і b називаються границями інтегрування, а – нижньою, b – верхньою. Відрізок називається підінтегральною функцією, а змінна х – змінної інтегрування.

Нехай дана функція f(x), визначена на відрізку , де а<b. Виконаємо наступні операції:

1. розіб'ємо відрізок на n частин точками х 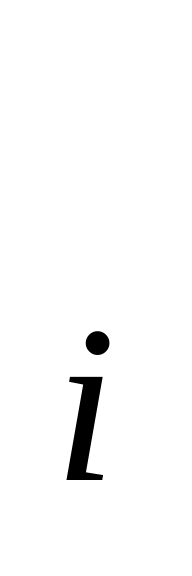( i = 0, 1, 2, …, n) так щоб

а = х <x ;

2. позначимо: 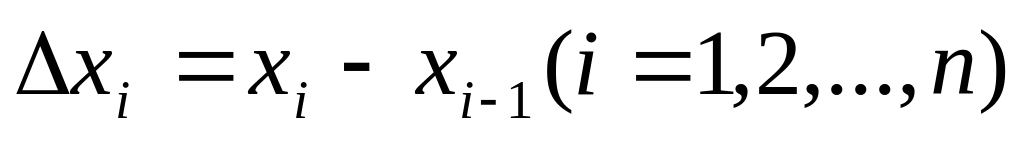; величину 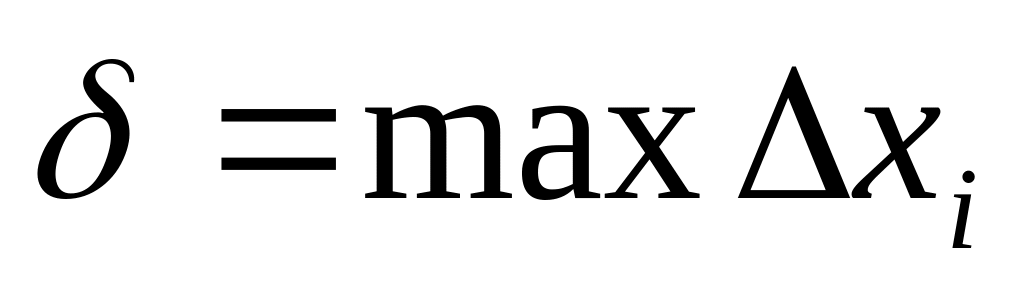назвемо кроком розбивки.

3. у кожнім з відрізків 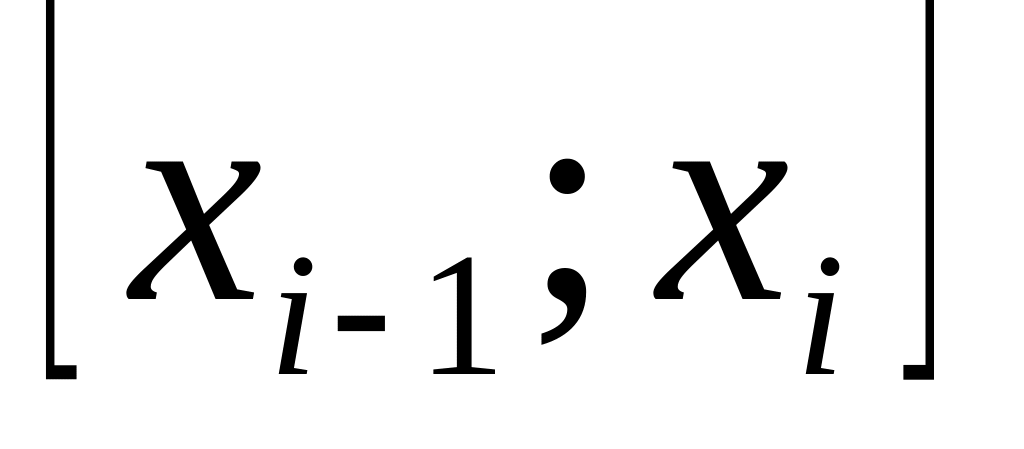зафіксуємо довільну точку 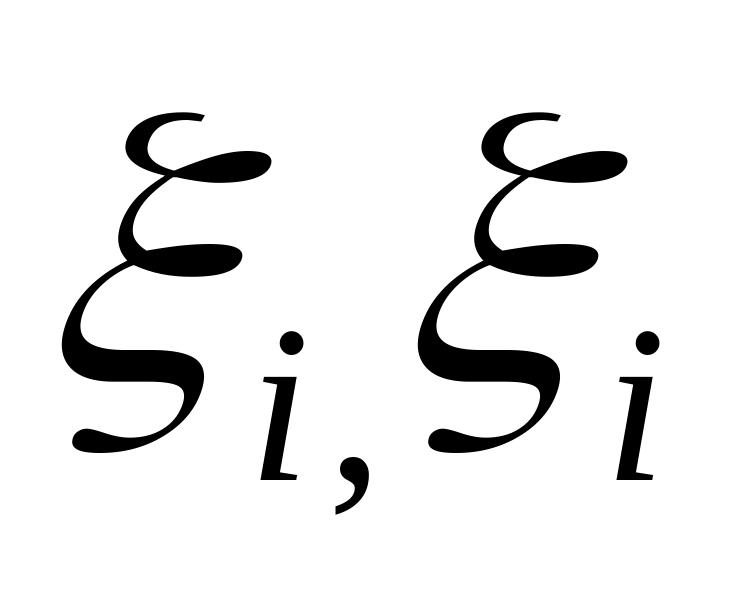Є ;

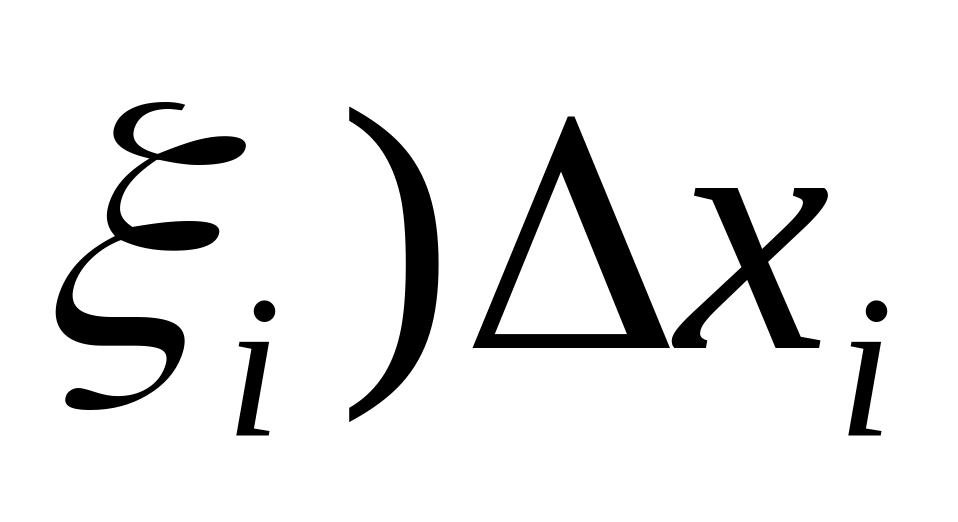4. складемо суму Q усіх добутків f( (i= 1 ,…,n):

Q ,

Або, у скороченому вигляді,

Q (14.)

Суми вигляду (14.) називаються інтегральними сумами функції f(x). Якщо функція f(x) додатня на , площі прямокутника з основою довжини і з

висотою . А вся сума Q дорівнює площі « східчастої фігури», що

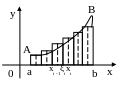
виходить об'єднанням усіх зазначених вище прямокутників (мал.2).

При різних розбивках відрізка на частині одержимо різні

інтегральні суми виду (14) , отже і різні «східчасті фігури». Таким чином, для даної функції f(x) і даного відрізка можна скласти нескінченна безліч інтегральних сум виду (14), що залежать від числа n і від вибору точок розподілу х і точок .

Якщо при будь-якій послідовності розбивок відрізка таких, що і при будь-якому виборі точок інтегральна сума прагне до тої самої кінцевої межі А:

те число А називається означеним інтегралом від функції f(x) на відрізку і позначається .

Отже, по визначенню

. (15).

Функція f(x), для якої існує означений інтеграл (15), називається інтегрованою на відрізку .

Усяка неперервна на відрізку функція f(x) інтегрована на цьому відрізку.

Геометричний зміст означеного інтеграла полягає в тім, що: якщо функція, що інтегрується на відрізку, f(x) ненегативна, чисельно означений інтеграл чисельно дорівнює площі S криволінійної трапеції, обмеженої графіком функції f(x), віссю абсцис і прямими х=а і , х=b, тобто

.

Означений інтеграл залежить тільки від функції, що інтегрується, f(x) і меж інтегрування а і b, але і від того якою літерою позначається змінна інтегрування. Тому

(16).

і т.д.

Відповідно до визначення (6) означений інтеграл є межа інтегральної суми, число членів якої необмежено зростає, а кожен доданок прагне до нуля. Зі шкільного курсу, звісно. Що рішення ряду задач зводиться до обчислення меж інтегральних сум виду (14). Цим мотивується необхідність уведення визначення 6.