2. Інтегруюча ланка з затримкою.

Диференційне рівняння:

Передаточна функція:

Цю ланку можна уявити як сукупність послідовно ввімкнутих ланок – ідеальної інтегруючої та аперіодичної першого порядку:

перехідна функція вагова функція

(t)

T

t

0

АФЧХ АЧХ ФЧХ

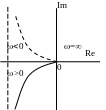
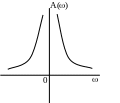
3. Ізодромна ланка.

Диференційне рівняння:

Передаточна функція:

де Т=к₁/к

Ланку можна уявити як сукупність двох ланок, що діють паралельно – ідеально інтегруюча та безінерційна.

(Приклад: гідравлічний демпфер з пружиною)

п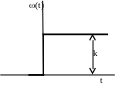 ерехідна функція вагова функція

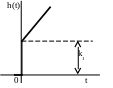
h(t)=(kt+k₁)1(t) (t)=k1(t)+k₁(t)

А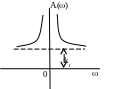 ФЧХ АЧХ ФЧХ

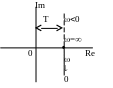
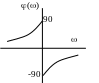
Дана ланка має властивості вводити інтегруючу дію в області малих частот, що покращує якісні показники систем автоматичного регулювання.

в) диференціююча ланки

1.Ідеальна диференціююча ланка

Диференційне рівняння:

Передаточна функція:

W(p)=kp

(Приклад: тахогенератор, операційний підсилювач в режимі диференціювання)

перехідна функція вагова функція

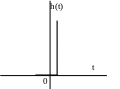
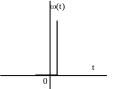
h(t)=k(t)

При t=0 буде миттєвий стрибок від 0 до  і знову повернення до 0

АФЧХ АЧХ ФЧХ

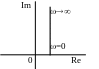
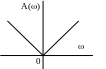
Диференціююча ланка найкраще пропускає високочастотні коливання вхідної величини. Всі її характеристики протилежні характеристикам інтегруючої ланки.

2. Диференціююча ланка з затримкою (реальна диференцююча ланка)

Диференційне рівняння:

Передаточна функція:

або

Модуль . Кут зсуву

Ланку можна уявити як дві ввімкнуті послідовно ланки – ідеально диференціюючу та аперіодичну першого порядку.

(Приклад: RC-ланцюг, трансформатор)

перехідна функція вагова функція

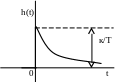
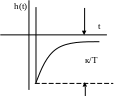
АФЧХ АЧХ ФЧХ

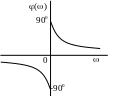
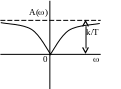
В області високих частот реальна ланка пропускає сигнал гірше ніж ідеальна

Фазове зміщення є найбільшим при низьких частотах. На високих частотах кут зменшується і наближається до0 при



г) трансцендентні ланки – описується неалгебраїчними передаточними функціями. До них відносять ланки чистого запізнення.

(Приклад: живильник з транспортером, магнітний запис та відтворення сигналів, електроланцюг з розподіленими параметрами)

x₂(t)=x₁(t-)   0

Передаточна функція:

або

перехідна функція вагова функція

h(t)=1(t-) (t)=(t-)

АФЧХ АЧХ ФЧХ

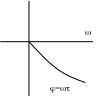
Коло одиничного вектора. Ланка відтворює коливання будь-якої частоти без викривлення, але з відставанням за фазою, яке залежить від частоти.

A() = 1 ()= -T