0. 1.2.3 Перехідна функція

Для порівняння динамічних властивостей різних елементів системи, розгляд їх проводять в перехідному процесі при нульових початкових умовах і типових вхідних діях.

Під початковими умовами розуміють значення вихідної величини (і всіх її похідних) в момент t=t₀ при умові, що до цього часу зовнішня дія була відсутня.

В автоматиці використовують типові вхідні дії, що описуються ступінчастими, імпульсними та гармонійними функціями.

а) ступінчаста дія описується одиничною ступінчастою функцією

t при t  0

1(t) =

0 при t  0

Реакція ланки на одиничну ступінчасту функцію називається перехідною функцією і позначається h(t).

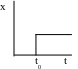
б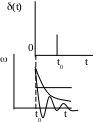 ) імпульсна перехідна функція – описується дельта-функцією Дірка, що є математичною ідеалізацією короткого імпульсу, площа якого дорівнює 1 при його нульовій довжині та нескінченій амплітуді:

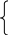 при t = 0

 (t)=

0 при t  0

або

Реакція ланки на імпульсну функцію називається ваговою функцією -  (t).

Між перехідною та ваговою функціями існує зв'язок:

 (t)=dh(t)/dt 

Дані функції відносять до часових характеристик ланок. Описання ланок часовими характеристиками для систем високого порядку ускладнене, що є їх недоліком.

0. 1.2.4 Передаточна функція

Передаточною функцією називається відношення лапласового зображення вихідної величини до лапласового зображення вхідної величини при нульових початкових умовах:

де Q(p) – характеристичний многочлен ланки, а рівняння Q(p)=0 –називається характеристичним рівнянням.

Корені рівняння Q(p)=0 називаються полюсами передаточної функції.

Корені рівняння Р(p)=0 називаються нулями передаточної функції.

Описання системи при прикладенні гармонійної вхідної дії – проводиться частотними характеристиками. При проходженні гармонійного сигналу через ланку, він викликає її реакцію, що в усталеному режимі також описується гармонійною функцією з тією ж частотою, але із зміненою амплітудою та фазою коливань по відношенню до вхідного збурення.

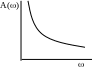
Амплітудночастотна характеристика (АЧХ) – відношення амплітуди вихідної величини до амплітуди вхідної величини в залежності від частоти:

Фазочастотна характеристика (ФЧХ) – різниця фаз коливань в залежності від частоти:

 () = ₂ - ₁.

Амплітудно-фазова частотна характеристика (АФЧХ) – геометричне місце кінців векторів амплітуд передаточної функції при зміні частоти від нуля до нескінченності (годограф).

Частотні характеристики ланок залежить тільки від їх властивостей, але не залежить від амплітуди та фази вхідних гармонійних сигналів.

Для виявлення зв’язку характеристиками та диференційним рівнянням ланки, вхідні та вихідні величини подаються в комплексній формі.

Частотна перехідна функція:

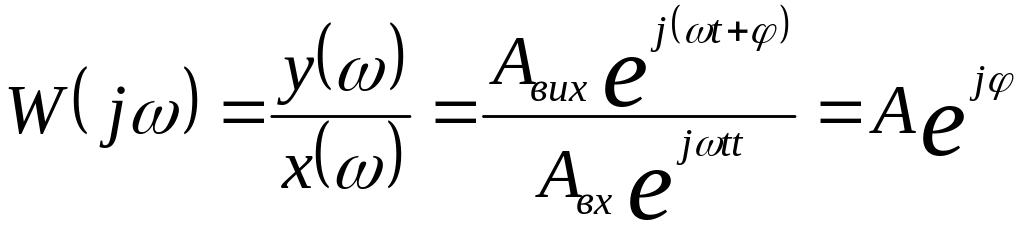
або W(j) = P() + jQ()

Модуль частотної передаточної функції:

Аргумент (кут зміщення):

tg =Q()/P()   =arctg( Q()/P())

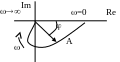
АФЧХ

АЧХ

ФЧХ