2.6 Аналіз нелінійних систем автоматичного керування

2.6.1 Загальні поняття нелінійних систем

Нелінійними називаються автоматичні системи, динаміка руху яких описується нелінійними диференційними рівняннями. Нелінійність диференційних рівнянь обумовлена нелінійною характеристикою елементів системи. Якщо в системі є хоча б одна ланка з нелінійною статичною характеристикою, то вся система буде нелінійною.

Динамічні характеристики нелінійних елементів описуються нелінійними диференційними рівняннями, точне інтегрування яких, як правило, неможливе.

Майже всі реальні елементи автоматичних систем нелінійні і лише наближено їх вважають лінійними.

Не лінійності розбивають на дві групи: несуттєві та суттєві.

До першої відносять такі не лінійності, на яких при малому діапазоні зміни аргументу, вибирають ділянки близькі до лінійних і заміняють їх лінійними ділянками. Динамічні розрахунки таких систем ведуть як для лінійних.

До других відносять не лінійності, що бувають розривними або неоднозначними функціями, або функціями, що мають злам:

а) нечутливість – при зростанні вхідного сигналу х_вх за модулем в один чи інший бік від нуля до деякого значення  а, цей сигнал через нелінійний елемент не проходить.

С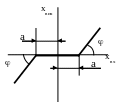 татична характеристика:

х_вих = 0 при х_вх а

х_вих = k (х_вх – a) при х_вх  а

х_вих = k (х_вх + a) при х_вх  - а

k=tg - коефіцієнт пропорційності.

Величина 2а називається зоною нечутливості елемента.

Приклад: механічний підсилювач

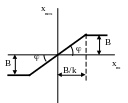
б) обмеженість – вихідна величина не може перевищувати за модулем певну межу В.

Статистична характеристика:

х_вих = k х_вх при х_вх B/k

х_вих =B при х_вх  B/k

х_вих = -B при х_вх  -B/k

Приклад: мембрана чутливого елементу, електричний підсилювач.

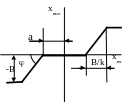
в) нечутливість і обмеження.

С татична характеристика:

х_вих = 0 при х_вх а

х_вих = k (х_вх – a) при а х_вх  B/k+ а

х_вих =B при х_вх  B/k + а

х_вих = k (х_вх + a) при -(B/k+а)  х_вх  - а

х_вих = -B при х_вх  -(B/k +а)

Приклад: гідравлічний та пневматичний підсилювачі

г) люфт

С татична характеристика:

х _вих = k (х_вх - a) при dx_вх /dt  0

та k х_вх – х_вих= kа

х_вих = k (х_вх + a) при dx_вх /dt 0

та х_вих - k х_вх = kа

dx_вх /dt =0 при  k х_вх – х_вих kа

k=tg

Приклад:механічні передачі з зазором.

д) люфт з обмеженням

С татична характеристика:

х _вих = k (х_вх - a) при dx_вх /dt  0, k х_вх – х_вих= kа

та -(B/k - а)  х_вх  B/k + а

х_вих =B при dx_вх /dt  0 та х_вх  B/k + а

х_вих = -B при dx_вх /dt  0 та х_вх  - (B/k – а)

х_вих = k (х_вх + a) при dx_вх /dt  0, х_вих- k х_вх = kа

та -(B/k + а)  х_вх  B/k – а

х_вих =B при dx_вх /dt  0 та х_вх  B/k – а

х_вих = -B при dx_вх /dt  0 та х_вх  - (B/k + а)

dx_вх /dt =0 при  k х_вх – х_вих kа

та х_вх  B/k + а

е) релейні елементи – вихідна величина може приймати лише кінцеве число значень при безперервній зміні вхідної величини:

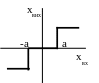- релейний елемент з зоною нечутливості;

х _вих = 0 при -а х_вх  а

х_вих =B при х_вх  а

х_вих = -B при х_вх  - а

• р 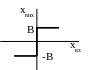елейний елемент без зони нечутливості;

- з нейтральним положенням:

х _вих = 0 при х_вх = 0

х_вих =B при х_вх  0

х_вих = -B при х_вх  0

- без нейтрального положення:

х _вих =B при х_вх  0

х_вих = -B при х_вх  0

• н еоднозначний релейний елемент без зони нечутливості;

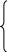х _вих =B при х_вх  b

х_вих = -B при х_вх  b

х_вих =B при dx_вх /dt  0 та -b х_вх  b

х_вих = -B при dx_вх /dt  0 та -b х_вх  b

Величина 2bвизначає величину зони неоднозначності.

• н еоднозначний релейний елемент з зоною нечутливості;

х _вих =B при х_вх  а₂

х_вих = -B при х_вх  - а₁

х_вих =0 при – а₁  х_вх  а₁

х_вих =В при – а₁  х_вх  а₂ та dx_вх /dt  0

х_вих =0 при а₁  х_вх  а₂ та dx_вх /dt  0

х_вих = -В при –а₂ х_вх  - а₁ та dx_вх /dt  0

х_вих =0 при – а₂  х_вх  а₁ та dx_вх /dt  0